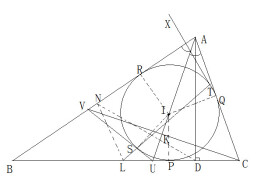
費爾巴哈定理
費爾巴哈定理
三角形的九點圓與其內切圓以及三個旁切圓相切。
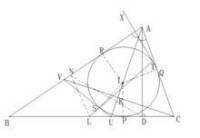
全局圖
假設與相切於點,那麼LT與相交,設另一個交點為。
過點作的切線,分別交和於,連接。
又作兩圓的公切線,使其與邊位於的同側。
由假設知
而和都是的切線,且與弦所夾的圓弧相同,於是
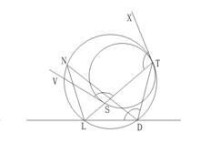
局部圖1
則
這就是說,共圓。
而這等價於:
又
故有
另一方面,是公共的切點,自然在上,
因此共圓,進而有
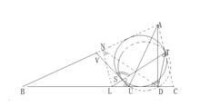
局部圖2
而
(這裡用了,以及直角三角形斜邊上中線等於斜邊的一半)
所以,就得到
注意到均與相切,於是有
三式相加,即知
也即是說三點共線。
另外,,這可由得到。
(這說明,公切點可如下得到:
連接,並延長交於點,
過點作的切線,切點為,交於,
最後連接,其延長線與的交點即是所謂的公切點。
連接,與交於點,
則是的中點。
前面已得到:
而
即
然而
是的中位線
於是
因之
故
由於以上推導均可逆轉,因此我們只需證明:。往證之
這等價於:與圓相切
於是只需證:
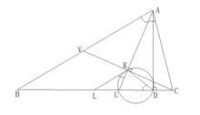
局部圖3
又是角平分線,於是
於是又只需證:
即證:
這即是證:四點共圓
由於(易得),
所以確實共圓。
這就證明了與內切。
旁切圓的情形是類似的。
證畢
另略證:
(其中是垂心H的垂足三角形的內切圓半徑,是三角形外接圓和內切圓半徑)
這就證明了九點圓與內切圓內切(九點圓半徑為外接圓半徑一半。是九點圓圓心,為內心)