切比雪夫濾波器
切比雪夫濾波器
切比雪夫濾波器，又名“車比雪夫濾波器”，是在通帶或阻帶上頻率響應幅度等波紋波動的濾波器。切比雪夫濾波器來自切比雪夫分佈，以“切比雪夫”命名，是用以紀念俄羅斯數學家巴夫尼提·列波維其·切比雪夫（Пафнутий Львович Чебышёв）。
根據頻率響應曲線波動位置的不同，切比雪夫濾波器可以分為以下兩種：
在通帶（或稱“通頻帶”）上頻率響應幅度等波紋波動的濾波器稱為“I型切比雪夫濾波器”；
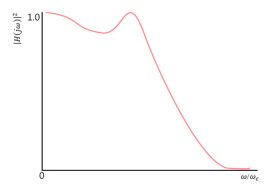
'''n'''階第一類切比雪夫濾波器的幅度與頻率的關係可用下列公式表示
：:
其中：
*
*而
是濾波器在截止頻率的放大率 (''注意'': 常用的以幅度下降3[[分貝]]的頻率點作為截止頻率的定義不適用於切比雪夫濾波器!)
f>：> 是 n階切比雪夫多項式
其中
或:
'''切比雪夫濾波器'''的階數等於此濾波器的電子線路內的電抗元件數。
切比雪夫濾波器的幅度波動 =分貝
當,切比雪夫濾波器的幅度波動= 3分貝。
切比雪夫多項式在逼近理論中有重要的應用。這是因為第一類切比雪夫多項式的根（被稱為切比雪夫節點）可以用於多項式插值。相應的插值多項式能最大限度地降低龍格現象，並且提供多項式在連續函數的最佳一致逼近。
| 切比雪夫多項式 | |
|---|---|
| n | 切比雪夫多項式 |
| 1 | 1 |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
在阻帶（或稱“阻頻帶”）上頻率響應幅度等波紋波動的濾波器稱為“II型切比雪夫濾波器”。
也稱倒數切比雪夫濾波器，較不常用，因為頻率截止速度不如I型快，也需要用更多的電子元件。II型切比雪夫濾波器在通頻帶內沒有幅度波動，只在阻頻帶內有幅度波動。
II型切比雪夫濾波器的轉移函數為：
分貝
5分貝衰減度相當於 ; 10分貝衰減度相當於。
-3分貝頻率 和截止頻率 有如下關係：
基本信息
- 外文名
- 俄文：Пафнутий Львович Чебышёв 英文：Chebyshev
- 來源
- 切比雪夫分佈
- 性質
- 濾波器