直角三角形

直角三角形如圖所示：分為兩種情況，有普通的直角三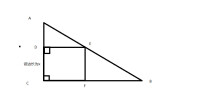角形，還有等腰直角三角形（特殊情況)在直角三角形中，與直角相鄰的兩條邊稱為直角邊，直角所對的邊稱為斜邊。直角三角形直角所對的邊也叫作“弦”。若兩條直角邊不一樣長，短的那條邊叫作“勾”，長的那條邊叫作“股”。

等腰直角三角形是一種特殊的三角形

等腰直角三角形是一種特殊的三角形，具有所有三角形的性質：具有穩定性、內角和為180°。兩直角邊相等，兩銳角為45°，斜邊上中線、角平分線、垂線三線合一，等腰直角三角形斜邊上的高為此三角形外接圓的半徑R。

它除了具有一般三角形的性質外，具有一些特殊的性質：

1、直角三角形兩直角邊的平方和等於斜邊的平方。如圖，（勾股定理)

2、在直角三角形中，兩個銳角互余。如圖，若

3、直角三角形中，斜邊上的中線等於斜邊的一半（即直角三角形的外心位於斜邊的中點，外接圓半徑R=C/2）。該性質稱為直角三角形斜邊中線定理。

4、直角三角形的兩直角邊的乘積等於斜邊與斜邊上高的乘積。

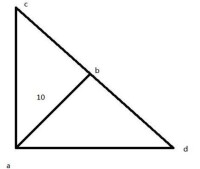
5、如圖，Rt△ABC中，，AD是斜邊BC上的高，則有射影定理如下：

（1）。

（2）。

（3）。

射影定理，又稱“歐幾里德定理”：在直角三角形中，斜邊上的高是兩條直角邊在斜邊射影的比例中項，每一條直角邊又是這條直角邊在斜邊上的射影和斜邊的比例中項。是數學圖形計算的重要定理。

6、在直角三角形中，如果有一個銳角等於30°，那麼它所對的直角邊等於斜邊的一半。

在直角三角形中，如果有一條直角邊等於斜邊的一半，那麼這條直角邊所對的銳角等於30°。

證明方法多種，下面採取較簡單的幾何證法。

先證明定理的前半部分，Rt△ABC中，

∵

∴（直角三角形兩銳角互余）

取AB中點D，連接CD，根據直角三角形斜邊中線定理可知

∴△BCD是等邊三角形（有一個角是60°的等腰三角形是等邊三角形）

∴

再證明定理的後半部分，Rt△ABC中，

取AB中點D，連接CD,那麼（直角三角形斜邊上的中線等於斜邊的一半）

又∵

∴

∴

∴

7、如圖，

在Rt△ABC中，AD是斜邊上的高，則：

證明：

兩邊乘以2，再平方得

運用勾股定理，再兩邊除以 ,最終化簡即得

性質8:直角三角形被斜邊上的高分成的兩個直角三角形和原三角形相似。

判定1：有一個角為90°的三角形是直角三角形。

判定2：若，則以a、b、c為邊的三角形是以c為斜邊的直角三角形（勾股定理的逆定理）。

判定3：若一個三角形30°內角所對的邊是某一邊的一半，則這個三角形是以這條長邊為斜邊的直角三角形。

判定4：兩個銳角互為餘角（兩角相加等於90°）的三角形是直角三角形。

判定5：若兩直線相交且它們的斜率之積互為負倒數，則兩直線互相垂直。那麼這個三角形為直角三角形。

判定6：若在一個三角形中一邊上的中線等於其所在邊的一半，那麼這個三角形為直角三角形。參考直角三角形斜邊中線定理

判定7：一個三角形30°角所對的邊等於某一鄰邊的一半，則這個三角形為直角三角形。

判定3和7的證明：

已知△ABC中，，∠A，∠C對的邊分別為a，c，且

證法1：

正弦定理，在△ABC中，有

將a與c的關係及∠A的度數代入之後化簡得

又∵

∴

證法2

反證法，假設，過B作於D

在Rt△ABD中,∵

∴（30°的直角邊等於斜邊的一半）

又∵

∴

但BD是B到直線AC的垂線段，根據垂線段最短可知，從而出現矛盾。

（或從得，那麼△ABC中就有兩個直角，這是不可能的事情）

∴假設不成立，

證法3

利用三角形的外接圓證明

作△ABC的外接圓，設圓心為O，連接OC,OB

∵，A在圓上

∴

∵

∴△BOC是等邊三角形,

又∵

∴AB是直徑

∴(直徑所對的圓周角是直角)

等腰直角三角形的邊角之間的關係：

（1）三角形三內角和等於180°；

（2）三角形的一個外角等於和它不相鄰的兩個內角之和；

（3）三角形的一外角大於任何一個和它不相鄰的內角；

（4）三角形兩邊之和大於第三邊，兩邊之差小於第三邊；

（5）在同一個三角形內，大邊對大角，大角對大邊.

等腰直角三角形中的四條特殊的線段：角平分線，中線，高，中位線.

（1）三角形的角平分線的交點叫做三角形的內心，它是三角形內切圓的圓心，它到各邊的距離相等.

（三角形的外接圓圓心，即外心，是三角形三邊的垂直平分線的交點，它到三個頂點的距離相等）.

（2）三角形的三條中線的交點叫三角形的重心，它到每個頂點的距離等於它到對邊中點的距離的2倍。

（3）三角形的三條高的交點叫做三角形的垂心。

（4）三角形的中位線平行於第三邊且等於第三邊的二分之一。

（5）三角形的一條內角平分線與兩條外角平分線交於一點，該點即為三角形的旁心。

注意：

①任意三角形的內心、重心都在三角形的內部 .

②鈍角三角形垂心、外心在三角形外部。

③直角三角形垂心、外心在三角形的邊上。

（直角三角形的垂心為直角頂點，外心為斜邊中點。）

④銳角三角形垂心、外心在三角形內部。

⑤任意三角形的旁心一定在三角形的外部。

中線：頂點與對邊中點的連線，平分三角形。

角平分線：平分三角形一內角的線段。

高線：三角形中一頂點向對邊作的垂線

勾股定理

如果直角三角形兩直角邊分別為A，B，斜邊為C，那麼即直角三角形兩直角邊長的平方和等於斜邊長的平方。如果三角形的三條邊A，B，C滿足;，還有變形公式： ，如：一條直角邊是a，另一條直角邊是b，如果a的平方與b的平方和等於斜邊c的平方那麼這個三角形是直角三角形。（稱勾股定理的逆定理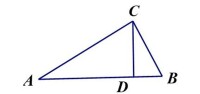）由畢達哥拉斯在公元前550年提出。

如圖1，是屋架設計圖的一部分，點D是斜梁AB的中點

立柱為BC，DE垂直於橫樑AC，，求BC、DE要多長？

解：∵

又

∵點D是AB的中點,

（一）已知兩條直角邊的長度，可按公式：計算斜邊。

（二）如已知一條直角邊和一個銳角，可用直角三角函數計算斜邊。

直角三角形ABC的六個元素中除直角C外，其餘五個元素有如下關係：

例：角A等於30°，角A的對邊是4米，計算斜邊C是多少？

查表

三角函數值除了查表，也可以用電腦系統自帶的計算器，計算。

開始——程序——附件——計算器。這個計算器有兩種模式，點‘查看’有一個下拉菜單，有標準型和科學型，選擇科學型，輸入度數后正弦點sin，餘弦點cos，正切點tan，值就直接顯示出來了。

這裡有一個度和度分秒轉換的問題。如 18.69度，其中整數18就是18°，那麼，用這裡整數41就是41分，再

再用這個24就是秒。

也可以用計算器直接轉換：輸入度數18.69——鉤上Hyp——再點dms

就顯示出18.4124，這就是18度41分24秒。

如要轉換回去就輸入18.4124——鉤上Inv——再點dms,就轉換了。

有一點請注意，顯示度分秒時，小數點後面是一位數或三位數如：

15.3； 15.302，應讀作15度30分；和15度30分20秒。

含義：一般地，直角三角形中，除直角外，共有五個元素，即3條邊和2個銳角，由直角三角形中除直角外的已知元素，求出未知元素的過程，叫做解直角三角形。

1.三條邊的關係：

2.歸納

利用解直角三角形的知識解決實際問題的一般過程：

● ● 將實際問題抽象為數學問題（畫出平面圖形，轉化為解直角三角形的問題）。

● ● 根據條件的特點，適當選用銳角三角形函數等去解直角三角形；

● ● 得到數學問題的答案。

● ● 得到實際問題的答案。