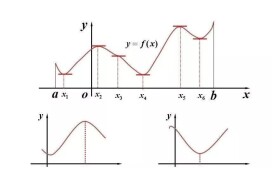
函數最值

一般的，函數最值分為函數最小值與函數最大值。

設函數的定義域為I，如果存在實數M滿足：①對於任意實數，都有，②存在。使得，那麼，我們稱實數M 是函數的最小值。

設函數的定義域為I，如果存在實數M滿足：①對於任意實數x∈I，都有，②存在。使得，那麼，我們稱實數M 是函數的最大值。

一次函數（linear function），也作線性函數，在x,y坐標軸中可以用一條直線表示，當一次函數中的一個變數的值確定時，可以用一元一次方程確定另一個變數的值。所以，無論是正比例函數，即： 。還是普通的一次函數，即： （k為任意不為0的常數，b為任意實數），只要x有範圍，即或（要有意義），那麼該一次函數就有最大或者最小或者最大最小都有的值。而且與a的取值範圍有關係。當時，則y隨x的增大而減小，即y與x成反比。則當x取值為最大時，y最小，當x最小時，y最大。例：則當時，y最小，時，y最大。當時，則y隨x的增大而增大，即y與x成正比。則當x取值為最大時，y最大，當x最小時，y最小。例：則當時，y最大，時，y最小。

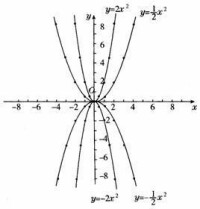
一般地，我們把形如（其中a，b，c是常數，）的函數叫做二次函數（quadratic function），其中a稱為二次項係數，b為一次項係數，c為常數項。x為自變數，y為因變數。等號右邊自變數的最高次數是2。注意：“變數”不同於“未知數”，不能說“二次函數是指未知數的最高次數為二次的多項式函數”。“未知數”只是一個數（具體值未知，但是只取一個值），“變數”可在一定範圍內任意取值。在方程中適用“未知數”的概念（函數方程、微分方程中是未知函數，但不論是未知數還是未知函數，一般都表示一個數或函數——也會遇到特殊情況），但是函數中的字母表示的是變數，意義已經有所不同。從函數的定義也可看出二者的差別。如同函數不等於函數關係。

而二次函數的最值，也和一次函數一樣，與a扯上了關係。當a<0時

觀察右圖。當時，則圖像開口於，一樣，則此時y 有最大值，且y只有最大值（聯繫圖像和二次函數即可得出結論），此時y值等於頂點坐標的y值。當時觀察右圖。當時，則圖像開口於，一樣，則此時y 有最小值，且y只有最小值（聯繫圖像和二次函數即可得出結論）此時y值等於頂點坐標的y值。

一般地，如果兩個變數x、y之間的關係可以表示成 (k為常數，)的形式，那麼稱y是x的反比例函數。因為是一個分式，所以自變數X的取值範圍是。而有時也被寫成或。

這反比例函數的最值，實際上，和二次函數、一次函數與a的關係一樣，與k的取值範圍有關係，然而，它並不像二次函數那樣，最值是確定的，而是像一次函數那樣，只有當x有取值範圍后，最值才能有。

當時，且時， y隨著x的增大而增大。而當時，且時， y隨著x的增大而增大。這個是很容易弄混的，應當在草稿本上例題驗算一下。

當時，且時， y隨著x的增大而減小。而當時，且時， y隨著x的增大而減小。這個同樣是很容易弄混的，應當在草稿本上例題驗算一下，然後與上面的進行對比