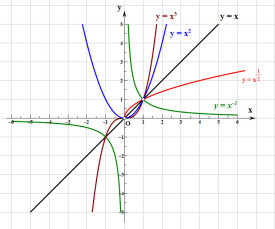
函數圖像
數學中的術語
在數學中,函數 f 的圖形(或圖象)指的是所有有序對(x, f(x))組成的集合。具體而言,如果x為實數,則函數圖形在平面直角坐標系上呈現為一條曲線。如果函數自變數x為兩個實數組成的有序對(x1, x2),則圖形就是所有三重序(x1, x2, f(x1, x2))組成的集合,呈現為曲面(參見三維計算機圖形)。
Functions images(函數的圖象)
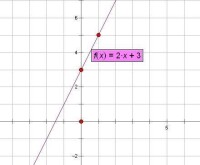
一次函數圖像
自變數x和因變數y有如下關係:
(k,b為常數,)
則稱y是x的一次函數。
特別地,當時,y是x的正比例函數。
若兩個變數x,y間的關係式可以表示為(k,b為常數,)的形式,則稱y是x的一次函數(x為自變數,y為因變數)。特別地,當時,稱y是x的正比例函數。
1. 作法與圖形:通過如下3個步驟(1)算出該函數圖象與Y軸和X軸的交點的坐標(2)描點;(3)連線,可以作出一次函數的圖象——一條直線。
2. 性質:在一次函數上的任意一點,都滿足等式:。
3. k,b與函數圖象所在象限。
當時,直線必通過一、三象限,從左往右,y隨x的增大而增大;
當時,直線必通過二、四象限,從左往右,y隨x的增大而減小;
當時,直線必通過一、二象限;當時,直線必通過三、四象限。
特別地,當時,直線通過原點表示的是正比例函數的圖象。
這時,當時,直線只通過一、三象限;當時,直線只通過二、四 象限。
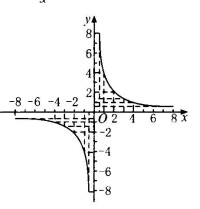
反比例函數圖像
已知點,請確定過點A、B的一次函數的表達式。 (1)設一次函數的表達式(也叫解析式)為。如果,則函數解析式為所以說正比例函數是特殊的一次函數。 (2)因為在一次函數上的任意一點,都滿足等式。所以可以列出2個方程: ① 和②。 (3)解這個二元一次方程,得到k,b的值。 (4)最後得到一次函數的表達式。 (5)在中,使x,y分別等於0,可求出兩個坐標系必定經過的兩點和。
1.當時間t一定,距離S是速度v的一次函數。。
2.當水池抽水速度f一定,水池中水量g是抽水時間t的一次函數。設水池中原有水量S。
形如 (k為常數且) 的函數,叫做反比例函數。
自變數x的取值範圍是不等於0的一切實數。
反比例函數的圖象為雙曲線。
如圖,上面給出了x分別為正和負(2和-2), 時的函數圖象。

雙鉤函數圖像
當時,由基本不等式可得:
當且僅當,即時取等號。
故其頂點坐標為,圖象在上是單調遞減的,在上是單調遞增
同理:當時,由基本不等式可得:
當且僅當,即時取等號。
故其頂點坐標為,
圖象在上是單調遞增,
在上是單調遞減的。
當 時可轉化為的情況
通常,作圖時,x看做0。代入得y,也就是縱軸坐標
有時,通過平移,把形如也看成反比例函數。
特殊位置關係
當平面直角坐標系中兩直線垂直時,其函數解析式中K值互為負倒數(即兩個K值的乘積為-1)
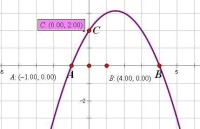
二次函數圖像
(a,b,c為常數,,且a決定函數的開口方向,時,開口方向向上,時,開口方向向下,IaI還可以決定開口大小,越大開口就越小,越小開口就越大.)
則稱y為x的二次函數。
二次函數表達式的右邊通常為二次三項式。
表達式
一般式:(a,b,c為常數,)
頂點式: [拋物線的頂點]
交點式:[僅限於與x軸有交點和 的拋物線]
註:在3種形式的互相轉化中,有如下關係:
圖象
在平面直角坐標系中作出二次函數的圖象,
可以看出,二次函數的圖象是一條拋物線。
性質
1.拋物線是軸對稱圖形。對稱軸為直線。
對稱軸與拋物線唯一的交點為拋物線的頂點P。
特別地,當時,拋物線的對稱軸是y軸(即直線)
2.拋物線有一個頂點P,坐標為
當時,P在y軸上;當時,P在x軸上。
3.二次項係數a決定拋物線的開口方向和大小。
當時,拋物線向上開口;當時,拋物線向下開口。
越大,則拋物線的開口越小。
4.一次項係數b和二次項係數a共同決定對稱軸的位置。
當a與b同號時(即),對稱軸在y軸左;
當a與b異號時(即),對稱軸在y軸右。
5.常數項c決定拋物線與y軸交點。
拋物線與y軸交於
6.拋物線與x軸交點個數
時,拋物線與x軸有2個交點。
時,拋物線與x軸有1個交點。
時,拋物線與x軸沒有交點。X的取值是虛數( 的值的相反數,乘上虛數i,整個式子除以2a)
位置關係
二次函數各式中,)的圖象形狀相同,只是位置不同,它們的頂點坐標及對稱軸如下表:
解析式 頂點坐標 對 稱 軸
當時,的圖象可由拋物線向右平行移動h個單位得到,
當時,則向左平行移動個單位得到.
當時,將拋物線向右平行移動h個單位,再向上移動k個單位,就可以得到的圖象;
當時,將拋物線向右平行移動h個單位,再向下移動個單位可得到的圖象;
當時,將拋物線向左平行移動個單位,再向上移動k個單位可得到的圖象;
當時,將拋物線向左平行移動個單位,再向下移動個單位可得到的圖象;
因此,研究拋物線 的圖象,通過配方,將一般式化為的形式,可確定其頂點坐標、對稱軸,拋物線的大體位置就很清楚了.這給畫圖象提供了方便.
2.拋物線的圖象:當時,開口向上,當時開口向下,對稱軸是直線,頂點坐標是.
3.拋物線若,當時,y隨x的增大而減小;當時,y隨x的增大而增大.若,當時,y隨x的增大而增大;當時,y隨x的增大而減小.
4.拋物線的圖象與坐標軸的交點:
(1)圖象與y軸一定相交,交點坐標為;
(2)當,圖象與x軸交於兩點和,其中的是一元二次方程
的兩根.這兩點間的距離
當.圖象與x軸只有一個交點;
當.圖象與x軸沒有交點.當時,圖象落在x軸的上方,x為任何實數時,都有;當時,圖象落在x軸的下方,x為任何實數時,都有.
5.拋物線的最值:如果,則當時,y最小(大)值.
頂點的橫坐標,是取得最值時的自變數值,頂點的縱坐標,是最值的取值.