本構模型

用於表示某一種材料的本構關係的物理模型。因通常由彈簧、黏壺和滑塊等實體元件組成而得名。按性質可分為彈性模型、剛塑性模型、彈塑性模型、黏彈性模型、黏塑性模型和彈黏塑性模型。與之相應的性質常由模型參數表示。在岩土力學中應用較為廣泛。

土的應力-應變關係為彈性關係以及建立在彈性理論基礎上的本構模型。主要有文克爾地基模型，雙參數地基模型，彈性半空間地基模型，層向各向同性體模型，以及各種非線性彈性模型。

通過應變能函數的微分建立的本構模型。

式中，

式中W為應變能函數；為余能函數；和分別為應力張量和應變張量。

在特路斯代爾（Truesdell）1955年建議的簡單比率理論基礎上建立應力速率 和應變速率 之間關係為基礎的一類本構模型。其一般表達式為：

零級次彈性模型為增量胡克定律。

建立在彈塑性模型理論基礎上的一類本構模型。

已經建立的彈塑性模型很多，影響較大的有：劍橋模型；修正劍橋模型；拉特-鄧肯模型；邊界面模型；清華彈塑性模型、沈珠江三重屈服面模型等。

即應力張量與應變張量的關係。一般地，指將描述連續介質變形的參量與描述內力的參量聯繫起來的一組關係式。具體地講，指將變形的應變張量與應力張量聯繫起來的一組關係式，又稱本構方程。對於不同的物質，在不同的變形條件下有不同的本構關係，也稱為不同的本構模型。如線性彈性體本構模型的本構關係為胡克定律。彈塑性體、粘彈性體、熱彈性體等都有各自的本構關係。剛體也可以被看作一種簡單的本構模型。

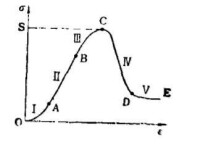
土的本構關係，亦稱“岩石的應力-應變關係”。岩石、岩體的應變或應變率與應力、溫度、時間及其他因素的函數關係。在固體力學中，表徵物體或結構變形與受力的關係。可分為線性（彈性體）本構關係與非線性（非彈性體）本構關係兩類。前者在簡單情況下即為應力-應變關係，應力分量與應變分量之間存在著一一對應的函數關係；而後者則複雜得多，一般天然岩石的本構關係均屬於此類，如圖1。通常，岩石的本構關係曲線亦稱為岩石應力-應變曲線。曲線大致可分為五個階段，C點表示岩石強度或破壞應力，OABC是破壞前區域，CDE是破壞後區域。本構關係是岩石力學中最重要的關係式，可用以確定一定應力場或環境條件下岩石的實際狀況。對於探索地球岩石圈的應力狀態以及地震成因理論等都有重要意義。

天然岩石的典型本構關係曲線

OA（Ⅰ）：作功硬化階段

AB（Ⅱ）：線彈性階段

BC（Ⅲ）：膨脹軟化階段

CD（Ⅳ）：可控破裂階段

DE（Ⅴ）：摩擦滑動階段

本構方程是由物質性質決定的，它不隨觀測者的改變而變化，因而作為相對運動的兩個觀測者在做材料試驗時應當得到相同的本構關係。即在做相對運動的坐標系中，本構方程應具有相同的形式。

同時，本構方程不因坐標系的選擇不同而不同，在各坐標系中均具有相同的形式，本構方程應當具有張量的性質。物質客觀性原理也成為坐標系無差異原理。

確定性原理認為物體中某點的狀態恆可由物體內各點的以往運動史唯一確定，而和未來的運動無關。

物體內諸點的運動對某點X的應力或其他物理量的影響，隨著離該點距離的增大而減小，特別是對大多數物質，只有X點鄰近質點的運動才對X點的應力有影響，而離開X點有限距離的物質點的運動對該點的應力沒有影響。換句話說，同一物體的兩個不同的運動歷史，只要保證兩個運動歷史在X點鄰域內是相同的，則X點的應力或其他物理量也是相同的。

物質客觀性原理、確定性原理和局部作用原理也稱為Noll三原則，由此可以導出簡單物質的本構關係。

自然界中的物質一般都存在對稱性，本構方程必須能夠反映這種對稱性。線性彈性力學的理論已證明，理論上應力一應變間存在81個彈性常數。由於應力和應變張量均為對稱張量，獨立的彈性常數下降到21個，正交各向異性物質具有三個相互正交的對稱面，可以導出獨立的彈性常數為9個。橫觀各向同性材料有5個獨立的彈性常數，而各向同性材料則只有2個獨立的彈性常數。

離現時刻越遠的過去的歷史對現時刻應力和其他狀態物理量的影響越小。蠕變材料等的本構方程都必須滿足這一原理。

物質的本構關係必須滿足一些普遍原理，如質量守恆原理、動量守恆原理、動量矩方程、局部能量守恆原理、熵產率原理等。

本構方程中各項的量綱必須一致，同時要特別注意一些特殊函數（如對數函數、指數函數等）的自變數量綱。從事本構關係研究時，對量綱一致性原理必須有足夠的重視，否則，即使提出的本構關係能很好地擬合試驗數據，但在實際應用中可能會得到完全錯誤的結果。

文克爾地基模型是由捷克工程師E·文克爾（E·WINKLER）1876年提出的。基本內容為：地基上任一點所受的壓力強度p與該點的地基沉降S成正比，即式中k-基床係數，表示產生單位沉降所需的反力，單位。

在文克爾地基模型下，地基上某點的沉降之與該點土作用的壓力有關，與其他點的壓力無關。力學性質與水相近的地基，例如抗剪強度很低的半液態土﹙如淤泥、軟粘土﹚地基或基底下塑性區相對較大時，採用文克爾地基模型就相對比較合適。文克爾地基又可稱為稠密液體地基，基床係數K相當於液體的密度，地基反力相當於液體的浮力。此外，厚度不超過梁或板的短邊寬度之半的薄壓縮層地基也適於採用文克爾地基模型。這是因為在面積相對較大的基底壓力作用下，薄層中的剪應力不大的緣故（實際上，沉陷也發生在受壓範圍以外）。

文克爾地基模型忽略了地基中的剪應力，這與實際情況是不相符的。正是由於剪應力的存在，地基中的附加應力才能向旁擴散分佈，使基底以外的地表發生沉降。文克爾模型中把基礎當作絕對剛性的，忽視上部結構的存在，把基礎看成地基上孤立的梁和板，而事實上結構-基礎-地基是相互作用的。

1958-1963年間，英國劍橋大學的Roscoe等根據正常固結粘土和弱超固結粘土的三軸試驗，提出的劍橋粘土的本構模型，標誌著人們在土體力學特性認識上的第一次飛躍。他們將“帽子”屈服準則、正交流動準則和加工硬化規律系統地應用於Cam模型之中，並提出了臨界狀態線、狀態邊界面、彈性牆等一系列物理概念，構成了第一個比較完整的土塑性模型。Roscoc和Burland又進一步修正了劍橋模型，認為劍橋模型的屈服面軌跡應為橢圓，給出了眾所周知的修正劍橋模型。可以這樣說，劍橋模型開創了土力學的臨界狀態理論。

試驗證明，對於正常固結粘土和弱固結的飽和重塑粘土，孔隙比e與外力p，q之間存在有唯一的關係，且不隨應力路徑而發生變化。該模型試圖描述室內試驗所觀察到的現象，即從某一初始狀態開始載入直到最終維持塑性常體積變形的臨界狀態，其基本組成如下：

（1）在平面中，存在一條曲線，在正常固結粘性土中的所有應力遵循此路徑，這被稱為正常固結線（NCL）。這條線提供了體積硬化規則，可以被廣義化為一般應力條件。

（2）在空間中存在一條線，所有的殘餘狀態都遵循此路徑，而與實驗類別和初始條件無關。這條線與平面中的正常固結線平行，在此線上，剪切變形發生而沒有體積變形發生。

（3）從固結排水和不排水實驗中所得到的應力路徑位於唯一的狀態面，通稱為Roscoe面。事實上，在不排水路徑中，土隨著塑性體積應變的發展而硬化。其中，體積應變的彈性和塑性應變增量之和保持常數。Roscoe麵價值在於給出了屈服面類型的一個選擇依據。