球坐標
用於地理學、天文學等的坐標系
右圖顯示了球坐標的幾何意義:原點與點P之間的徑向距離r,原點到點P的連線與正z-軸之間的天頂角θ,以及原點到點P的連線,在xy-平面的投影線,與正x-軸之間的方位角φ。
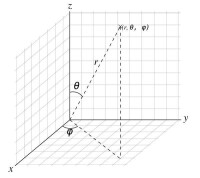
圖1.
在學術界內,關於球坐標系的標記有好幾個不同的約定。按照國際標準化組織建立的約定(ISO31-11),徑向距離、天頂角、方位角,分別標記為。這種標記在世界各地有許多使用者。通常,物理界的學者也採用這種標記。而在數學界,天頂角與方位角的標記正好相反:φ被用來代表天頂角,θ被用來代表方位角。數學界的球坐標標記是。這種標記的優點是較廣的相容性;在二維極坐標系與三維圓柱坐標系里,ρ都同樣地代表徑向距離,θ也都同樣地代表方位角。本條目採用的是物理標記約定。
假設P點在三維空間的位置的三個坐標是。那麼,是從原點到P點的距離,是從原點到P點的連線與正z-軸的夾角,是從原點到P點的連線在xy-平面的投影線,與正x-軸的夾角。
這裡,θ代表天頂角,φ代表方位角。當時,θ與φ都一起失去意義。當或時,φ失去意義。
如想要用球坐標,找出點P在空間的地點,可按照以下步驟:
1.從原點往正z-軸移動r單位,
2.用右手定則,大拇指往y-軸指,x-軸與z-軸朝其他手指的指向旋轉θ角值,
3.用右手定則,大拇指往z-軸指,x-軸與y-軸朝其他手指的指向旋轉φ角值。
地理坐標系用兩個角值,緯度與經度,來表示地球表面的地點。正如二維直角坐標系專精在平面上,二維球坐標系可以很簡易的設定圓球表面上的點的位置。在這裡,我們認定這圓球是個單位圓球;其半徑是1。通常我們可以忽略這圓球的半徑。在解析旋轉矩陣問題上,這方法是非常有用的。
球坐標系適用於分析一個對稱於點的系統。舉例而言,一個圓球,其直角坐標方程式為,可以簡易的用球坐標系來表示。
當求解三重積分時,如果定義域為圓球,則面積元素是
體積元素是
用來描述與分析擁有球狀對稱性質的物理問題,最自然的坐標系,莫非是球坐標系。例如,一個具有質量或電荷的圓球形位勢場。兩種重要的偏微分方程式,拉普拉斯方程與亥姆霍茲方程,在球坐標里,都可以成功的使用分離變數法求得解答。這種方程式在角部分的解答,皆呈球諧函數的形式。
球坐標的概念,延伸至高維空間,則稱為超球坐標(n-sphere)。
