有限域
僅含有限多個元素的域
目錄
最簡單的有限域是整數環Z 模一個素數p得到的商環Z/(p),由p個元素0,1,…,p-1組成，按模p相加和相乘。這p個元素的域簡記為Fp，有如下性質：pα=0;，αp=α其中α、b∈Fp。Fp稱為特徵為p的素域，它與素數成一一對應。
任一有限域的特徵是一素數。一個特徵為素數 p的有限域F仍滿足上述的第一、第二兩條性質，F包含一個最小的子域，由單位元素e的一切倍數0,e,2e…,(p-1)e組成，它與Z/(p)同構。因此一個特徵為p的有限域總是以特徵為p的素域Fp作為子域。
特徵p的有限域F也是Fp上一個有限維線性空間。設維數為n，F對Fp的一基為ε1,ε2,…,εn,則F由下列pn個元素組成：所以｜F｜=pn。F的乘法群F*=F-{0}是一個pn-1階循環群，恰好是多項式的全部根。因此,F恰好由在Fp的代數閉包內的全部根組成。反之，任給一個素數p和一個正整數n，恆存在一個含pn個元素的有限域，它就是多項式在Fp上的分裂域。元素個數相同的任何兩個有限域是同構的。因此，在同構意義下，對每個素數p和一個正整數n，存在一個而且只有一個含pn個元素的有限域，這個有限域記作GF(pn)。
順便指出，J.H.M.韋德伯恩於1905年證明了“有限除環必是乘法交換的”。因此，有限除環就是現在所說的有限域。
對n的每個因子d,GF(pn)有一個而且只有一個含pd個元素的子域。因此,GF(pn)的子域和n的因子成一一對應。
有限域F=GF(pn)有一個弗羅貝尼烏斯自同構,有,對所有x∈F，當且僅當n|k,因而σ生成一個n階循環群G，|G|=【F:Fp】。F/Fp是一個伽羅瓦擴張，G是它的群，對n的每個因子d,在伽羅瓦對應下，子群〈〉和它的不動域GF(
)成一一對應。
有限域
對於α∈F=GF(pn),規定：
,
稱為α從F到Fp的跡，在不致引起混淆的情況下，簡記作Tr。Tr(x)是線性空間F/Fp上的一個線性函數，是加法群F到加法群Fp的一個滿同態。
對α∈F，規定：
有限域
稱為α從F到Fp的范數，可簡記作N(α)。N是乘法群F*到F壩的一個滿同態。
設ƒ(x)是元素α∈F＝GF(pn)在Fp上的極小多項式，ƒ(x)的次數稱為α的次數,α的次數d等於【Fp(α):Fp】,因而d│n。假設α≠0,則α的次數d和α在乘法群F*中的階e有如下的關係:d是最小正整數，使得pd呏1(тode), 即α的次數等於pтode的指數。
若α(≠0)的階等於pn-1,則α稱為F的一個本原元素。它的極小多項式ƒ(x)稱為（n次）本原多項式。
設g(x)是Fp【x】中一個不可約多項式, 且g(x)≠x,若存在一個最小正整數r使得 xr呏1(modg(x))，則r稱為g(x)的周期。一個非零的 α∈F的極小多項式ƒ(x)的周期，等於α的階。特別，一個n次本原多項式的周期等於pn-1。設一個不可約多項式g(x)(≠x)的周期為r,則g(x)k的周期等於rps，其中ps-1
Fp【x】的一個m 次不可約多項式g(x)在GF(pn)內有根；；這三者是等價的。因此,Fp【x】中n次不可約多項式全是的因式,n次不可約多項式的個數為,其中μ(d)是麥比烏斯函數。用表示Fp上全部n次不可約多項式(首項係數為1)的積，於是。n次本原多項式的個數為，其中φ(m)為歐拉函數。
Fp上一個多項式ƒ(x)（次數n≥1）的分解對現代通信有很重要的關係。在理論上它和商環R=Fp【x】/(ƒ(x))的代數結構又密切相關。令，則V有如下的性質。
① Fp嶅V嶅R，V為R的一個子環而且半單，因而V是一些與Fp同構的子域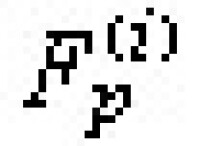
的直和,i=1,2,…,g;g等於V作為Fp上線性空間的維數，g也是ƒ(x)在Fp上相異的不可約因式的個數。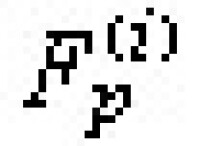的單位元素ei(i=1,2,…,g),構成R的互相正交的本原冪等元而且。
有限域
有限域
② 令，則 Pi(x)為一個不可約多項式的方冪,,而且·。pj(x)稱為ƒ(x)的准素因式。
為了給出分解ƒ(x)的實際的計演演算法，還有如下性質。
③ R有一個F自同構π：π(g(x))=g(x)p，g(x)∈R，則V就是屬於π的特徵值1的全部特徵向量和0構成的特徵子空間。於是有:a.設η∈V,g(x)為ƒ(x)的一個因式，如果g(x)凲η-i,i=0,1,…,p-1,則為一個非平凡的分解，而且這個條件也是必要的。上面的乘積中出現的因式兩兩互素。b.設η1,η2,…,ηg為V對Fp的一基，則g(x)為一個不可約多項式的方冪，其充分必要條件是每個ηi與Fp中一個元素modg(x)同餘。
分解ƒ(x)的步驟大致如下：不妨設η1=1。用η2按a.分解ƒ(x),得到的因式記為ƒ1(x),ƒ2(x),…,ƒr(x),r≤g-1，每個ƒi(x)按b.進行檢驗，如果ƒi(x)含有兩個或兩個以上不同素因式，則存在一個ηj,j>2，使得ƒi(x)和ηj滿足a.中的條件，用ηj對ƒi(x)進行分解, 如此進行下去，經有限步后，即得到ƒ(x)的全部准素因式pi(x)，i=1,2,…,g,而pi(x)的分解是容易的。至於V的求得，則是屬於線性方程組的問題。
判定一個n次多項式ƒ(x)是否是本原的，還沒有一般的方法，只有用試算的辦法去計算具體的ƒ(x)的周期之後才能作出判斷。F2上 168次以下的三項或五項的本原多項式（每個次數給出一個）已經有表可查。計算出全部F上n次不可約多項式大致有兩種途徑，一是直接分解第2n-1個分圓多項式，一是篩法，它正如求有理素數的篩法一樣。F2上16次以下的全部不可約多項式和17～34次具有各種周期的不可約多項式有表可查。
令R表示由有限域 F上的形式冪級數組成的環。ƒ可逆的充分必要條件是α0≠0。如果存在一個正整數l使得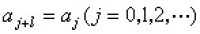
,那麼ƒ就稱為循環的。若ƒ是循環的，則最小的l就稱為ƒ的周期。全部循環冪級數構成R的一個子環，記作C。R中所有形如h(x)/g(x)的真分式構成R的一個子環，記作B,這裡h(x)和g(x)是F【x】中的多項式, h(x)的次數小於g(x)的次數，且g(0)≠0。可以證明,C=B。因此,B與C的關係正如正的真分數（分母與10互素）與循環小數的關係一樣。有限域在現代通信（例如編碼）、組合數學（例如有限幾何、區組設計、差集合、正交拉丁方）以及正交試驗設計等各方面，有廣泛的應用。
有限域
僅以線性反饋移位寄存器序列（以下簡稱線性移存器序列）為例，敘述如下。有限域F上一個非退化n位線性移存器序列，從一個非零初態x0，x1,…，xn-1出發產生一個輸出序列, 稱之為一個n位線性移存器序列，它在 t時刻的輸出xt是它前 n個時刻的輸出的線性函數，式中b)j∈F，是與時刻 t無關的常數。這個n位非退化線性移存器的功能由上述遞推關係所刻畫。將輸出序列表成冪級數,此時x相當於移存器中的遲延運算元。令,則α(x)·g(x)為一個次數不大於(n-1)的多項式，記為h(x)，於是α(x)=h(x)/g(x)，因而α(x)是一個循環級數，α(x)的周期等於g(x)/d(x)的周期，其中d(x)=(g(x),h(X))。若g(x)是可約的，則α(x) 的周期還依賴於所給的初態。若 g(x)是不可約的，從任一非零初態出發得到的α(x)有同一周期，即g(x)的周期。反之，任給一個n次多項式g(x)，且g(0)=1,則可以造出一個非退化 n位線性反饋移存器序列使得它的功能由g(x)所確定。
應用n次本原多項式可以造出周期最長的n位線性反饋移存器序列。
參考書目
L.Dickson,Linear Algebraic Groups, with an Exposition of the Galois Field Theory, Dover,NewYork, 1958.
A.Albert,Fundamental Concepts of Higher Algebra, Univ. of Chicago Press, Chicago, 1956.
目錄