lu分解

lu分解

在線性代數中，LU分解(LU Decomposition)是矩陣分解的一種，可以將一個矩陣分解為一個單位下三角矩陣和一個上三角矩陣的乘積（有時是它們和一個置換矩陣的乘積）。LU分解主要應用在數值分析中，用來解線性方程、求反矩陣或計算行列式。

目錄

1簡介 2演算法 3示常式序

簡介

lu分解

lu分解

將係數矩陣A轉變成等價兩個矩陣L和U的乘積，其中L和U分別是單位下三角矩陣和上三角矩陣。當A的所有順序主子式都不為0時，矩陣A可以分解為A=LU（所有順序主子式不為0，矩陣不一定不可以進行LU分解）。其中L是下三角矩陣，U是上三角矩陣。

演演算法

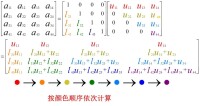
LU分解在本質上是高斯消元法的一種表達形式。實質上是將A通過初等行變換變成一個上三角矩陣，其變換矩陣就是一個單位下三角矩陣。這正是所謂的杜爾里特演演算法（Doolittle algorithm）：從下至上地對矩陣A做初等行變換，將對角線左下方的元素變成零，然後再證明這些行變換的效果等同於左乘一系列單位下三角矩陣，這一系列單位下三角矩陣的乘積的逆就是L矩陣，它也是一個單位下三角矩陣。這類演演算法的複雜度一般在(三分之二的n三次方) 左右。

示常式序

import java.util.Arrays;

public class DoolittleDecomposition {

private double[][] data;

private double[][] l;

private double[][] u;

private int n;

public DoolittleDecomposition(double[][] data) {

if (data == null || data.length == 0 || data.length != data[0].length) {

throw new RuntimeException("不是一個方陣");

}

this.data = data;

n = data.length;

l = new double[n][n];

u = new double[n][n];

countLU();

}

protected void countLU() {

for (int i = 0; i < n; i++) {// 第一步，計算L的第一列和U的第一行：U1i=A1i,Li1=Ai1/U11

u[0][i] = data[0][i];

l[i][0] = data[i][0] / u[0][0];

}

//計算U的第r行，L的第r列元素

//uri=ari-Σ(k=1->r-1)lrkuki (i=r,r+1,...,n)

//lir=air-Σ(k=1->r-1)likukr (i=r+1,r+2,...,n且r≠n)

for (int r = 1; r < n; r++) {

for (int i = r; i < n; i++) {

u[r][i] = data[r][i] - sumLrkUki(r, i);

if(i==r) l[r][r]=1;

else if(r==n) l[n][n]=1;

else l[i][r] = (data[i][r] - sumLikUkr(r, i)) / u[r][r];

}

}

}

private double sumLrkUki(int r, int i) {

double re = 0.0;

for (int k = 0; k < r; k++) {

re += l[r][k] * u[k][i];

}

return re;

}

private double sumLikUkr(int r, int i) {

double re = 0.0;

for (int k = 0; k < r; k++) {

re += l[i][k] * u[k][r];

}

return re;

}

public double[][] getData() {

return data;

}

public double[][] getL() {

return l;

}

public double[][] getU() {

return u;

}

public static void main(String[] args) {

double[][] data= {

{1,2,6},

{2,5,15},

{6,15,46},

};

DoolittleDecomposition dd = new DoolittleDecomposition(data);

double[][] l = dd.getL();

double[][] u = dd.getU();

int n = l.length;

System.out.println("L陣：");

for (int i = 0; i < n; i++) {

System.out.println(Arrays.toString(u[i]));

}

System.out.println("---------------------");

System.out.println("U陣：");

for (int i = 0; i < n; i++) {

System.out.println(Arrays.toString(l[i]));

}

}

}

Matlab

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

%LU分解法求解Ax=b，假定A矩陣可進行LU分解以及對角線元素均不為0

function [x] = Dool(A,b)

n=length(A);A(2:n,1)=A(2:n,1)/A(1,1);

for t=2:n-1 %進行LU分解

A(t,t:n)=A(t,t:n)-A(t,1:t-1)*A(1:t-1,t:n);

A(t+1:n,t)=(A(t+1:n,t)-A(t+1:n,1:t-1)*A(1:t-1,t))/A(t,t);

end

A(n,n)=A(n,n)-A(n,1:n-1)*A(1:n-1,n);

L=tril(A,-1)+eye(n);U=triu(A); %矩陣A分解出L和U

for t=2:n %解Lx=b

b(t)=b(t)-L(t,1:t-1)*b(1:t-1);

end

b(n)=b(n)/U(n,n); %解Ux=b

for t=1:n-1;

k=n-t;b(k)=(b(k)-U(k,k+1:n)*b(k+1:n))/U(k,k);

end

x=b; %方程Ax=b的解即為x

改進

（i）Doolittle分解

對於非奇異矩陣（任n階順序主子式不全為0）的方陣A，都可以進行Doolittle分解，得到，其中L為單位下三角矩陣，U為上三角矩陣；這裡的Doolittle分解實際就是Gauss變換；

（ii）Crout分解

對於非奇異矩陣（任n階順序主子式不全為0）的方陣A，都可以進行Crout分解，得到，其中L為下三角矩陣，U為單位上三角矩陣；

（iii）列主元三角分解

對於非奇異矩陣的方陣A，採用列主元三角分解，得到，其中P為一個置換矩陣，L，U與Doolittle分解的規定相同；

（iv）全主元三角分解

對於非奇異矩陣的方陣A，採用全主元三角分解，得到，其中P，Q為置換矩陣，L，U與Doolittle分解的規定相同；

（v）直接三角分解

對於非奇異矩陣的方陣A，利用直接三角分解推導得到的公式（Doolittle分解公式或者Crout分解公式），可以進行遞歸操作，以便於計算機編程實現；

（vi）“追趕法”

追趕法是針對帶狀矩陣（尤其是三對角矩陣）這一大稀疏矩陣的特殊結構，得出的一種保帶性分解的公式推導，實質結果也是LU分解；因為大稀疏矩陣在工程領域應用較多，所以這部分內容需要特別掌握。

（vii）Cholesky分解法（平方根法）和改進的平方根法

Cholesky分解法是是針對正定矩陣的分解，其結果是。如何得到L1，實際也是給出了遞歸公式。

改進的平方根法是Cholesky分解的一種改進。為避免公式中開平方，得到的結果是，同樣給出了求T,L的公式。

小結：

（1）從（i）~（iv）是用手工計算的基礎方法，（v）~（vi）是用計算機輔助計算的演演算法公式指導；

（2）這些方法產生的目的是為了得到線性方程組的解，本質是高斯Gauss消元法。

目錄