屈服函數
屈服函數
在一定的變形條件(變形溫度、變形速度等)下,只有當各應力分量之間符合一定關係時,質點才開始進入塑性狀態,這是描述受力物體進入塑性狀態並使塑性變形繼續進行所必須遵守的力學條件,這種力學條件一般可表示為一個時間的函數,此函數稱為屈服函數。
屈服:物體受到荷載作用后,隨著荷載增大,由彈性狀態到塑性狀態的這種過渡,叫做屈服。
一般情況下,屈服條件與應力、應變、時間、溫度等有關,而且是它們的函數,這個函數稱為屈服函數。
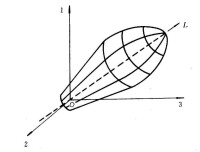
在應力空間內屈服函數表示為屈服面。
根據不同的應力路徑實驗,在應力空間將這些屈服點連接起來,就形成一個區分彈性和塑性的屈服面。
屈服面在π平面上的跡線一般稱為π平面上的屈服曲線;而屈服面與子午平面的交線稱為子午平面上的屈服曲線。
屈服函數
(1) 要有一個判別材料是否處於彈性階段還是塑性階段的判斷式, 即屈服條件: 初始屈服條件和後繼屈服條件。
(2) 應力應變是非線性關係。
(3) 應力應變之間不存在單值關係。
初始屈服條件:對於單向拉伸時拉伸應力等於材料的屈服應力時開始屈服, 但是在一般情況下一點的應力狀態時六個應力分量, 我們不能簡單地說哪一個分量達到屈服應力,這一點開始屈服. 但有一點可以肯定, 屈服條件應該和這六個分量有關, 把它寫成函數關係,該函數就稱為初始屈服條件。
我們已經知道, 靜水應力不引起塑性變形, 那麼屈服條件只和應力偏量有關, 屈服條件可以寫為函數形式。