賦范代數

設A是賦范線性空間，如果在A上定義了乘法，即對於A中任何兩個元素x，y，對應有A中的一個元，稱為x與y的乘積，並記為xy。而且乘法具有下列性質：①(xy)z=x(yz)，② α(xy)＝(αx)y＝x(αy)，③(x+y)z＝xz+yz，z(x+y)＝zx+zy，④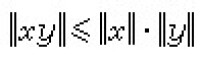，則稱A 是賦范代數。又當A是巴拿赫空間時,A就稱為巴拿赫代數。如果對A中任何兩個元x，y都成立xy=yx,就稱A是交換的。A中元e如果使ex=xe=x對任何x∈A成立，e就稱為A的單位元。當A有單位元時，單位元必是惟一的。在有單位元e的賦范代數A中，對元x，如果有y使xy=yx=e,就稱y是x的逆元。

在分析學中遇到的許多重要的巴拿赫空間在適當地規定乘法后就成為巴拿赫代數。典型的例子是：實數R上復值勒貝格可積函數全體l1(R)在l1范數下成為巴拿赫空間，如果以卷積

作為l1(R)上乘法，那麼它成為交換的巴拿赫代數。

巴拿赫代數的概念雖然相當簡單，但在調和分析、運算元理論、函數代數等許多數學領域中有廣泛的應用。由於在巴拿赫代數中除線性運算外還有乘法運算，就能更多地利用代數的方法。實質上，在巴拿赫代數中，代數運算（加法、數乘、乘法）與范數之間有著深刻的內在聯繫，顯示代數方法對分析問題（與極限有關的問題）的研究起著更大的作用。

1939年,И.М.蓋爾范德奠定了巴拿赫代數的理論基礎。交換巴拿赫代數理論一出現，就在它的初次應用(對三角級數理論中維納定理的簡潔證明) 中顯示出巨大威力，迅速吸引了大批數學家的注意。從此，巴拿赫代數理論的研究就蓬勃開展起來。今天，這個理論不僅是分析學中的重要工具，而且它本身也是近代數學研究的一個重要領域。近年來，它在場論中的應用也是令人注目的，它的理論本身綜合著函數理論，抽象代數等的技巧，有著豐富的成果。

元素的譜 設A是復的有單位元e的巴拿赫代數,x∈A,如果複數λ使λe-x有逆元，就稱λ為x的正則點,否則就稱λ為x的譜點。x的譜點全體稱為x的譜，記為σ(x)。關於元素的譜, 蓋爾范德得到的主要結論是：任何元x的譜σ(x)是複數域C的非空有界閉集，而且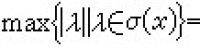，數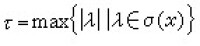稱為x的譜半徑。

交換巴拿赫代數 在有單位元E的復巴拿赫代數A中對任何元素x∈A，必有λ∈σ(x)，這時λe-x是設有逆元的。因此，如果A中任何非零元都有逆元，那麼A中任何元x都是e的倍數，即A是個一維空間（蓋爾范德-梅休爾定理）。在巴拿赫代數A上的線性泛函ƒ，如果對任何兩個元x、y，ƒ(xy)=ƒ(x)ƒ(y)成立，稱ƒ是乘性線性泛函，這種泛函必定是連續的。非零的乘性線性泛函 ƒ的零空間M ƒ={x｜ƒ(x)=0}必是A的閉雙側理想(即M ƒ是A的線性子空間，且對x∈M ƒ,y∈A，xy和yx都在M ƒ中)，且A/M ƒ是一維空間，蓋爾范德把代數中的理想理論與蓋爾范德-梅休爾定理結合起來，證明了下面的結論：設A是交換的有單位元e的復巴拿赫代數，則ƒ凮M ƒ是A上非零乘性線性泛函全體Ω到A的極大理想全體上的雙射，而A中任何無逆元的x，必定有含有x的極大理想，從而必有ƒ∈Ω使ƒ(x)=0，因此對任何x∈A，

σ(x)=｛ƒ(x)｜ƒ∈Ω｝，

Ω是A*的子集，當A*用弱*拓撲時,Ω是緊集，於是Ω是個緊豪斯多夫空間,拓撲空間Ω稱為A的譜空間，對於x∈A，記x(ƒ)＝ƒ(x)(ƒ∈Ω),x(·)是Ω上連續函數，也記為憫，它稱為元x 的函數表示（或蓋爾范德變換）。xx(·)是A→C(Ω)(Ω上復值連續函數全體)中的代數同態。於是，A 就表示為C(Ω) 的一個子代數。｜x(·)｜的最大值就是x的譜半徑。特別，A是半單純的(即A的所有極大理想的交為｛0｝)，或A中譜半徑為0的元只有0,都是使這個表示是一對一的充分而且必要的條件。

作為應用，考慮絕對收斂的三角級數全體

，

W 中的線性運算及乘法就用函數的通常運算。然而對於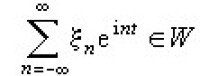，以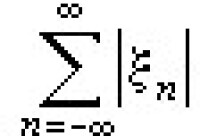作為這個元的范數。這樣，W 就成為一個交換的有單位元的復巴拿赫代數。恆等於1的函數是W 的單位元。任取t0∈【-π,π】,從W 到複數域C的映射xx(t0)是W上的非零乘性線性泛函，不難證明這是W上非零乘性線性泛函的一般形式，於是對 x ∈W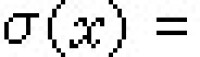，。這樣就很快得到著名的維納定理(它的原始證明是純函數論的方法)；如果 x(t)是絕對收斂的三角級數且 x(t)≠0(t∈【-π，π】)，則也是絕對收斂的三角級數。

函數代數 一類重要的、特殊的交換巴拿赫代數。它與解析函數論、多複變函數論、函數逼近論等有密切關係，是50年代迅速發展起來的一個分支。設Ω是緊豪斯多夫空間,C(Ω)、CR(Ω)分別是Ω上的復值、實值連續函數全體以最大模作為范數,C(Ω)、CR(Ω)都是交換的巴拿赫代數。設A是C(Ω)的閉子代數，如果A 含有常數函數，且分離Ω中點(即對Ω中不同的點ω1,ω2,必有ƒ∈A使得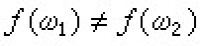）,稱A是Ω上函數代數。例如Ω是n維復空間Cn的緊集,P(Ω)、R(Ω)、A(Ω)分別是多項式、有理函數、Ω上連續且在Ω內部解析函數全體所生成的C(Ω)的閉子代數，這些都是很重要的函數代數。函數代數A如果使｛Reƒ|ƒ∈A｝生成的閉子代數是CR(Ω)，稱A是狄利克雷代數，它是又一種重要的函數代數。人們在一般巴拿赫代數觀念下，通過對這些具體代數的研究，不僅能把函數論中許多重要結果簡化證明或加以推廣，而且還能獲得新的結果，提出新的課題，從而促進了函數論的發展。

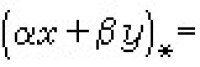
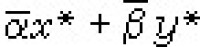對稱巴拿赫代數 如果在巴拿赫代數A中還有對合運算*:xx*,它具有下列性質:①(x*)*=x,②，③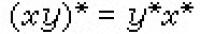，這時稱A為有對合的巴拿赫代數或巴拿赫*代數。如果對合還使得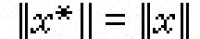，A就稱為對稱巴拿赫代數。研究這種代數的重要工具是正線性泛函（即對任何x∈A成立ƒ(x*x)≥0,的A上線性泛函ƒ）。從正泛函可以得到對稱巴拿赫代數的*表示。群代數是對稱巴拿赫代數的一個典型例子。設G 是局部緊的拓撲群,μ是G上的(左不變)哈爾測度,則G上關於μ可積的函數全體 l1(G,μ)是對稱巴拿赫代數。l1(G,μ)再加上單位元后的代數稱為G 的群代數。利用正泛函可以證明群代數的不可約*表示是完全的。當G是交換的局部緊群時,G的群代數是交換的對稱巴拿赫代數。通過傅里葉變換可以證明，群代數的譜空間Ω與G 的特徵群弿 同胚，並且l2(G)與l2(弿)同構。由此可以得到龐特里亞金對偶性定理的一個簡單的分析和證明。

C*代數 如果巴拿赫代數A有對合運算*，並且對合使得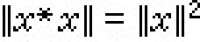，則稱A是C*代數。

緊豪斯多夫空間Ω上復值連續函數全體C(Ω),以取複數共軛作為對合時是有單位元的交換C*代數。復希爾伯特空間H上線性有界運算元全體B(H),以取運算元的共軛運算作為對合時是有單位元的C*代數，當h的維數≥2時，B(H)不是交換的。這些都是C*代數的典型例子。

如果A是有單位元的復交換C*代數，Ω是A的譜空間，則蓋爾范德變換xx(·)是A到C(Ω)上的完全同構，即xx(·)是保持對合及范數的代數同構。

態與GNS構造 C* 代數理論中最重要的部分。設A是有單位元e的復C*代數，在e上取值為1的A上正線性泛函ƒ稱為A上的態。當ƒ是A上的態時,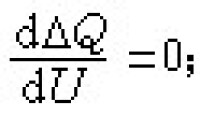是A的左理想。在A/gƒ上定義內積,完備化后得到的希爾伯特空間為hƒ。對於x∈A，令

,Πƒ(x)是A/gƒ上的有界線性運算元，它可惟一地開拓為hƒ上的有界線性運算元，仍記為Πƒ(x)。這時，A到B(Hƒ)的映射Πƒ:xΠƒ(x)不僅是線性的，而且保持乘法和對合。｛Πƒ,hƒ｝是A的*表示，或者說Πƒ是A在希爾伯特空間Hƒ上的*表示，而且Hƒ中有單位向量捳使

，

式中右邊是希爾伯特空間中的內積。以上就是著名的GNS構造。用它可以證明：對任何復C*代數A,必存在復希爾伯特空間h,使得A完全同構於B(h)的某個閉*子代數。上面兩個關於完全同構的定理都稱為蓋爾范德－奈伊瑪克定理。GNS構造有著重要的物理意義：如果C*代數相應於量子系統的觀察量代數，那麼C*代數的態就是量子系統的狀態，公式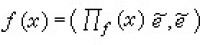是觀察量x在狀態ƒ中的期望值。這是通常量子理論中所熟知的。C*代數在抽象調和分析、量子物理等領域中也有重要的應用。

馮·諾伊曼代數 一類由希爾伯特空間上的有界線性運算元組成的代數。設h是復希爾伯特空間，在B(h)（h上有界線性運算元全體）中，除了運算元范數所導出的拓撲外，常用的有強（弱）運算元拓撲。記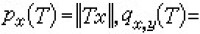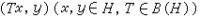，由{ px(·)}(x ∈h )({qx,y(·)}(x,y∈h))導出的B(h)的拓撲稱為B(h)的強(弱)運算元拓撲。B(h)中包含恆等運算元I的弱閉(即按弱運算元拓撲為閉的)*子代數稱為馮·諾伊曼代數。這個定義中的“弱閉”換成“強閉”是一樣的。

J.馮·諾伊曼為了把20世紀20年代由（A.）E.諾特與E.阿廷所發展的非交換環理論推廣到希爾伯特空間的情形。他引進了運算元環的概念。從此一個新的重要的數學領域誕生了，它先於巴拿赫代數的理論。後來為紀念這一數學理論的奠基者，將他的運算元環稱為馮·諾伊曼代數。

交換子和二次交換子定理 設M 嶅B(h),與M 中任何運算元可交換的運算元全體稱為M 的交換子，記為M 1。馮·諾伊曼的第一個結果是二次交換子定理：如果U是馮·諾伊曼代數，那麼U=U″。由此，對任何M 嶅B(h),包含M 的最小馮·諾伊曼代數等於（M ∪M *）"(這裡)。這個定理給予馮·諾伊曼代數一個代數的等價定義:B(h)中滿足U=U"的*子代數稱為馮·諾伊曼代數。這是馮·諾伊曼研究運算元環的主要工具之一。

因子分類 又稱維數理論。若U是馮·諾伊曼代數，U∩U′稱為U的中心，中心為｛αI｜α∈C｝的馮·諾伊曼代數稱為因子。30年代到40年代，馮·諾伊曼和F.J.默里合作，對馮·諾伊曼代數進行了深入的研究，提出了約化理論。指出馮·諾伊曼代數可以表達為因子的連續直接和（積分）。這樣，對馮·諾伊曼代數的研究可以歸結為對因子的研究。類似於經典的非交換代數理論，研究馮·諾伊曼代數U的主要工具是U中的冪等自共軛元，即希爾伯特空間上的正交投影。而問題的複雜性在於，因子中可以沒有極小的非零投影。馮·諾伊曼和默里指出，因子U中的兩個投影P1和P2還是可以比較“大小”的。如果U中有部分等距運算元V把P1h等距地變成P2h的閉子空間且V在(P1h)寑上為0，就稱P1比P2小。這種在U的投影全體中所引入的大小順序關係也可以用維數函數來描述。即對U中的每個投影給以一個非負實數或∞，它可以刻畫投影的大小，在可能相差一個常數倍的意義下，維數函數是惟一的。維數函數的值域只可能有五種情形：①｛0,1,2,…,n｝;②｛0,1,2,…,n,…，∞｝;③【0,1】;④［0,∞］;⑤｛0,∞｝。根據維數函數值域的情況，因子分別稱為Ⅰn型、Ⅰ∞型、Ⅱ1型、Ⅱ∞型及Ⅲ型的。前兩種因子又統稱為Ⅰ型的。其後的兩種統稱為 Ⅱ型的。Ⅰn型因子必定完全同構於B(hn)，其中hn 是n維希爾伯特空間。Ⅰ∞型因子必完全同構於B(H∞),其中H∞是某個無限維希爾伯特空間。Ⅰ型因子就是有極小非零投影的因子。設P是因子U中的投影，如果U中沒有P的真子投影P0使P比P0小,P就稱為U的有限投影。Ⅱ型因子就是沒有極小非零投影但有非零有限投影的因子。在Ⅰ型因子中，維數函數相當於投影的值域的維數，而Ⅱ型因子就好像其中投影的值域能夠連續地變化。馮·諾伊曼和默雷又用群測度空間構造的辦法（現在已成為標準的途徑），指出上述各種類型的因子都確實存在。他們又研究了所謂超有限的Ⅱ1型因子，即可以用有限維因子任意逼近的因子，證明了在完全同構的意義下這種因子是惟一的；並作出了兩個不完全同構的 Ⅱ1型因子。後來，陸續地又有人構造出相互不完全同構的 Ⅱ1型及Ⅱ∞ 型的因子。1967年，R.T.鮑爾斯受量子場論的啟發，證明了在無限維可分希爾伯特空間中，存在不可數個(連續統)相互不完全同構的Ⅲ型因子。隨後，不可數個(連續統)相互不完全同構的 Ⅱ1型因子及Ⅱ∞型因子也被人構造出來。這說明用維數理論所作的因子分類是很不完全的。在鮑爾斯發現互不同構的因子族后，H.阿拉基和E.J.伍茲提出了兩個不變數來分析有限維因子的無限張量積。1973年，A.孔涅發現這些不變數的簡單公式。並進而對馮·諾伊曼代數U引進了兩個不變數。孔涅用他引進的不變數對Ⅲ型因子作了更細緻的分類，提出了Ⅲλ型因子的概念，其中λ∈［0,1］。這種因子都是Ⅲ型因子，而且每個Ⅲ型因子必是某個Ⅲλ型因子。孔涅的理論使馮·諾伊曼和默雷在30年代作出而以後一直處於停滯不前狀態的因子分類理論獲得重要的發展，因而得到數學界的重視。

W*代數 如果A是個C*代數，而且A又可作為某個巴拿赫空間的共軛空間, 就稱A是W *代數。馮·諾伊曼代數必是W *代數，1956年證明：W *代數必與某希爾伯特空間的一個馮·諾伊曼代數同構。