蜂窩結構
用於航空航天等領域的設計方式
蜜蜂憑著上帝賦予它的智慧,選擇了角數最多的正六邊形。用等量的原料,使蜂巢具有最大的容積,因此能容納更大數目的蜂蜜。精巧神奇,而且十分符合現實需要,是一種最經濟的空間架構。蜜蜂建造的蜂巢,真是令人讚歎的天然建築物。早在18世紀初,法國天文學家馬拉爾地(Maraldi)(文獻)親自動手測量了許多蜂巢,發現每個蜂巢的孔洞和底部都是正六稜柱狀。
如果將整個蜂巢底部分為三個菱形截面,則每個銳角和每個鈍角的角度相等(銳角約為72°、鈍角約109°)。更令人驚奇的是,蜜蜂為了防止存蜜外流,每一個蜂巢的建築,都是從中間向兩側水平展開;每個蜂房從內室底部到開口處,都呈現13°的仰角。

蜂窩結構
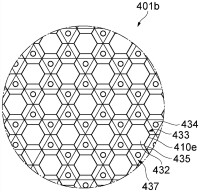
蜂窩結構
夾芯層形似蜂窩的一種夾層結構,又稱蜂窩夾層結構。
美國B-2隱形轟炸機的機體元件,多採用三明治結構,即在兩塊高強度薄板間,膠合密度甚低的蜂巢層,使機體強度增高、質量減輕。發動機的噴嘴是深置於機翼之內,呈蜂巢狀,使雷達波只能進、不能出。鉛筆中的石墨是由碳原子,排成六角形蜂巢狀的薄片組成。如果重新組合這些碳原子,就可以變成鑽石。
蜂窩式航天器
蜂窩的結構給航天器設計師們很大啟示,他們在研製時,採用了蜂窩結構:先用金屬製造成蜂窩,然後再用兩塊金屬板把它夾起來就成了蜂窩結構。這種蜂窩結構強度很高,重量又很輕,還有益於隔音和隔熱。因此,當前的太空梭、人造衛星、宇宙飛船在內部大量採用蜂窩結構,衛星的外殼也幾乎全部是蜂窩結構。因此,這些航天器又統稱為蜂窩式航天器。
蜂窩夾層結構
蜂窩結構
這種結構的夾芯層是由金屬材料、玻璃纖維或複合材料製成的一系列六邊形,四邊形及其他形狀的孔格,在夾芯層的上下兩面再膠接(或釺焊)上較薄的錶板。早期使用的輕質巴薩木夾層不耐潮,抗腐性差,不耐火,人們遂把注意力轉向金屬蜂窩夾層。1945年試製成最早的蜂窩夾層結構。蜂窩結構比其他夾層結構具有更高的強度和剛度,與鉚接結構相比,結構效率可提高15%~30%。夾層的蜂窩孔格大小、高矮及其構成格子的薄片厚度等決定錶板局部屈曲、孔格壁板屈曲的臨界應力及夾層結構的保溫性能。這些尺寸的選擇,一般要保證能夠承受一定的屈曲載荷的前途下具有一定的保溫性能。蜂窩結構的受力分析與一般夾層結構相同。在航空航天工業中,蜂窩結構常被用於製作各種壁板,用於翼面、艙面、艙蓋、地板、發動機護罩、尾噴管、消音板、隔熱板、衛星星體外殼、剛性太陽電池翼、拋物面天線、火箭推進劑貯箱箱底等。

蜂窩結構
蜂窩結構
T:目標區域;
t:正方形目標區域的邊長;
r:節點的感知距離;
N:初始節點集合;
r:節點總數;
:目標區域內的節點密度;
p:節點;
:節點P的感知區域;
:節點P的感知區域的圓周;
P:節點集合;
R(P):節點集合P的覆蓋區域, ;
E(P):節點集合屍的覆蓋區域的邊集合;
V(P):節點集合屍的覆蓋區域的頂點集合;
所得覆蓋集的大小
定義1:給定目標區域T和節點集合N,若T R(N),則稱N是一個覆蓋集。若W N且W是一個覆蓋集,則稱W是N的一個覆蓋子集。若W“在N的所有覆蓋子集中具有最小的尺寸,則稱W“是N的一個最小覆蓋子集。無線感測器網路覆蓋問題即是對於給定的目標區域T和節點集合N,尋找N的一個最小覆蓋子集W*。
在求出N的最小覆蓋子集W“后就可僅調度W“中的節點工作,W*中節點的感知區域就可完全覆蓋目標區域,而讓其他節點休眠,以減少網路的整體能量消耗。當W*中的節點失效后,可重新生成最小覆蓋子集。此外某些研究工作的目標是構造一個最小連通覆蓋子集,即不但要求活動節點能夠完全覆蓋目標區域,還要求活動節點是連通的,以保證活動節點之間的相互通信。相對於覆蓋性,節點集合的連通性容易得到滿足。在節點的通信距離大於2倍感知距離時,即可保證覆蓋子集一定是連通的,而一般情況下節點的通信距離要比感知距離大得多。即使節點的通信距離小於2倍感知距離,也可先求出覆蓋子集,再加入若干使之連通的節點.。易知,當且僅當初始節點集合是覆蓋集時才存在最小覆蓋子集。求解最小覆蓋子集己被證明是一個NP難問題,目前不存在多項式時間的有效演演算法。在感測器節點數目較多時只能通過近似演演算法得到接近最優解的覆蓋子集。
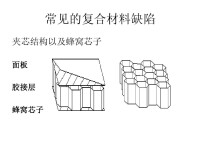
圖1顯示蜂窩結構的一部分,每個節點的有效覆蓋區域是一個大小相等的正六邊形,這些正六邊形可無縫覆蓋二維平面。在蜂窩結構中,每個節點都有6個鄰居,其感知區域的圓周正好被這6個鄰居完全覆蓋,且被每個鄰居覆蓋的角度為。若P為二維平面上的一個點集,易知E(P)中的元素必為圓弧,V(P)中的元素必為圓之間的交點。

蜂窩結構
可通過圖2所示的迭代方法構造蜂窩結構:圖2(a)在 上任選一點x,則E({x})中的唯一元素是角度為 的弧,V(P)= ;圖2(b)在 上選擇一點y,使得E({x})中的弧被 覆蓋 角度,同時 也被R({x})覆蓋 角度,V (P)={V1,Vz};圖2 (c)在 上選擇一點z,使得 覆蓋V (P)中某點,且E({x,y})中的弧被 覆蓋 角度,同時 也被R({x,y})覆蓋 角度。可重複此過程直至所選點集的覆蓋區域擴展至整個目標區域。在每一階段,若之前己選的點集為P,當前所選的點為p,則應滿足以下條件:
1)若V (P) ,則 應至少能覆蓋V(P)中某個交點,以使得E(P)中相應弧的端點被 覆蓋,加入P后該弧不會被分為兩段;
2)若E(P)中的某弧e與 相交,則e被 覆蓋的角度為,被R (P)覆蓋的角度為,這裡 為E(P)中與 相交的弧數。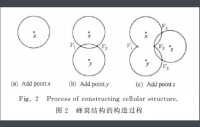

蜂窩結構
