折射角
折射光線與法線的夾角
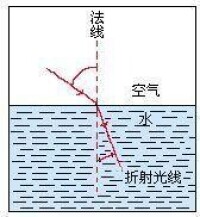
折射光線與法線的夾角叫折射角。其折射情況遵循折射定律。
﹙1﹚折射光線,入射光線和法線在同一平面內;
﹙2﹚折射光線和入射光線分居在法線兩側;
現實應用:從空氣看水中的物體,或從水中看空氣中的物體看到的是物體的虛像,看到的位置比實際位置高。
折射規律分三點:(1)三線一面,(2)兩線分居,(3)兩角關係分三種情況:①入射光線垂直界面入射時,折射角等於入射角等於0°;②光從空氣斜射入水等介質中時,折射角小於入射角;③光從水等介質斜射入空氣中時,折射角大於入射角(但存在於空氣中的角總是一個大角)。
折射定律的數學表達式為
其中,i是入射角,γ是折射角,是兩種介質中的光速。
。
其中,n就是折射率。
對於兩種不同的透明材料,將折射率定義式的變形代入折射定律,並約掉真空光速c,我們有
。
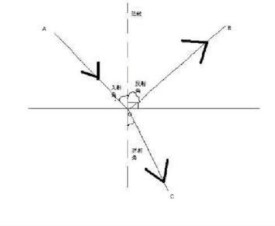
費馬原理又稱為“最短時間原理”:光線傳播的路徑是需時最少的路徑。費馬原理更正確的版本應是“平穩時間原理”。對於某些狀況,光線傳播的路徑所需的時間可能不是最小值,而是最大值,或甚至是拐值。例如,對於平面鏡,任意兩點的反射路徑光程是最小值;對於半橢圓形鏡子,其兩個焦點的光線反射路徑不是唯一的,光程都一樣,是最大值,也是最小值;對於半圓形鏡子,其兩個端點Q、P的反射路徑光程是最大值;又如最右圖所示,對於由四分之一圓形鏡與平面鏡組合而成的鏡子,同樣這兩個點Q、P的反射路徑的光程是拐值。
假設,介質1、介質2的折射率分別為,光線從介質1在點O傳播進入介質2,為入射角,為折射角。
由於介質會減緩光線的速度,折射率都大於1。
從點Q到點P的傳播時間為
.
根據費馬原理,光線傳播的路徑是所需時間為極值的路徑,取傳播時間T對變數x的導數,並令其為零。經整理后,可得。
將傳播速度與折射率的關係式代入,就會得到折射定律:。
假設入射波是頻率為ω的單色平面波,則為了在任意時間滿足邊界條件,反射波、折射波的頻率必定為ω。設 的形式為
其中,分別是入射波、反射波、折射波的波矢量,分別是入射波、反射波、折射波的波幅(可能是復值)。
為了在邊界任意位置滿足邊界條件,相位變化必須一樣,必須設定
。因此,。
不失一般性,假設,則立刻可以推斷第一定律成立,入射波、反射波、折射波的波矢量,與界面的法線共同包含於入射平面。
從波矢量x-分量的相等式,可以得到。
應用折射率的定義式:,
可以推斷第三定律成立: 。其中,n、θ分別是折射介質的折射率與折射角。
從入射波、反射波、折射波之間的相位關係,就可以推導出幾何光學的三條基礎定律。
一般來說:對同一束光,。
費馬原理:光在傳播過程中遵循“光程最短”的原則(也就是傳播最快)。據此,可以用數學的方法可以證明折射的規則:
。式中,i是入射角,γ是折射角,是兩種介質中的光速。
又因真空中的光速c最大且恆定,故規定,n就是折射率。
顯然,有
證明過程:下面我就來說說光為什麼這樣傳播:
一束光線由空氣中A點經過水麵折射後到達水中B點,已知光在空氣和水中傳播的速度分別是v1和v2,光線在介質中總是沿著耗時最少的路徑傳播。試確定光線傳播的路徑。
設A點到達水面的垂直距離為,B點到水面的垂直距離為,x軸沿水面過點O、Q,其中OQ的長度為l。
由於光線總是沿著耗時最少的路徑傳播,因此光線在同一介質內必沿著直線傳播。設光線的傳播路徑與x軸的交點為P,,則光線從A到B的傳播路徑必為折線APB,其所需要的傳播時間為:
.
下面來確定x滿足什麼條件時,T(x)在上取得最小值。
由於
註釋:T'(x)為T(x)的一階導數
為T(x)的二階導數
,又T'(x)在[0,l]上連續,故T'(x)在(0,l)內存在唯一零點x0是T(x)在(0,l)內的唯一極小值點,從而也是T(x)在[0,l]上的最小值點。
設x0滿足,即
記
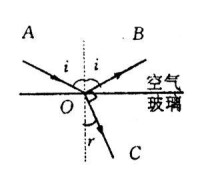
光照射到空氣與玻璃界面時發生的反射與折射現象
這就是說,當P點滿足以上條件時,APB就是光線的傳播路徑。上式就是光學中著名的折射定律,其中分別是光線的入射角和折射角。
一般來說:空氣中的折射角>玻璃中的折射角>水中的折射角