結合公理
結合公理
結合公理(axiom of incidence)是基本的幾何公理之一,亦稱關聯公理或從屬公理,是規定基本對象點、直線、平面之間從屬關係的一組公理,是希爾伯特公理系統中的第Ⅰ組公理。
結合公理包含8條結合公理:
Ⅰ.對於任意兩個不同的點A和B,至少有一直線a連結A和B。
Ⅰ.對於任意兩個不同的點A和B,至多有一直線a連結A和B。
Ⅰ.任一直線上至少存在著兩個點,又至少存在著不在同一條直線上的三個點。
Ⅰ.任給不在同一條直線上的三個點A,B,C,至少存在一個平面通過A,B,C,又任一平面上至少有一個點。
Ⅰ.任給不在同一條直線上的三個點A,B,C,至多存在一個平面通過A,B,C。
Ⅰ.如果一條直線上的兩個點落在同一個平面上,則該直線上的任何一點都落在該平面上。
Ⅰ.如果兩個平面有一個公共點,則它們至少還有另一個公共點。
Ⅰ.至少存在著四個點,它們不在同一個平面上。
應當指出,在上述8條結合公理中,僅有少數幾條出現在《幾何原本》中,大部分是德國數學家希爾伯特(D.Hilbert)補入的。因為歐幾里得(Euclid)和歷史上不少幾何學家在自己的論證中持有空間直覺觀念,例如,他們總是直覺地認為直線上必有無窮多個點,而且既不將此列為公理,又在論證中無條件地承認並使用它。在這個系統里,它可作為一條定理證明之,由於公理應儘可能少,故也不必將此列為公理。
Ⅰ1.對於任意兩點A,B,存在一條屬於這兩點A,B中每一點的直線a。
Ⅰ2.對於兩點A,B,存在不多於一條屬於這兩點A,B中每一點的直線。
我們說兩點三點(或對於直線、平面來說),意思是永遠指不同的諸點(或直線、平面) 。
在這裡希爾伯特為今後的正確理解起見,作出非常重要的註釋:
“術語‘屬於’我們也有時用其他的說法代替。例如我們不說直線a屬於A,B兩點中的每一點而說直線a通過兩點A,B,或者說直線a連接點A和點B,不說A屬於a,而說A在a上,或者說A是a(上)的一點,以及其他說法,如果點A在直線a上,又在直線b上,我們也說直線a和b相交於點A,或者說有公共的點A等等”。
不要以為我們在這裡是在解釋“屬於”這一術語了,這不過是以其他的詞句“在......上”,“(通)過”等代替這個不定義的術語而已。但除了這些詞句以外——而且這一點才是事情的本質——不要把任何同“屬於”等效的直觀概念糾纏在一起。
或者也可以完全避免上述的術語,只簡單地用文字記錄上述的術語。例如,對於任意兩點A,B常存在一直線a,A,B之中的每一點和a有著關係。
這樣說或者更好些:對於第一類的任何二對象A,B常有第二類的一對象a,它們有著關係。
或者,再簡略些說:對任意二點A,B,常存在這樣的a,使得。
正像在代數中文字和運算的符號可以有各式各樣的具體意義一樣,在抽象幾何中基本對象及其基本關係也有相同的情形。
在這裡要提出的唯一要求是須遵守若干規則或滿足若干公理。
Ⅰ3.在一直線上至少存在兩點,至少存在不在一直線上的三點。
Ⅰ4.對於不在一直線上的任意三點,存在屬於三點A,B,C中每一點的平面,對於任一平面常存在屬於它的一點。
Ⅰ5.對於不在一直線上的任意三點,存在屬於三點A,B,C中每一點的平面不多於一。
Ⅰ6.若直線a上有兩點A,B在平面 上,則直線a上任一點都在平面 上。
Ⅰ7.若二平面 有一公共點A,則它們至少還有另外一公共點B。
Ⅰ8.至少存在不在一平面上的四點。
這是第一組公理最後的一個公理。公理 Ⅰ1~ Ⅰ3叫做第一組的平面公理; Ⅰ4~ Ⅰ8叫做第一組的空間公理。
為了部分地解釋希爾伯特的觀點並且了解基本對象問題提法的實質起見,我們來看一個例題。因為“點”、“直線”和“平面“可以表示有任何本性的對象,只要它們適合公理,那麼我們假定四“點”A,C,B,D是通常的歐氏平面上的點,並且假定其中任意三點都不在一直線上,此外,還假定“不在一直線上”以及對象“直線”的字義正是我們在中學校中所習慣的。
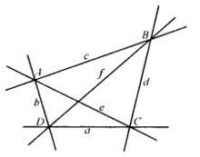
圖1
我們作一個模型,首先,第一類的綦本對象—— “點”——只容許有四個點A,B,C,D,任何其他的東西不算作“點”,六條直線認為是第二類的基本對象(第二類的東西)——“直線”。任何其他的東西不算作“直線”,我們限於用第一組的 Ⅰ1~ Ⅰ3三個公理,因此第三類的慕本對象——“平面”不再計入。這樣,有了四個第一類的對象——四個”點”——和六個第二類的對象——六條“直線”。
其次,因為在希爾伯特的公理法中基本關係“在……上”可以隨意指什麼,只要滿足公理就可以,那麼我們給這個詞以這樣的意義:令“點”A,B對應於“直線”a,而寫作:,同理有:,今約定在建立好的對應中每兩“點””(決)定”一直線。於是,在我們的約定之下公理 Ⅰ1是正確的:”二不同點常定一直線”。例如,點B,D定一直線e,倘若不說B,D“定”一“直線”e,而按照希爾伯特的說法,要說點B和D“在”“直線”e“上”。反過來,如果說二不同點B,C”在”“直線”“b”“上”,意思是說,“直線”b由“點”B和C所定。總之這都需要基本關係“在……上”,這種關係的直覺概念也可以和我們一般用的不一致,我們也可以說“直線”b“(通)過”“點”B和C。“通過”一語必須使具有和第一個公理的內容有等效的含義,等等。
容易看出,在我們的模型中公理 Ⅰ2成立,一直線一般只“含有”兩“點”,是的,直線a“含有”A,B兩“點”,按照希爾伯特的說法,假如A是一點,它和另一點定直線a,說是:A“在”a“上”,A“是”a“的上點”。是的,在我們的模型中A“是”“直線”“a上“的點”,因為A和B共同“定”a。完全一樣地,A“是”“直線”d上“的點”。希爾伯特還說:“如果A‘在’直線a'上’,又在另一直線b上,我們就說‘直線’a和b'有公共點'A”。是的,在我們的模型中“直線”a和d“有公共點”A,也可以這樣說:“直線”a和d“交於”點A。
在我們的模型中公理 Ⅰ3也是實現的:“在一直線上至少存在兩點;在每一平面上至少存在三個不在一直線上的點”。是的,在我們的模型的對象中“在每一直線上至少存在兩點”。例如,在直線上存在點A和C,在我們的模型中所有的“點”和“直線”可以認為屬於一“平面”。因此公理 Ⅰ3的第二部分是實現的:點A,B,C不“在”一直線“上”。
我們就以這個模型對於第一組所有的平面公理都成立作結束,現在我們轉而談談從代數中類似的情形來弄清問題的要點。如果在代數中寫下公式,則文字可以代替任何數值,這公式依然成立。同樣,在希爾伯特的公理法中基本概念“點”、“直線”、“平面”可以換成有任何本性的對象,只要這些公理仍舊成立即可。如果在上面的等式中把關係“+”、“=”理解為向量代數里的符號,而a和b是向量,這公式還是成立的。完全相仿地,在希爾伯特的公理法里,不僅基本對象,還有對象間的基本關係都可以理解為有任何本性的對象和任何對象的關係,只需滿足公理就成了。例如,在上面所講的模型中有四個普通的點和六條直線,但關係“在……上”完全跟普通的意義不同。
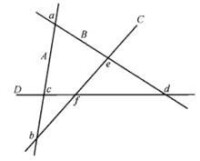
圖2
建立了這種對應之後,我們便認為在第一組的平面公理中術語“定”與術語“對應”只能在上述的意義下等效。這樣一來,“點”A和B定“直線”f;A,D定“直線”e。按照希爾伯特的說法,應該說:“點”A,B“在直線”f“上”;“直線”f‘‘通過點”A,B;A和B“是直線”f“的點”,等等。
因為在所做的模型中“直線”a和c同時“含有”“點”C,也就是“點”C“在直線”a和c“上”,所以可以說“直線”a和c“交於”一“點”C,在這個模型中所有第一組的平面公理都滿足。
注意,所討論的模型只服從公理 Ⅰ1~ Ⅰ3,其餘的公理 Ⅰ4~ Ⅰ8對這個模型不生效;其餘組的公理也不成立,可以當作是一些例外。