共找到2條詞條名為可數集的結果 展開
- 能與自然數集N一一對應的集合
- 可列集
可數集
能與自然數集N一一對應的集合
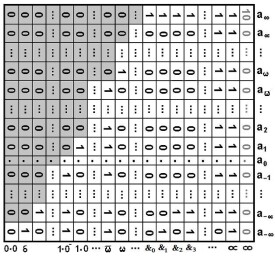
可數集(countable set),是能與自然數集N建立一一對應的集合,又稱可列集。如果將可數集的每個元素標上與它對應的那個自然數記號,那麼可數集的元素就可以按自然數的順序排成一個無窮序列a1,a2,a3,…an,…。比如全體正偶數的集合是一個可數集,全體正奇數的集合也是可數集,它們與自然數集可以建立如下的一一對應。
可數集的一個定義是“能與自然數集的某個子集一一對應的集合”。在這個意義下不是可數集的集合稱為不可數集。這個術語是康托爾創造的。可數集的元素,正如其名,是“可以計數”的:儘管計數可能永遠無法終止,集合中每一個特定的元素都將對應一個自然數。 “可數集”這個術語也可以代表能和自然數集本身一一對應的集合。兩個定義的差別在於有限集合是否被視為可數集。為了避免歧義,前一種意義上的“可數”有時稱為“至多可數”,后一種“可數集”則又稱為“無限可數集”。
可列和可數在英文里是一個詞:countable,這是以前科學不夠發達,不需要進行區分時的結果。而我們需要進行概念區分,因此按字面意思,將“可列”理解為“可以寫出”;“可數”理解為“可以記數”。在下面的論述中,分這樣兩個概念討論。我們無法寫出一個最大的自然數,因此自然數全體是不可寫全的,任何無限集,都是不可寫全的。如果有一些數,位數多的我們承認有生之年無法完全比較,而在可比較的範圍內它們又一樣,這樣我們在數元素個數時,不知道它們該算一個元素還是多個元素,這種情況,稱為不可記數。
從定義可以看出,不可寫全的數,如果我們發現它的一部分,和集合中的其它元素都不一樣,我們就知道它是一個獨立元素,就可以記數。而不可記數的數,我們可能可以知道它的數量範圍(最大數量每個算一個元素,最小數量認為只有一個元素),或者也可以知道它們都是可寫的。因此這兩個概念是有交叉而互不影響的。無理數除了能用有理數表示的和可以定義的,都是不可列的。
定理:最大元素數量的有限集(如果存在的話),或與最大數量有限集差固定常數的集合(如果仍然存在的話),是不可能寫全的。最大元素數量有限集是無限趨近於無限集的,以至於沒有手段進行判斷。任何定義的無限集或有限集都需要滿足此公理。
證明:假設最大有限集元素被全部寫出,那麼寫完其中所有元素后,再增加一個元素,該集合元素數量還是有限的,但元素數量比已寫出的集合元素數量多1,證明原來假設寫出的是數量最多的有限集不成立。所以最大元素數量的有限集,是不可能寫全的。假設與最大數量有限集差固定常數的集合被全部寫出,那麼再寫該常數多個元素,就能寫出最大有限集,這與剛才的結果矛盾。
定理:位數最多的非無限循環有理數(如果存在的話)是不可能被寫出的,儘管它的定義是有有限位,但它是無限趨近於無理數的,以至於沒有手段進行判斷。
證明:假設位數最多的非無限循環有理數被寫出,我們在這個數的最後再加一位,這個數還是有限位有理數,但位數比已寫出有理數多一位,證明原來寫出的不是位數最多的非無限循環有理數。所以位數最多的非無限循環有理數是不可能被寫出的。
0,1,2,3,4,5,6,n,
根據定義,自然數集顯然是可數集。
注意一個可數集“可數”的方式不一定唯一,如下面也是自然數集和自身的一一對應:
1,0,2,3,4,5,6,7,8,9,……(以下按順序排列)

可數集
6,5,4,3,2,1,0,7,8,9,……(以下按順序排列)
1,0,3,2,5,4,7,6,9,8,……(以下按規律排列)
0,2,4,6,8,10,12,2n,
非負偶數組成的集合是一個無限可數集,由上面列舉的順序即可看出對應關係:非負偶數2n對應自然數n。
1,3,5,7,9,11,13,,
同理,非負奇數對應自然數n。
這說明一個可數集可以含有可數的真子集,反過來,兩個可數集也可以並成一個可數集。
0,1,-1,2,-2,3,-3,
儘管看起來比自然數集“大”,整數集依然是可數的。
0,1/1,-1/1,2/1,-2/1,1/2,-1/2,3/1,-3/1,3/2,-3/2,1/3,-1/3,2/3,-2/3,4/1,-4/1,4/3,-4/3,1/4,-1/4,3/4,-3/4,5/1,-5/1,
整數集與有理數集都是可數集。按照基數概念,能一一對應的兩個集合的基數相同,於是有理數集、整數集、全體正偶數集等與自然數集有相同的基數。在這個意義上說,這些集合所含元素是“一樣多”,但這些集合又是一個包含另一個作為真子集,所以又不同於有限集元素的“多少”概念。值得注意的是,並非所有的無窮集都是可數集,因為G.康托爾證明了實數集不是可數集,這樣,實數集與自然數集有不同的基數,因而說明了無窮集所含元素數量的多少還有某種層次區別。
∅,{1},{2},{1,2},{3},{1,3},{2,3},{1,2,3},{4},
注意到任何正整數集的有限子集都有有限的最大元素,可證。
空序列,(1),(2),(1,1),(1,2),(2,1),(2,2),(3),(1,3),(2,3),(3,3),(1,1,1),(1,1,2),(1,1,3),(1,2,1),……(3,3,3),(4),(1,4),……,(4,4),(1,1,4),……,(4,4,4),(1,1,1,1),……,(4,4,4,4),(5),
注意到任何正整數的有限長度序列都有有限的最大元素和有限的項數,從而可以取二者的較大值,可證。
可數集的子集是至多可數的。

等勢的集合叫做可數集
有限多個可數集的並集是可數的。
在承認可數選擇公理的前提下,可數多個可數集的並集是可數的。
有限多個可數集的笛卡爾積是可數的。
對集合S,下面3種說法等價:
1、S至多可數,即存在S到自然數集的單射;
2、S為空或存在自然數集到S的滿射;
3、S為有限集或存在自然數集與S間的雙射。
值域為可數集的單射,其定義域至多可數。
定義域為可數集的滿射,其值域至多可數。
可列和可數在英文里是一個詞:countable,這是以前科學不夠發達,不需要進行區分時的結果。
我們無法寫出一個最大的自然數,因此自然數全體是不可寫全的,任何無限集,都是不可寫全的。(不可列)
無理數除了能用有理數表示的和可以定義的,都是不可列的。
可能上面的幾個“如果存在的話”看起來是荒謬的,但是數學中總是有這樣的情況:應用了不同的公理和不同的定義,就能得到不同的結果,有些說不定是有用的,例如黎曼的非歐幾何,現在成為了廣義相對論的基礎。如果有新定義說“可數”也是一種“有限”呢。在有些情況下這是合理的。
集合比較的等勢概念,並非統一公認的,很多數學家對此進行了質疑。康托爾對實數集不是可數集的證明,也是被質疑的證明。