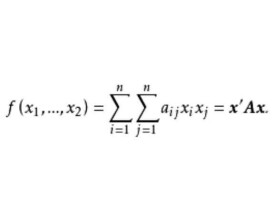實二次型
實二次型
實二次型(real quadra ticform)是一類重要的二次型，指實數域上的二次型，任意實二次型f(x₁，x₂，…，xn)都可以通過實滿秩線性代換化為形如y²1+…+y²p-y²p+1-…-y²r的標準形。這種標準形稱為實二次型f的規範型或正規型，其中r是f的秩，正平方項個數p稱為f的正慣性指數，負平方項個數q=r-p稱為f的負慣性指數，s=p-q稱為f的符號差，實二次型的正、負慣性指數是惟一確定的，此稱為實二次型的慣性定律，亦稱慣性定理。此定理由西爾維斯特(J.J.Sylvester)給出，故亦稱西爾維斯特定理。但他認為不證自明。雅可比(C.G.J.Jacobi)也獨立發現並證明了這個定理。兩個n元實二次型等價的充分必要條件是：它們有相同的秩，且有相同的正慣性指數(或有相同的秩與符號差)。
(1)n元實二次型指的是含有n個變數的實係數二次齊次多項式
其中為n階實對稱矩陣。
對於取定的變數組來說,n元實二次型與n階實對稱矩陣是互相唯一確定的，稱A是二次型f的矩陣，稱f是以A為矩陣的二次型。
(2)只有平方項而沒有交叉項,的二次型稱為n元標準二次型
其中
(3)如果對於n階方陣A和B，存在n階可逆矩陣P使，則稱A與B合同，記為。矩陣之間的合同關係有反身性、對稱性和傳遞性。
(4)所有平方項的係數為±1或0的標準二次型稱為規範二次型
其中r是二次型的秩，k為二次型的正慣性指數，r-k為二次型的負慣性指數，為二次型的符號差。
(1)對於任何變數值，二次型的值恆為0。
(2)n階方陣A和B等價指的是存在n階可逆矩陣P和Q使得，記為。
n階方陣A和B相似指的是存在n階可逆矩陣P使得，記為。
n階方陣A和B合同指的是存在n階可逆矩陣P使得，記為。
兩個相似的矩陣一定是等價的，兩個合同的矩陣也一定是等價的。但是，反之並不成立，即等價的矩陣未必相似，也未必合同，矩陣相似與矩陣合同是兩個不同的概念，只有當中的P是正交矩陣時，才同時有，所以，兩個矩陣正交相似與正交合同是一回事。
(3)對於任意一個n元實二次型，必存在正交變換,這裡P是n階正交矩陣，把它化為標準形：
其中，就是對稱矩陣A的n個特徵值。
(4)對於任意一個n元實二次型，必存在可逆線性變換，這裡Q是n階可逆矩陣，把它化為標準形
其中,未必是對稱矩陣A的特徵值。
(5)慣性定理對於任意一個n元實二次型，必存在可逆線性變換，這裡R是n階可逆矩陣，把它化為規範形
其中k和r是由A唯一確定的(與所採用的變換的選擇無關)。
慣性定理的矩陣形式。對於任意一個n階對稱矩陣A，一定存在n階可逆矩陣R使得
其中k和r是由B唯一確定的。
(6)合同判別法。當A與B是同階對稱矩陣時，它們合同當且僅當它們有相同的秩和相同的正慣性指數，因為對稱矩陣的秩就是它的正慣性指數和負慣性指數之和，所以，兩個同階對稱矩陣A與B合同當且僅當它們有相同的正慣性指數和相同的負慣性指數。
基本信息
- 中文名
- 實二次型
- 外文名
- real quadratic form
- 所屬學科
- 數學
- 所屬問題
- 高等代數(二次型)
- 簡介
- 實數域上的二次型