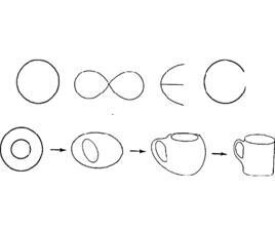拓撲等價
拓撲等價
拓撲等價(topological equivalence)有多個解釋,一個是刻畫微分方程的解之間的關係的重要概念;另一個是指對連續流進行分類的一種方法;還有一個是說幾個圖形,如果其中任一個可以通過拓撲變換從其餘圖形得到,就稱它們為拓撲等價的,或稱幾個圖形,其中每一個可以從其餘任一個圖形經扭轉、彎曲、拉長或收縮得到,而不出現任何點的重疊與斷開,它們就是拓撲等價的。例如,一個籃球拓撲等價於一個足球。
拓撲等價是刻畫微分方程的解之間的關係的重要概念。如果對微分方程系
存在向量函數滿足下列條件,則稱為拓撲等價:
1. 當 時, 一致地成立,且 一致地成立;
2. 對於 定義為 是同胚映射;
3.定義為 也具性質1;
4. 若 是 的解,則 是 的解;若 是(2)的解,則 是(1)的解。
設 和 在R上連續,如果有常數,只要 ,使線性系統
與線性系統拓撲等價,那麼,稱 具有結構穩定性。有界線性系統具有結構穩定性的充分必要條件是它自己具有指數型二分性。
拓撲等價是指對連續流進行分類的一種方法,設φ,ψ分別是拓撲空間M,N上的連續流,若存在同胚 ,使得對任意,h把φ過的軌道保向地映射到ψ過 的軌道上,就稱φ和ψ是拓撲等價的。拓撲等價這一關係是一個等價關係,拓撲等價從拓撲的觀點刻畫出兩個連續流的軌道結構是相同的,因此,連續流的結構穩定性是用拓撲等價來揭示的。
一個立體球拓撲等價於一個立方體或任何正則立體,三維歐幾里得空間中的兩個圖形稱做拓撲等價的,當且僅當存在一彈性運動,使得其中一圖形與另一圖形重合。當然如果我們給出兩個物理客體,其中一個是固體橡膠球,另一個是固體的木製立方體,我們不能使橡膠球與木立方體重合,如果我們想使它們重合,它們就得互相撞擊,使得橡膠球平貼在立方體的外表面上而不通過立方體的內部。這一例子可以用來強調數學所研究的圖形——無論是在歐幾里得幾何中還是在拓撲學中——不是物理客體,而是抽象圖形。一個三角形不是可以用木頭、紙張或繩子做成的東西,它是由以某種方法安放在一起的“線段”構成的,而線段又是“點”的某種組合,這樣,對幾何或拓撲進行任何認真的研究,就需要一個適當的基礎知識,即對點集合進行一些討論,並清楚地理解怎樣使一個點集與另一個點集重合,現在,我們仍然依靠對圖形的拓撲等價的直覺,它是建立在理想彈性圖形的彈性運動上的。(後文圍繞這一定義展開)。
下面將討論我們感興趣的幾個標準圖形。
一個圓是一平面曲線,它上面的每一點與平面上一定點的距離為某一定長,這一定點就是圓心,定長即圓的半徑,一單純封閉曲線乃是與圓拓撲等價的曲線,一個單純封閉曲線可以在一個平面上也可以不在一個平面上,圖1給出不在一平面上的打結的單純封閉曲線的例子。
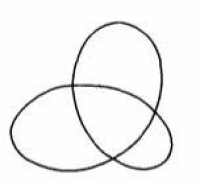
圖1
一個球面是一個三維的表面,它上面所有的點與某一定點的距離為某一定長,這個定點即此球面的球心,這個定長即此球面的半徑。
一個開圓球是三維空間中被某一球面所圍住的那部分,但不包括球面本身,一個閉圓球是三維空間中某一球面的內部或球面上的那部分(即球面上所有的點都在閉圓球上),注意,無論開圓球還是閉圓球都是三維空間里的一個立體,一個閉圓球是一個開圓球加上其內部為該開圓球的那個球面。
一個帶p個柄的球面乃是三維空間里這樣的一個表面:在一球面上鑿2p個洞,彎曲P個不同的管子,將它們的兩端分別插在這些洞里而得到的一個表面,圖2表示一個帶三個柄的球面。
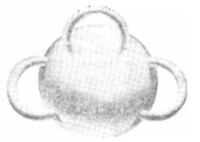
圖2

圖3
一個“胎形”(圖3)乃是三維空間里這樣的一個表面:將一個圓繞圓所在平面且不與此圓相交的直線旋轉而得到的一個表面,可以把胎形想成一個車輪的內胎或一個油炸圈餅的表面。
如果兩個圖形是拓撲等價的,我們可以用一彈性運動將一圖形變成另一圖形來證明之。例如,設有一圓形橡膠帶,我們可將它切斷,彎曲成圖1中曲線的形狀,然後再把兩端接成它們原來的樣子,這可以證明圖1中的曲線確實是一個單純封閉曲線,因為它拓撲等價於一個圓。
那麼怎樣證明兩個圖形不是拓撲等價的呢?這就需要證明不存在任何彈性運動,可將一個圖形變成與另一圖形重合。當然,我們不可能一一試用每種彈性運動——不同的彈性運動太多了,給出這類證明的一個方法是,找出其中一個圖形的一種性質,而這性質不為另一圖形所具備,如果這一性質是拓撲性質,那麼這兩個圖形就不可能是拓撲等價的,因為任何彈性運動都不能產生或消除這一性質,所以沒有一種彈性運動可使其中的一個圖形與另一圖形重合。我們證明一個球面不拓撲等價於一個胎形,以此為例說明這類證明過程,事實上,如果球面上面有一任意單純封閉曲線,並沿此曲線切割球面,則這個表面就分裂成兩部分,故球面上任意單純封閉曲線都使得這個球面不再是連通的,而胎形不具有這一性質。如果有一個圓穿過胎形的一個洞並圍繞著胎的橫切面,用這樣的圓曲線切割此胎形,這個表面就變成一根管子,但它仍然是一個整體,所以胎形不能被這樣的曲線切割成不連通的,故胎形不具有球面所具有的上述性質,而且,一個表面可以被它上面的任意單純封閉曲線切割成不連通的這一性質顯然是拓撲性質,於是,一個球面與一個胎形不拓撲等價。