共找到28條詞條名為回歸的結果 展開
- 數學術語
- 俄羅斯2003年安德烈·薩金塞夫執導劇情片
- 2019年薛曉路執導電影
- 西班牙2006年佩德羅·阿莫多瓦執導電影
- 漢語詞語
- 2017年電視劇
- 2013年唐靈隆導演電視劇
- 韓國2007年李圭滿執導電影
- 維多利亞·希斯洛普著長篇小說
- 尹濟均執導的電影
- 歌唱家金燦音樂作品
- 遊戲《三國志·曹操傳》人物技能
- 顧城創作詩歌
- 遊戲《英靈傳說SoL》術語
- 2002年西班牙墨西哥電影
- 中國工人出版社2014年出版作品
- 吳倩蓮演唱歌曲
- 胡月強創作小說集
- 彭鋒所著書籍
- 2018年電影
- 2012年微電影
- 2015年曾明山導演電影
- 桑布扎組合演唱歌曲
- 企業品牌
- 日沃因·帕夫洛維奇執導的電影
- 美國1980年Greydon Clark執導科幻電影
- 2008年楊子執導電影
- 韓國諾特劇團話劇《回歸》
回歸
數學術語
回歸,指研究一組隨機變數(Y1,Y2,…,Yi)和另一組(X1,X2,…,Xk)變數之間關係的統計分析方法,又稱多重回歸分析。通常Y1,Y2,…,Yi是因變數,X1、X2,…,Xk是自變數。回歸分析是一種數學模型。
回歸分析是一種數學模型。當因變數和自變數為線性關係時,它是一種特殊的線性模型。
最簡單的情形是一元線性回歸,由大體上有線性關係的一個自變數和一個因變數組成;模型是Y=a+bX+ε(X是自變數,Y是因變數,ε是隨機誤差)。
通常假定隨機誤差的均值為0,方差為σ^2(σ^2﹥0,σ^2與X的值無關)。若進一步假定隨機誤差遵從正態分佈,就叫做正態線性模型。一般的,若有k個自變數和1個因變數,則因變數的值分為兩部分:一部分由自變數影響,即表示為它的函數,函數形式已知且含有未知參數;另一部分由其他的未考慮因素和隨機性影響,即隨機誤差。
當函數為參數未知的線性函數時,稱為線性回歸分析模型;當函數為參數未知的非線性函數時,稱為非線性回歸分析模型。當自變數個數大於1時稱為多元回歸,當因變數個數大於1時稱為多重回歸。
回歸分析的主要內容有以下:
①從一組數據出發,確定某些變數之間的定量關係式;即建立數學模型並估計未知參數。通常用最小二乘法。
②檢驗這些關係式的可信任程度。
③在多個自變數影響一個因變數的關係中,判斷自變數的影響是否顯著,並將影響顯著的選入模型中,剔除不顯著的變數。通常用逐步回歸、向前回歸和向後回歸等方法。
④利用所求的關係式對某一過程進行預測或控制。
回歸分析的應用非常廣泛,統計軟體包的使用可以讓各種演演算法更加方便。
回歸主要的種類有:線性回歸、曲線回歸、二元logistic回歸、多元logistic回歸。
相關分析研究的是現象之間是否相關、相關的方向和密切程度,一般不區別自變數或因變數。而回歸分析則要分析現象之間相關的具體形式,確定其因果關係,並用數學模型來表現其具體關係。比如說,從相關分析中我們可以得知“質量”和“用戶滿意度”變數密切相關,但是這兩個變數之間到底是哪個變數受哪個變數的影響,影響程度如何,則需要通過回歸分析方法來確定。
一般來說,回歸分析是通過規定因變數和自變數來確定變數之間的因果關係,建立回歸模型,並根據實測數據來求解模型的各個參數,然後評價回歸模型是否能夠很好的擬合實測數據;如果能夠很好的擬合,則可以根據自變數作進一步預測。
例如,如果要研究質量和用戶滿意度之間的因果關係,從實踐意義上講,產品質量會影響用戶的滿意情況,因此設用戶滿意度為因變數,記為Y;質量為自變數,記為X。根據圖8-3的散點圖,可以建立下面的線性關係:
Y=A+BX+§
式中:A和B為待定參數,A為回歸直線的截距;B為回歸直線的斜率,表示X變化一個單位時,Y的平均變化情況;§為依賴於用戶滿意度的隨機誤差項。
在SPSS軟體里可以很容易地實現線性回歸,回歸方程如下:
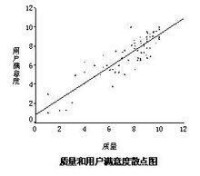
質量和客戶滿意度散點圖
上面所示的例子是簡單的一個自變數的線性回歸問題,在數據分析的時候,也可以將此推廣到多個自變數的多元回歸,具體的回歸過程和意義請參考相關的統計學書籍。此外,在SPSS的結果輸出里,還可以彙報R2,F檢驗值和T檢驗值。R2又稱為方程的確定性係數(coefficientofdetermination),表示方程中變數X對Y的解釋程度。R2取值在0到1之間,越接近1,表明方程中X對Y的解釋能力越強。通常將R2乘以100%來表示回歸方程解釋Y變化的百分比。F檢驗是通過方差分析表輸出的,通過顯著性水平(significantlevel)檢驗回歸方程的線性關係是否顯著。一般來說,顯著性水平在0.05以下,均有意義。當F檢驗通過時,意味著方程中至少有一個回歸係數是顯著的,但是並不一定所有的回歸係數都是顯著的,這樣就需要通過T檢驗來驗證回歸係數的顯著性。同樣地,T檢驗可以通過顯著性水平或查表來確定。在上面所示的例子中,各參數的意義如表1-1所示。
表1-1線性回歸方程檢驗
| 指標 | 值 | 顯著性水平 | 意義 |
| R | 0.89 | “質量”解釋了89%的“用戶滿意度”的變化程度 | |
| F | 276.82 | 0.001 | 回歸方程的線性關係顯著 |
| T | 16.64 | 0.001 | 回歸方程的係數顯著 |