球面三角
研究球面三角形邊角關係的學科
球面三角是研究球面三角形的邊、角關係的一門學科。從十六世紀起由於天文學、航海學、測量學等方面的發展,球面三角逐漸形成了獨立學科。從平面三角學我們知道,一圓周的1/360 ,叫做1度的弧。1度弧的1/60 叫做1角分的弧。1角分弧的1/60 叫做1角秒的弧。根據弧和所對圓心角的關係,可以得出角的量度。一圓周所對的圓心角為360°。因此,1度的弧所對的圓心角,叫做1°的角;1角分的弧相對的圓心角,叫做1′;1角秒的弧所對的圓心角,叫做1"。
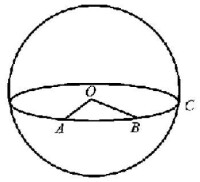
圖1 經過球面上任意兩點A、B可做一大圓
角和弧的量度單位,常用的有兩種:
弧度:長度和半徑相等的圓弧所對的圓心角,叫做1弧度(rad)。
由於一圓周的長度等於2π個圓半徑的弧長,根據以上弧度的定義,得到弧度和度的關係如下:
;
;
或者 ;
;
。
如果一個角的值以弧度表示時為θ,那麼以度表示時其值為;以角分表示時為;以角秒表示時為。為了方便起見,我們用符號θ°,θ′,θ"表示一個角的度數、角分數、角秒數。
。
當角度很小時,角度的正弦或正切常可以近似地用它所對的弧來表示。
例如:
由此得:
根據相同的理由,得:
上式常寫為:
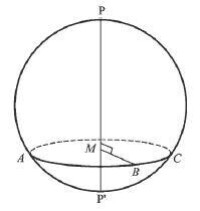
圖2球面上圓的極P與P’
例如通過圖1中的任意兩點A和B,也僅可以做一個大圓ABC。A、B兩點間的大圓弧(小於180°的那段弧)可以用線長、也可以用角度計量,在天文上常用角度來計量,叫做A、B間的角距,記為⌒AB(⌒應該畫在AB的上方,下同) ,它等於大圓弧⌒AB所對的中心角∠AOB。
球面上圓的極:設⌒ABC為球面上的一個任意圓(圖2),它所在的平面為MABC,又設PP’為垂直於平面MABC的球直徑,則它的兩個端點P和P’叫做圓⌒ABC的極。如果用一句話來表達,可以這樣說:垂直於球面上一已知圓(不論大圓或小圓)所在平面的球直徑的端點,叫做這個圓的極。
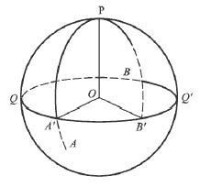
圖3球面角的量度
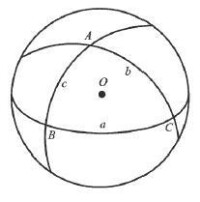
圖4球面三角形
從上面的討論可以概括出下述結果:如果以球面角的頂點為極作大圓,則球面角的邊或其延長線在這個大圓上所截取的那個弧段便是球面角的數值。
球面三角形:把球面上的三個點用三個大圓弧聯結起來,所圍成的圖形叫做球面三角形。這三個大圓弧叫做球面三角形的邊,通常用小寫拉丁字母a、b、c表示;這三個大圓弧所構成的角叫做球面三角形的角,通常用大寫拉丁字母A、B、C表示,並且規定:A角和a邊相對,B角和b邊相對,C角和c邊相對(如圖4所示)。三個邊和三個角合稱球面三角形的六個元素。
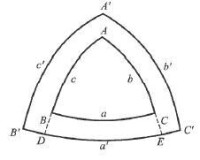
圖5極三角形
極三角形和原三角形有著非常密切的關係,這種關係存在著兩條定理。
定理1:如果一球面三角形為另一球面三角形的極三角形,則另一球面三角形也為這一球面三角形的極三角形。這條定理很容易證明,請讀者自證。
定理2:極三角形的邊和原三角形的對應角互補;極三角形的角和原三角形的對應邊互補。
證明:B'是b的極(圖F3.5),C'是c的極,所以有:
。
即
但由定理1,A是⌒B'C'的極,故有⌒DE=A,將此式以及'代人上式,便得到
(1.1)式即定理2的前半的證明。定理2的後半不需證明;因為實際上,它只是定理1和定理2的前半的一個推論。
1.球面三角形兩邊之和大於第三邊。
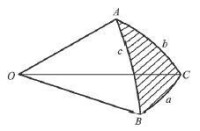
圖6球面三角形兩邊之和大於第三邊
推理:球面三角形兩邊之差小於第三邊。
2.球面三角形三邊之和大於0°而小於360°。
證明:因為a,b,c均為正,故,又由立體幾何得知凸多面角各面角之和小於360°,因此。
3.球面三角形三角之和大於180 °而小於540 °。
證明:由極三角形和原三角形的關係得:,即 。
但根據定理2有:。
所以上式化為。
除了上述三個基本性質以外,還有兩個重要的基本性質;對於這兩個性質,我們只寫出結果,而不給出證明。
4.若球面三角形的兩邊相等,則這兩邊的對角也相等。反之,若兩角相等,則這兩角的對邊也相等。
5.在球面三角形中,大角對大邊,大邊對大角。
下面我們要推導出六個基本公式,它們全是針對三個邊都小於90°的球面三角形導出的,但是能夠證明所得公式適用於任何球面三角形。
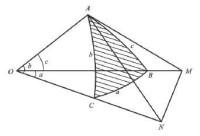
圖7推導餘弦公式的圖
過頂點A做b、c邊的切線,分別交OC,OB的延長線於N、M,由此得到兩個平面直角三角形OAM、OAN和兩個平面普通三角形△OMN、△AMN。
在平面三角形OMN中,應用平面三角的餘弦定理,得。
同理,在平面△AMN中,得.
因此,即或。
將,代入上式,便得到(1.2)式是a邊的餘弦公式,其他兩個邊的餘弦公式在形式上和(1.2)式完全一樣,可以用依次輪換邊和角的字母的方法而得出,所以從(1.2)式得到b邊的餘弦公式為cosb=cosccosa+sincsinacosB (1.3)
由(1.3)式得到c邊的餘弦公式為cosc=cosacosb+sina sinbcosC (1.4)
(1.2)式、(1.3)和(1.4)式合稱邊的餘弦公式,可以用文字表達為:球面三角形任意邊的餘弦等於其他兩邊餘弦的乘積加上這兩邊的正弦及其夾角餘弦的連乘積。
設球面三角形ABC的極三角形為A'B'C',則按照(1.2)式有。
因為 ,所以上式化為。即
利用輪換變更字母法,可以得出B角和C角的餘弦公式。(1.5)式就是角的餘弦公式,可用文字表達為:球面三角形任一角的餘弦等於其它兩角餘弦的乘積冠以負號加上這兩角的正弦及其夾邊餘弦的連乘積。
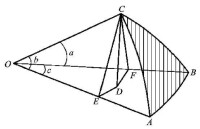
圖8推導正弦公式的圖
從圖8可得。因得 sina/sinA= sinb/sinB。利用輪換變更字母法,可以得出其它兩個類似的式子,最後得sina/sinA= sinb/sinB= sinc/sinC(1.6)
(1.6)式就是正弦公式,文字表達為:球面三角形各邊的正弦和對角的正弦成正比。
右邊的餘弦公式有:。
第二個式子可以改寫為:。
將第一個式子代入上式的右邊,得將上式兩端各除以sinc,便得到
同理,得
其他類似的式子可以從(1.7)式或(1.8)式,利用輪換變更字母法得出。(1.7)式或(1.8)式都是第一五元素公式,它具有一定的規律,但是它的文字表達式很繁瑣,因此這裡不寫出來。
利用極三角形和原三角形的關係(定理2),可以導出下列兩個公式:
其它類似的式子可以從(1.9)式或(1.10)式,利用輪換變更字母法得出,(1.9)或(1.10)式都是第二五元素公式。它的文字表達式也沒有必要寫出來。
把第一五元素公式和正弦公式聯合起來,可以導出球面三角形中相鄰的四個元素的關係式,即:
其他類似的式子,可以從(1.11)式或(1.12)式利用輪換變更字母法得出。
簡介
有一個角等於90°的球面三角形叫做直角球面三角形。設球面三角形ABC中,,且,將它們代入以上各公式,經過適當的變換,可得下列常用的直角三角形公式:
——(1.13)
納皮爾法則
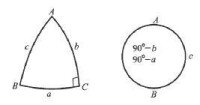
圖9用聶比爾定則記直角球面三角十公式
全球網格模型在全球空間資料庫、全球性問題研究和基於空間信息集成等方面具有潛在的應用價值,國內外學者對之開展了大量工作。全球網格構建主要採用下面3種方式(Whiteetal.,1992,1998,1999;Sahretal.,2003):第1種方式是在球面柏拉圖立體上直接剖分球面,如Sadourny等(1968)的剖分模型以及LianSong等(2000)所提出的小圓弧剖分模型等;第2種是循環剖分柏拉圖立體的弦,然後映射到球面,如Dutton(2000,1996,1998)所提出的QTM模型等;第3種均勻剖分展開在柏拉圖立體各面的地圖投影,如Snyder(1989)多面體投影族、Fekete(1990a,b)提出的SQT模型(該模型實質上是一種Gnomonic投影剖分(Snyder&Voxland,1989))、Fuller-Gray投影(Gray,1995,1994)等,然後反投影到球面。3種方法各有優缺點。其中Sadourny及Dutton的QTM模型頂點在球面上的分佈具有確切的映射位置,但邊界模糊,缺乏明確的數學定義,直接影響模型的實際應用。Dutton利用ZOT投影將正八面體投影到平面上,轉換為由平面直角三角組成的正方形網格,通過遞歸求解找到經緯度所對應的三角格子,坐標轉換相對容易;而GoodChild等(1992)以及Otoo等(1993)基於一定的數學假設推導出QTM擴展投影方程,將經緯度坐標快速轉換到平面上,坐標計算簡單快速。LianSong所設計的模型通過調整小圓弧空間關係構建等面積三角剖分,計算方式複雜,坐標轉換困難,計算量大。第3種剖分方式直接剖分投影三角面,單點坐標轉換方便,但剖分幾何意義不明確,有的能保證等面積特性,但等角變異大,如基於Snyder等面積投影的ISEA剖分模型邊界扭曲嚴重,投影計算複雜,投影和逆投影轉換沒有顯式求解方法;有的能保證等角形變,如Gnomonic投影(即SQT剖分模型),但面積變異太大;Fuller-Gray投影能保證等角和等面積特性相對均衡,但坐標計算較複雜(投影坐標反算到經緯度坐標無顯式解,需要通過數字逼近方法計算得到)。Goodchild,White和Clarke等(1995)分別對全球網格剖分模型的設計和選擇標準進行了研究,指出全球網格模型評價和設計原則是一個多要素相互獨立的多指標體系,已知剖分模型中不存在一種所有評價指標最好的模型,每個模型或者一些指標性能很好,但另外一些指標相對較差。
根據空間信息表達、組織和管理的應用特點,本文選擇剖分等形狀、等面積、坐標轉換計算簡單快速作為全球格網主要評價指標。按該三指標體系,已有的剖分模型的指標性能不均衡,如Fuller-Gray和ISEA剖分相對等形狀和等面積,但坐標轉換繁瑣,而且ISEA邊界扭曲嚴重;QTM坐標轉換相對容易,但形狀和面積的分佈存在較大差異。本文設計了等角比例投影,該投影可支持包括正八面體,正二十面體等多種柏拉圖立體,球面特徵曲線(緯度圈,大圓弧等)上的均勻剖分點均勻地投影到投影面中。該投影的數學幾何模型簡單,逆計算方便。按照該投
影性質,然後基於正二十面體構建了EARPIH剖分模型。該模型幾何意義明確,較好地滿足了近似規則、等邊、等面積的要求;剖分邊界相對平滑,扭曲不明顯;同時球面點與格網的關係轉換為投影與投影三角格網間的線性關係。與其他剖分模型相比,三指標相對均衡,是一種比較理想的剖分模型。
全球格網中只有原始球面三角能夠保證嚴格的等形狀特性,比如正八面體的球面剖分或者正二十面體球面剖分,其他任意深度的剖分將破壞等邊性,等面積性。因此只能盡量保證近似等邊性以及近似等面積性。由於全球網格模型構建方法種類繁多,包括球面直接剖分、球面弦剖分以及投影平面剖分等方式,難以直接進行投影方程的面積形變和角度形變分析。因多數剖分的邊界定義模糊,計算複雜,本文將以剖分單元的3個頂點為計算依據,採用類似Dutton的方法直接利用每個球面三角單元對應的平面三角作為標準進行QTM、ISEA、SQT和EARPIH模型的比較,當剖分越深,平面三角的弦邊與球面三角的弧邊越接近,球面三角也越接近平面三角。
在正二十面體等角比例投影基礎上,本文構建了EARPIH正二十面體球面剖分模型。該剖分模型有兩種產生方法:一種是投影平面均分的三角格網反投影到球面產生;第二種方法直接均勻剖分球面特徵弧段,結點的幾何意義明確,但邊界定義模糊,必須藉助第一種方法解決。
全球網格模型的空間幾何均勻性直接與正多面體的階數相關,階數越大,剖分越相對均勻,如基於正八面體的QTM與基於正二十面體的EARPIH,ISEA,SQT等模型相比,等面積性和等邊性存在較大差異,性能相對較差。而後3種剖分基於正二十面體,階數最高,有關指標相對接近。與ISEA相比,EARPIH的主要優勢在於計算相對簡單,投影方程和逆投影方程具有顯式解,而ISEA計算複雜,投影和逆投影轉換隻能通過數字計算方式,且ISEA的剖分邊界存在嚴重的扭曲。EARPIH的等面積性好於SQT。總之,以等邊性比較,SQT最好,EARPIH好於ISEA,QTM最差;在等面積性方面,ISEA最好,EARPIH次之,SQT第三,QTM最差;計算方法方面,QTM最簡單,SQT與EARPIH涉及三角函數,計算複雜度接近,而ISEA最為複雜。因此EARPIH基本滿足了設計標準,三個指標相對均衡。
