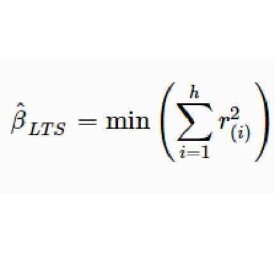穩健回歸

穩健回歸(robust regression)是將穩健估計方法用於回歸模型，以擬合大部分數據存在的結構，同時可識別出潛在可能的離群點、強影響點或與模型假設相偏離的結構。當誤差服從正態分佈時，其估計幾乎和最小二乘估計一樣好，而最小二乘估計條件不滿足時，其結果優於最小二乘估計。

穩健性測度常用影響函數IF(influence function)及其擴展概念和崩潰點BP(breakdown point)。

也稱影響曲線(influence curve)，它表示給出分佈為F的一個(大)樣本，在任意點x

處加入一個額外觀測后對統計量T的(近似或標準化的)影響。如x以的概率來自於既定分佈F，則其來自於另一個任意污染分佈的概率為δ，此時的混合分佈為：

統計量T的影響函數就定義為：

粗略地說，影響函數是統計量T在一個既定分佈F下的一階導數，其中點x是有限維數的概率分佈空間的坐標。如果某個統計量的IF有界，我們就稱此統計量具有極微小穩健性。從IF推導出的還有“過失誤差敏感度”GES(gross error sensitivity)，它作為主要的局部穩健性尺度，可用以度量固定大小的極微小污染對統計量導致的最大偏差，即F的微小擾動下T的穩定性。如果一個穩健統計量的漸近偏差其上界是有限的，即有界，此時稱T滿足B-robust(B表示偏差bias)；另外一個從IF推導出的概念是IF的范數，即T的漸近方差，可作為基本的估計效率尺度。這兩個范數都依賴於F，於是可視之為新的泛函，其微小變化下的穩定性(經恰當的標準化后)可由“偏差改變函數”CBF(change of bias function或change of biascurve)和“方差改變函數”CVF(change of variance function或change of variance curve)和“方差改變函數”CVF(change of variance function或change of variance curve)來度量。這兩個函數的上確界范數又可以作為簡單的總結量，分別稱為“偏差改變敏感度”CBS(change of bias sensitivity)和“方差改變敏感度”CVS(change of variance sensitivity)。如果CVS有界，可稱T滿足V-robust(V表示方差variance)。從概念上講．V-robust要強於B-robust。

崩潰點是一個全局穩健性尺度。其起初的定義由Hodges針對於單變數情況下位置參數的估計提出，後由Hampel將其推廣到更一般情形，回歸分析中相對較為實用的概念是Donoho和Huber所提出的它在有限樣本條件下的表達：

其中Z為自變數與因變數組成的觀測值空間，為回歸估計向量，偏差函數bias表示從Z空間的n個觀測中任意替換任意大小的m個值以後(即考慮最壞情況下的離群數據)，回歸估計 所發生變化的上確界。不太嚴格地講，回歸估計的崩潰點就表示可使估計值 越過所有邊界的過失誤差最小比例。稍準確一點，它是距離模型分佈的一個距離，超過此距離統計量就變得完全不可靠，且其值越小估計值越不穩健。

穩健回歸估計主要包括基於似然估計的M類、基於殘差順序統計最某些線性變換的L類、基於殘差秩次的R類及其廣義估計和一些高崩潰點HBP(high breakdown point)方法。

R估計是Jackel等學者提出一種非參數回歸方法。該方法不將殘差取平方，而是將殘差的秩次的某種函數作為離群點的降權函數引入估計模型，這樣可以減小離群點對估計量的影響，從而達到穩健性要求。

R估計函數如下定義：

其中 為殘差，為殘差的秩次， 為殘差秩次的得分函數。得分函數 ，其中最常用的是Wilcoxon得分函數： 。代入上面定義式，得到此估計的目標函數為：

對其求極小，可得到相應回歸係數的Wilcoxon R估計值。數值計算上其回歸係數可採用梯度法實現，截距可由估計值殘差的中位數得到。經證明此估計量是漸近無偏的，且滿足位置、尺度同變性。

常見的高崩潰點回歸包括最小平方中位數(least median of squares) LMS回歸、 LTS(least trimmed squares) 回歸、 S估計、 GS估計、 MM估計和 估計等。

LMS與LTS估計

考慮到經典LS估計的目標函數定義為使得各殘差的平方和最小也就相當於使各殘差平方的算術均數最小，而算術均數對於偏離正態分佈的情況其估計顯然是不穩健的，但在此情況下中位數卻非常穩健，於是將LS估計的目標函數改為使各殘差平方的中位數最小，得到的“最小平方中位數”估計應該是穩健的，即定義：

類似地，由於在單變數情況下的“調整均數”(trimmed mean)是穩健的，所以考慮在回歸情形下如果把殘差較大的點棄去不計，目標函數是使排序在前一部分較小的殘差平方合計最小，可定義 LTS估計如下：

式中的 由各殘差從小到大排序后得到，即 。可以注意到該估計方法的崩潰點大小與h值的設定有關，其值越小，崩潰點越大，一般情況下取為(3n+p+1)/4時可兼顧崩潰點與估計效率。這兩種估計方法剛提出時均採用的是重複抽樣演演算法(resampling algorithm)，之後的討論和改進主要是考慮如何在盡量減少運算量的情況下得到近似或確切的估計值，如基於Chebyshev擬合的對偶型線性規劃演演算法尋找可行解集(feasible set algorithm)等，目前多採用的是改進的快速演演算法。

遺憾的是由於其殘差分佈未知，所以其估計值的標準誤沒有顯解式，此情況下可以考慮使用Bootstrap方法作統計推斷。而多數情況下由於這兩種估計具有較高的崩潰點，它被用來作離群點診斷或得到其他穩健估計方法的初值。例如提出這類方法的Rousseeuw等人建議可以在LTS或LMS估計基礎上進行“再加權最小二乘估計”(reweighted least sum of squares)，即棄去那些殘差較大的點，對剩餘數據進行普通最小二乘估計，或等價地將權重定義為：

進行加權最小二乘估計，其中為根據LTS或LMS估計得到的各點殘差，s為殘差的標準差估計值：

常數k與前述M估計中的1.345一樣，對應於穩健性與估計效率的折中，一般建議取2.5。

S估計

該法也由Rousseeuw和Yohai提出，所謂的S估計，它對回歸係數的選擇使得方程

的解有最小的s，這裡函數 通常選用Tukey的雙平方函數

的積分，另外在前面方程中選擇及，這種選擇主要是為了和正態誤差一致。