軌跡方程

符合一定條件的動點所形成的圖形，或者說，符合一定條件的點的全體所組成的集合，叫做滿足該條件的點的軌跡．

軌跡，包含兩個方面的問題：凡在軌跡上的點都符合給定的條件，這叫做軌跡的純粹性（也叫做必要性）；凡不在軌跡上的點都不符合給定的條件，也就是符合給定條件的點必在軌跡上，這叫做軌跡的完備性（也叫做充分性）．

平面軌跡一般是曲線，空間軌跡一般是曲面。 【例如】A，B是兩個定點，k（>0）是一個常數，滿足MA:MB=k的動點M的軌跡：

在平面上表示一條直線（k=1）或一個圓周（k≠1）；

在空間內表示一條平面（k=1）或一個球面（k≠1）。

【軌跡方程】就是與 幾何軌跡對應的 代數描述。

一、求動點的軌跡方程的基本步驟

⒈建立適當的坐標系，設出動點M的坐標;

⒉寫出點M的集合；

⒊列出方程=0;

⒋化簡方程為最簡形式；

⒌檢驗.

二、求動點的軌跡方程的常用方法：

求軌跡方程的方法有多種，常用的有直譯法、定義法、相關點法、參數法和交軌法等.

⒈直譯法：直接將條件翻譯成等式，整理化簡后即得動點的軌跡方程，這種求軌跡方程的方法通常叫做直譯法.

⒉定義法：如果能夠確定動點的軌跡滿足某種已知曲線的定義，則可利用曲線的定義寫出方程，這種求軌跡方程的方法叫做定義法.

⒊相關點法：用動點Q的坐標x,y表示相關點P的坐標x0、y0，然後代入點P的坐標（x0,y0）所滿足的曲線方程，整理化簡便得到動點Q軌跡方程，這種求軌跡方程的方法叫做相關點法.

⒋參數法：當動點坐標x、y之間的直接關係難以找到時，往往先尋找x、y與某一變數t的關係，得再消去參變數t，得到方程，即為動點的軌跡方程，這種求軌跡方程的方法叫做參數法.

⒌交軌法：將兩動曲線方程中的參數消去，得到不含參數的方程，即為兩動曲線交點的軌跡方程，這種求軌跡方程的方法叫做交軌法.

*直譯法：求動點軌跡方程的一般步驟

①建系——建立適當的坐標系；

②設點——設軌跡上的任一點P（x，y）；

③列式——列出動點p所滿足的關係式；

④代換——依條件的特點，選用距離公式、斜率公式等將其轉化為關於X,Y的方程式，並化簡；

⑤證明——證明所求方程即為符合條件的動點軌跡方程。

典型例題

例1、已知Q點是雙曲線上異於二頂點的一動點，F1、F2是雙曲線的左、右焦點，從F2點向∠F1QF2的平分線作垂線F2P，垂足為P點，求P點的軌跡方程.

分析：注意圖形的幾何性質，聯想到雙曲線的定義，可考慮用定義法求軌跡方程.

解答：如圖，連結OP，則由角平分線的性質，

得|AQ|=|F2Q|.

由三角形中位線性質，得.

.

（若點Q在雙曲線的左支上時，應為）.

即.∴P點軌跡方程即為.

例2、設動圓C的對稱軸平行於坐標軸，長軸長為4，且以y軸為左準線，左頂點A在拋物線y2=x-1上移動，求這些橢圓的中心C的軌跡方程.

分析：A點和C點是一對相關點，設法將A點的坐標用C點坐標表達，用相關點法求C的軌跡方程.

解答：設中心C的坐標（x,y），則A的坐標為（x-2,y），又A在拋物線y2=x-1上移動.

∴y2=(x-2）-1，即y2=x-3，此即所求C的軌跡方程.

另外，問題也可用參數法求解.

∵左頂點A在拋物線y2=x-1上移動，

∴設A(t2+1,t)(t為參數）.

∵y=yA=t，①

∵2a=4，∴a=2，∴x=xA+2=t2+3. ②

由①、②消去參數t，得中心C的軌跡方程是y2=x-3.

例3、如圖，P是拋物線C：上一點，直線l過點P且與拋物線C交於另一點Q.若直線l與過點P的切線垂直，求線段PQ中點M的軌跡方程.

分析：這是2004年全國高考題（福建卷）理科的壓軸題，依題意直線l的方程可用P的橫坐標表達，於是選擇以P的橫坐標為參數，用參數法求解動點M的軌跡方程.

解答：設P(x1,y1），M(x0,y0），其中x1≠0.

由，①

由，∴過點P的切線的斜率k切=x1,

∴直線l的斜率，

直線l的方程為 ②

聯立①②消去y，得.

∵M為PQ的中點，∴

消去x1，得.

∴PQ中點M的軌跡方程為.

另外，此題屬"中點弦"的問題，可考慮用"點差法"來處理。探求x0與x1的關係.

設P2(x2,y2），於是由.

得，

則，

將上式代入②並整理，得.

∴PQ中點M的軌跡方程為.

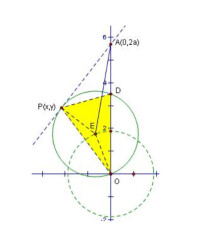
例4、已知常數a>0，在矩形ABCD中，AB=4,BC=4a,O為AB的中點，點E、F、G分別在BC、CD、DA上移動，且，P為GE與OF的交點（如圖）.問是否存在兩個定點，使P到這兩點的距離的和為定值？若存在，求出這兩點的坐標及此定值；若不存在，請說明理由.

分析：這是一道探索性問題，首先求出P點坐標滿足的方程，再根據此判斷是否存在兩定點，使P到兩定點的距離之和為定值。鑒於P為兩直線GE和OF的交點，可用交軌法求解P的軌跡方程.

解答：以O為原點，AB所在直線為x軸建立如圖的直線坐標系.

按題意有A(-2,0),B（2,0),C（2,4a),D(-2,4a).

設（0≤k≤1），

由此有E（2,4ak),F（2-4k,4a),G(-2,4a-4ak).

直線OF的方程為：2ax+（2k-1）y=0，①

直線GE的方程為：-a（2k-1）x+y-2a=0，②

從①，②消去參數k，得點P(x,y）坐標滿足方程2a2x2+y2-2ay=0,

整理得.

當時，點P的軌跡為圓弧，所以不存在符合題意的兩點.

當時，點P的軌跡為橢圓的一部分，點P到該橢圓焦點的距離和為定長.

當時，點P到橢圓兩個焦點的距離之和為定值.

當時，點P到橢圓兩個焦點的距離之和為定值2a.

例5、動直線l過定點A（2,0），且與拋物線y=x2+2相交於不同的兩點B和C，點B和C在x軸上的射影分別是B′和C′（如圖），P是線段BC上的點，並滿足關係式|BP|∶|PC|=|BB′|∶|CC′|，求POA的重心G的軌跡方程.

分析：本題是一道較複雜的軌跡綜合題，動點G的位置取決於P點的位置，即P是G的相關點，又P在動直線l上，l繞定點A（2,0）而動，依前所述，選用斜率k為參數較合理，又相應點P在運動時，還要滿足這一比值，這又出現了另一參數λ，為多元參數.

解答：設直線l的斜率為k，顯然l與x軸垂直時，l與拋物線不可能有兩個交點，故l的方程為y=k(x-2） .將它與拋物線方程聯立，消去y得x2-kx+2+2k=0.

此方程有兩個不同實根的充要條件是=k2-4（2+2k)=k2-8k-8=0.

解得，或. ①

設B、C兩點的坐標為（x1,y1），（x2,y2），則x1+x2=k,x1x2=2+2k. ②

令③設，依定比分點公式，有④設動點G的坐標為（x,y），則將④、③、②分別代入上式並注意到，

可得 消去k得12x―3y―4=0.

另外，由可得，代入①，得，或.

解之得（並注意到y≠4）.，若.

因此，POA的重心G的軌跡方程為12x-3y-4=0.

其中.

它表示一條除去端點及其點的線段.

點評：解決本題時，應充分注意所求軌跡方程中y的取值範圍，這是最容易出現失誤的，甚至可能發生根本不去求出k的範圍，而誤認為所求的軌跡方程為12x-3y-4=0.

例6、如圖所示，給出定點A(a,0）和直線l:x=-1,B是直線l上的動點，∠BOA的角平分線交AB於點C，求點C的軌跡方程，並討論方程表示的曲線類型與a值的關係.

分析一：藉助交軌法和參數法，並利用角平分線上一點到角的兩邊的距離相等的性質解題.

解答一：依題意，記B(-1,b),(b∈R），則直線OA和OB的方程分別為y=0或y=-bx，設點C(x,y），則有0≤x據點到直線的距離公式可得. ①

由於點C在直線AB上，故有.

由x-a≠0，得. ②

將②代入①得.

整理，得，

若y≠0，則（1-a)x2-2ax+（1+a)y2=0(0若y=0，則b=0，∠AOB=π，點C的坐標為（0,0），滿足上式.

綜上得點C的軌跡方程為（1-a)x2-2ax+（1+a)y2=0(0≤x⑴當a=1時，軌跡方程化為y2=x(0≤x<1），此時，方程表示拋物線弧段.

⑵當a≠1時，軌跡方程化為.

所以，當0當a>1時，方程表示雙曲線一支的弧段.

分析二：藉助兩倍角的正切公式解題.

解答二：如圖所示，設D是l與x軸的交點，過點C作CE⊥x,E是垂足.

⑴當|BD|≠0時，設點C(x,y），則0由CE//BD，得.

∵∠COA=∠COB=∠COD-∠BOD=π-∠COA-∠BOD，又2∠COA=π-∠BOD.

∴.

整理，得.

⑵當|BD|=0時，∠BOA=，則點C的坐標為（0,0），滿足上式.

綜合⑴、⑵，得點C的軌跡方程為（1-a)x2-2ax+（1+a)y2=0(0以下同解法一.

分析三：由於C、A、B三點在一直線上，而A、B在特殊直線上，故可構造定比分點公式模型解決本題.

解答三：設C(x,y），其中0≤x∵OC平分∠AOB，∴，從而，

由定比分點公式 即

分別用b2、代入有，

化簡得.

以下同解法一.

點評：對於本題給出的三種解法，實質上是分別從三種不同的角度去審視問題的結果。這同時也表明，即使是一個較難的問題，只要我們深入地挖掘問題的各種知識背景，就完全有可能找出一個個異彩紛呈的解法，從而由此提高綜合分析問題與解決問題的能力以及增強解題的創新意識.

總之，在解決求解軌跡方程問題時，要重視基該方法的綜合運用，要有意識地去觀察圖形的幾何性質，要合理地去選擇參數，還應特別留意軌跡的完備性和純粹性.

鞏固練習

⒈一動圓與兩圓x2+y2=1和x2+y2-8x+12=0都外切，則動圓圓心軌跡是()

A.圓B.橢圓 C.雙曲線的一支 D.拋物線

⒉已知點P在直線x=2上移動，直線l通過原點且與OP垂直，通過點A（1,0）及點P的直線m和直線l交於Q，求點Q的軌跡方程.

⒊如圖，設點A和B為拋物線y=4px(p>0）上原點以外的兩個動點，已知OA⊥OB,OM⊥AB.求點M的軌跡方程.

⒋已知橢圓直線l:.P是l上一點。射線OP交橢圓於點R，又點Q在OP上且滿足|OQ|·|OP|=|OR|2，當點P在l上移動時，求點Q的軌跡方程，並說明軌跡是什麼曲線.

參考答案：

⒈C

⒉

⒊x2+y2-4px=0(x≠0)

⒋點Q的軌跡方程為（其中x,y不同時為零），其軌跡是以（1,1）為中心，長短半軸分別為和且長軸與x軸平行的橢圓，去掉坐標原點.

數學應用題的解題方法

應用問題是考查應用數學意識和能力的極好題型，它題材貼近生活，涉及知識面廣，題型功能豐富，增加應用性與能力性試題是高考改革的方向，解決實際問題的應用題已成為高考的熱點.

解答應用問題就是在閱讀材料，理解題意的基礎上，把實際問題抽象轉化成數學問題，建立相應的數學模型，再利用數學知識對數學模型進行分析、研究，得到數學答案，然後再把數學答案返回到實際問題中去，獲取具有實際意義的結論，求解數學應用問題的思路和方法，可以用示意圖表示為：

下面就應用題常見的數學模型舉一些實例，以求開闊同學們的思維，受到一些啟示.

⒈建立函數模型

例1、某小區欲建一面積為a平方米的矩形綠地，四周有小路，綠地長邊外小路寬為5米，短邊外小路8米（如圖）.綠地長邊至多長28米，至少長20米。對於給定的a（300≤a≤700），怎樣設計綠地的長寬使綠地和小路總佔地面積最小?

分析：引入長邊長為自變數x，建立關於總佔地面積的目標函數x，再利用函數性質和不等式知識求解.

解答：設綠地的長邊為x米（x>0），則短邊為米，且。總佔地為S平方米.

當且僅當，即時，上式中等號成立，滿足等號成立的充要條件為：

即250≤a≤490.又依條件300≤a≤700.

故⑴當300≤a≤490，即時,S有最小值，此時長為，寬為米.

⑵當490≤a≤700時，設.

.

這是因為20≤x≤28,a>490，使得28-x≥0,16a>7840≥280x的緣故.

因此，當x=28時，S有最小值，並注意到此時.

點評：求解函數模型經常要用到不等式的知識，有兩點特別值得注意，一是函數自變數範圍應在實際意義下考慮；二是在利用均值不等式求函數最值時，必須要檢驗等號是否能夠成立.

例2、制定投資計劃時，不僅考慮可能獲得的盈利，而且要考慮可能出現的虧損.

某投資人打算投資甲、乙兩個項目。根據預測，甲、乙項目可能的最大盈利率分別為100%和50%，可能的最大虧損率分別為30%和10%.投資人計劃投資金額不超過10萬元，要求確保可能的資金虧損不超過1.8萬元。問投資人對甲、乙兩個項目各投資多少萬元，才能使可能的盈利最大?

分析：這是今年江蘇高考試題，可將總盈利z表達成甲、乙兩個項目的投資額x、y的目標函數z(x、y），問題就轉化為在x、y約束條件（不等關係）的最值問題，可藉助線性規劃知識求解.

解答：設投資人分別用x萬元、y萬元投資甲、乙兩個項目，

由題意知，

目標函數z=x+0.5y.

上述不等式組表示的平面區域如圖所示，陰影部分（含邊界）即可行域.

作直線l0:x+0.5y=0，並作平行於直線l0的直線x+0.5y=z(z∈R），與可行域相交，其中有一條直線經過可行域上的M點，且與直線x+0.5y=0的距離最大。這裡M點是直線x+y=10和0.3x+0.1y=1.8交點.

解方程組，得x=4,y=6.

此時z=4+0.5*6=7（萬元）.∴當x=4,y=6時，z取得最大值.

答：投資人用4萬元投資甲項目，6萬元投資乙項目，才能在確保虧損不超過1.8萬元的前提下，使可能的盈利最大.

點評：這是一道線性規劃問題，是運籌學中最基礎的內容，可用中學知識求解。一般採用的方法有目標函數分析法和圖解法。學生在解決這類問題時的主要困難之處在於不會把約束條件中的多個等式或不等式與所求目標溝通起來，關於簡單線性規劃問題，高中數學新教材中已增加了此項內容，我們在複習過程中應給予一定的重視.

⒉建立數列模型

例3、某城市2001年末汽車保有量為30萬輛，預計此後每年報廢上一年末汽車保有量的6%，並且每年新增汽車數量相同，為保護城市環境，要求該城市汽車保有量不超過60萬輛，那麼每年新增汽車數量不應超過多少輛?

分析：引入新增汽車數量為未知數，以各年末的汽車保有量為項建立數列模型，藉助數列知識求解.

解答：2001年末汽車保有量為b1萬輛，以後各年末汽車保有量依次為b2萬輛，b3萬輛，…，每年新增汽車x萬輛，則：

b1=30,b2=b1*0.94+x.

對於n>1，有bn+1=bn*0.94+x=bn-1*0.94x2+（1+0.94）x,

……

當，即x≤1.8時，bn+1≤bn≤…≤b1=30.

當，即x>1.8時，.

並且數列{bn}逐項增加，可以任意靠近.

因此，如果要求汽車保有量不超過60萬輛，即bn≤60(n=1,2,3，…）.

則，即x≤3.6（萬輛）.

綜上，每年新增汽車不應超過3.6萬輛.

評註：求數列的通項是解決問題的關鍵，對於遞推式bn+1=bn*0.94+x，也可作如下化歸處理：

另外還應有一點極限知識才行.

例4、為了保護三峽庫區的生態環境，凡是坡度在25°以上的坡荒地都要綠化造林，經初步統計，在三峽庫區坡度大於25°的坡荒地面積約有2640萬畝，若從2003年初開始綠化造林，第一年造林120萬畝，以後每年比前一年多綠化60萬畝.

⑴若所有被綠化造林的坡荒地全部綠化成功，問到哪一年底可使庫區的坡荒地全部綠化?

⑵若每萬畝綠化造林所植樹苗的木材量平均為0.1萬立方米，每年樹木木材量的自然增長率為20%，那麼當整個庫區25°以上荒地全部綠化完的那一年底，一共有木材多少萬立方米?（保留1位小數，1.29=5.16,1.28=4.30）

分析：每年綠化面積成一等差數列，某年的造林量所形成的以後各年的木材量成一等比數列.

解答：⑴設a1=120,d=60，第n年後可以使綠化任務完成。則有

.

解得n≥8.故到2010年，可以使庫區為25°以上的坡地全部綠化.

⑵∵2010年初造林數量為：a8=120+7*60=540（萬畝）,

設到2010年木材總量為S，依題意有：

令⑴

兩邊乘以1.2得⑵

⑵-⑴得，∴S=6*90.6=543.6（萬立方米）

答：到2010年底共有木材543.6萬立方米.

點評：解決與數列有關的應用問題，要仔細弄清題意，搞清是等差數列還是等比數列的問題，是求某一項還是求和的問題以及項數是多少等等，然後根據有關結論進行計算證明.

⒊建立幾何模型

例5、A、B、C是我方三個炮兵陣地，A在B的正東，相距6km,C在B的北偏西30°方向上，相距4km,P為敵炮陣地。某時刻A地發現敵炮陣地的某種信號，由於B、C兩地比A地距離P較遠，因此4秒鐘后，B、C才同時發現這一信號（已知該信號的傳播速度為每秒1km),A若炮擊P地，求炮擊的方位角.

分析：問題的關鍵是要確定P點的位置，注意到P點滿足的條件|PB|-|PA|=4，且|PB|=|PC|，聯想到雙曲線的定義和中垂線的性質，可通過建立坐標系，用解析幾何模型求解.

解答：如圖，以線段AB的中點為原點，BA所在的直線為x軸建立直角坐標系，則A（3,0),B(-3,0),C(-5,).

∵|PB|-|PA|=4，∴點P在以A、B為焦點的雙曲線的右支上.

該雙曲線右支的方程是. ①

又|PB|=|PC|，∴點P在線段BC的垂直平分線上，該直線的方程為.②

將②代入①得11x2-56x-256=0，得x=8或（舍），於是可得.

又.

故點P在點A的北偏東30°方向上，即A地炮擊P地的方位角是北偏東30°.

例6、現有一放置乒乓球的圓柱形桶，其內徑為（cm），高為40cm，則該桶內最多可放置多少個直徑為4cm的乒乓球?

分析：要解決本例，需要兩個工作，一是計算桶內一層可放置乒乓球多少個？它應該通過桶的內徑與乒乓球的直徑，及第一層乒乓球在底面上的射影等數據與幾何特性進行計算；二是計算桶內最多可放置多少層球？計算第二個問題的關鍵是如何求出兩層乒乓球球心所在平面之間的距離，應根據從相鄰兩層球的球心提煉出球心所組成的幾何體，將計算轉移到該幾何體中進行.

解答：首先建立如圖1所示的幾何模型，其中⊙O1、⊙O2、⊙O3為三個半徑均為2cm且兩兩外切的圓，這三個圓又都內切於⊙O，顯然O1O2O3是邊長為4cm的正三角形，它的高為，∴，若⊙O2與⊙O相切於P，則.

故圓O的半徑為，∴其直徑為（cm），因此在內徑為cm的桶內層可放置3個直徑為4cm乒乓球.

在桶內放置第二層球時，為了使放置的乒乓球儘可能多，因此在放置第二層球時可以考慮利用第一層乒乓球放置后留下的空檔，故應將第二層的三個球放置的位置相對於第一層的三個乒乓球的位置逆時針（或順時針）旋轉60°.這二層六個乒乓球的球心可以看作是如圖2所示的正六稜柱下底面上的三頂點A1、B1、C1與上底面上的三個頂點A2、B2、C2，並且A2B2=4cm，從而我們可以求出這個正六稜柱的底面邊長和高.

設正六稜柱的底面邊長和高分別為x、h，則A2B22=x2+x2-2x2cos120,

.

又.

這樣我們就求得了二層乒乓球的球心所在平面間的距離，若設這個桶內放置了n層的乒乓球，則n應滿足：.

，

又由於，故（n-1）≤11，∴n≤12.

所以這桶內最多可放置12層乒乓球，每層有3個，故這個桶內最多可放置36個乒乓球.

點評：本例我們建立了兩個幾何換型，關鍵是建立了桶內相鄰兩層球中每一個球的球心及它們在另一層球心所在平面上的射影共12個點組成的一個正六稜柱（如圖2）這一幾何模型.

除了上述列舉的三種常用應用題型外，還有三角型，排列組合型，概率型等其它模型，學習過程中應多思多想，加強歸納總結，善於抓住主幹，合理構建數學模型，不斷提高數學的應用意識和應用能力