譜估計
譜估計
譜估計(spectrum estimation) 對隨機信號序列進行功率譜密度估計演演算法的總稱,屬於頻域中描述隨機信號特性的分析方法之―。
隨機信號是不確定的,不能用清楚的數學式表達,只能根據隨機過程理論,利用統計方法來進行分析。經常利用均值、均方值、相關函數和功率譜密度函數等統計量來描述隨機過程的特徵或隨機信號的特性。實際上,經常遇到的隨機過程多是平穩隨機過程而且是各態歷經的,因而它的樣本函數集平均可以根據某一個樣本函數的時間平均來確定。平穩隨機信號本身雖仍是不確定的,但它的相關函數卻是確定的。在均值為零時,它的相關函數的傅里葉變換或Z變換恰恰可以表示為隨機信號的功率譜密度函數,一般簡稱為功率譜。可見隨機信號的功率譜與自相關函數互為傅里葉變換的關係,這兩個函數分別從頻域和時域來描述隨機信號的基本特性。
在很多應用場合,可以觀測到的數據總是有限的,這就需要利用-些方法,根據有限的實測數據估計出整個信號的功率譜。針對不同的要求,如減小譜估計的偏差,減小對雜訊的靈敏程度,提高譜解析度等,已提出許多不同的譜估計方法。在線性估計方法中,有周期圖估計法、相關法和協方差法;在非線性估計方法中,有最大熵譜估計、AR模型法、MA模型法、ARMA模型法和最大似然法等。線性估計方法大多是有偏的譜估計方法,譜解析度隨數據長度的增加而提高。非線性譜估計方法大多是無偏的譜估計方法,可以獲得高的譜解析度。
1807年,法國人傅里葉提出了著名的傅里葉變換,在信號分析與處理中,成為最常用的分析工具。1930年,N.維納發表論文《廣義諧波分析》,引進了自相關函數和功率譜的定義,並證明這兩個函數互為傅里葉變換,這項工作建立了使用傅里葉變換方法處理隨機過程的理論體系。1958年,布萊克愛和圖基給出了用維納相關法從抽樣數據序列得到功率譜的實現方法。該方法首先從觀測數據估計自相關延遲,然後將 自相關估計值乘以窗函數,最後對加窗延遲估計值作傅里葉變換得到功率譜估計。這種方法簡稱BT法,其性能與窗函數的選擇密切相關。1965年庫利和圖基提出了著名的快速傅里葉變換(FFT)這一極有效的演演算法,使得功率譜估計的周期圖估計成為當前最流行的功率譜估計演演算法。BT法和周期圖法所得到的功率譜估計都是應用了經典的傅里葉分析方法,故稱為學弗譜估計法。這兩種譜估計法亦稱為線性譜估計法。BT法與周期圖法的主要弱點是頻率解析度的限制。因為譜解析度的極限受抽樣數據的長度的限制,數據長度越短,譜解析度越低。為了克服這個缺點,1967年,伯格提出了最大熵譜分析法;1968年,帕曾提出了自回歸(AR)譜估計法。1971年,范登-博斯證明了最大熵譜分析與AR譜估計等效。自此構成了現代譜估計的模型參量法:如自回歸(AR)模型、滑動平均(MA)模型、自回歸滑動平均(ARMA)模型及普羅尼(Prony)復指數模型等。同時,還出現了現代譜估計的非參量法:1969年J.卡彭為分析陣列的頻率一波數譜估計而提出了最大似然譜估計法;1971年洛卡斯將其推廣到時間序列的功率譜估計中。現代譜估計的參量法和非參量法,都是基於非線性運算的,故亦稱為非線性譜估計法。這些非線性譜估計方法都具有解析度高的優點,而且特別適用於短數據序列的譜估計。因此這些方法又稱為高解析度的譜估計方法。20世紀80年代初,現代譜估計方法又形成一些新的分支,主要有應用資訊理論的熵譜估計法、奇異值/特徵值分解處理法譜估計、多譜(高階譜)估計及多維譜估計等。現代譜估計的發展已成為當今一門不可缺少的新學科與新技術。
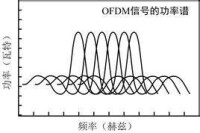
圖 1 OFDM信號的功率譜
在現代譜估計中,對於功率估計的理論、方法的研究已相當深入,應用也比較廣泛。然而功率譜估計僅包含振幅信息,不包含相位信息,大量的實際問題卻常常需要相位信息。另外,對實際觀測到的數據均假定是由正態白雜訊激勵-線性最小相位系統產生的,但實際中有時數據是由非正態白雜訊產生的,而產生數據的系統是線性非最小相位的或非線性的。因此提出多譜(高階譜)問題,多譜定義為高階累積量(與高階矩密切相關的一個量去維傅里葉變換,它含有比功率譜更多的信息。很多領域發現了多譜的應用價值,現在多譜估計已成為現代譜估計發展的新分支。多譜中的雙譜,階數最低,處理方法簡單,含有相位信息,是多譜命長中的“熱點”。一維情況現代譜估計方法所具有的高分辨性能,吸引人們期望二維譜估計亦能存在與其相似性能,這對實際應用是很有意義的。因此二維高解析度譜估計問題與多維陣列譜估計也是當今現代譜估計中發展的新分支。