預拱度
產生的撓度
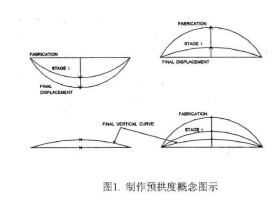
預拱度:為抵消梁、拱、桁架等結構在荷載作用下產生的撓度,而在施工或製造時所預留的與位移方向相反的校正量。確定因素:①腳手架承受施工荷載后引起的彈性變形;②超靜定結構由於混凝土收縮及徐變而引起的撓度;③由於桿件接頭的擠壓和卸落設備的壓縮而產生的塑性變形;④腳手架基礎在受載后的塑彈性沉降;⑤梁、板、拱的底模板的預拱度設置。當結構自重和汽車荷載(不計衝擊力)產生的最大豎向撓度,超過計算跨徑的 1/1600 時,應設預拱度,否則不需要設預拱度。預拱度的設置值為按結構自重和 1/2 可變荷載頻遇值計算的長期撓度值之和採用。根據梁的撓度和支架的變形所計算出來的預拱度之和,為預拱度的最高值,應設置在梁的跨徑中點。其他各點的預拱度,應以中間點為最高點,以梁的兩端為零,按直線或二次拋物線進行分配。
0前言
橋樑撓度的產生的原因有永久作用撓度和可變荷載撓度。永久作用(包括結構自重、橋面鋪裝和附屬設備的重力、預應力、混凝土徐變和收縮作用)是恆久存在的,其產生撓度與持續時間相關,可分為短期撓度和長期撓度。永久作用撓度可以通過施工時預設的反向撓度(又稱預拱度)來加以抵消,使竣工后的橋樑達到理想的線性。
預應力混凝土橋樑的預拱度通常按如下規定設置:當預加應力產生的長期反拱值大於按荷載短期效應組合計算的長期撓度時,可不設預拱度;當預加應力的長期反拱值小於按荷載短期效應組合計算的長期撓度時應設預拱度,其值應按該項荷載的撓度與預應力長期反拱值之差採用。對於位於豎曲線上的橋樑,應視豎曲線的凸起(或凹下)情況,適當增(或減)預拱度值,使竣工后的線性與豎曲線接近一致。可變荷載撓度雖然是臨時出現的,但是隨著可變荷載的移動,撓度大小逐漸變化,在最不利的荷載位置下,撓度達到最大值,一旦汽車駛離橋面,撓度就告消失。因此在橋樑設計中需要驗算可變荷載撓度來體現結構的剛度特性。
1預拱度計算
1.1 構件的預拱度
預應力受彎構件的撓度由兩部分疊加而成:一部分是由外荷載(永久荷載和施工荷載)產生的撓度f,另一部分是預應力產生的反拱f,兩者的差值就是本文定義的受彎構件的撓度f,即f=f-f。為了保證在外荷載和預應力作用下,梁體既不上彎也不下凹,就必須在梁體預製過程中設一個預拱度,其值與撓度 f 大小相等,但方向相反。
1.2 預拱度計算
(1)計算模型。以 35 m 中跨 T 梁梁體在預製、吊運、存放階段的拱度變化作為研究對象,梁體承受預應力和自重作用。假定梁體為等截面,梁的已知條件如下:梁體全截面共配鋼鉸線 30 束,分 3 個孔道,上中下 3 個孔道鋼鉸線的束數分加為9、9、12,鋼鉸線直徑Φ=15.24 mm,公稱截面積140 mm,彈性模量E=1.95×10Pa,標準強度f=1 860 MPa,控制應力δ=0.75f=1 395 MPa,混凝土強度等級為 C50,彈性模量 E=3.45×10Pa,張拉時混凝土的立方體抗壓強度標準值f=40 MPa,梁體自重q=20.7 kN/m,計算跨度l=34.22 m。
(2)截面幾何特徵。經計算,跨中截面幾何特性如下:鋼鉸線重心至截面下邊緣的距離 y1=0.21m;換算截面重心至截面下邊緣的距離 y0=1.256 m;換算截面慣性矩 I =0.494 27 m4 ;凈截面重心至截面下邊緣的距離 yn=1.296 m;凈截面慣性矩 In=0.463 33 m。
(3)由自重產生的撓度 f1。跨中截面撓度 f1 可按一般材料力學的公式計算,即:f1=5/48×Ml2/B0 (1)式(1)中:M—梁重作用下的跨中彎矩;B0—全截面的抗彎剛度,B0=0.95EcI0,0.95 為剛度折減係數。將有關數值代入,求得 f1=3.07 cm。
(4)由預應力產生的反拱 f2。梁體施加預應力后,預應力在梁體中產生偏心預壓力,梁體產生反拱 f2。在本例中,梁體內鋼束的布置為兩段直線夾一段半徑為 5 000 m 的圓曲線。
2 預拱度的設置及效果
2.1 預製梁台座頂面處置
設置預拱度的方法,是將預製梁台座頂面作成下凹曲面。如果曲線設置得當,則梁體在自重和預應力作用下經過一段時間的變形,梁體將既不上拱也不下凹。考慮到每個台座的循環次數較多,施加預應力後台座兩端受力下壓,有部分變形不易恢復,故採取在施工中將台座中央下凹 5.40 cm,下撓曲線形式為二次拋物線,拋物線方程為 y=0.017 5x2-5.40(式中 x 單位為 m,y 單位為 cm)。
2.2 預拱度觀測
由於設計的梁型較多,而實際施工中各種梁型都是按一種預拱度進行控制的,為了使觀測結果更具有代表性,我們選取了跨徑和截面型式相同的 2 片鐵路橋樑、4 片公路橋樑共 6 片梁進行觀測。觀測時間分別為存梁的第 1、第 10、第 30、第 60、第 90、第 120、第 180 天共 7 個時間點進行觀測,
2.3 數據分析
2.3.1 觀測數據的特點
可以看出,梁體撓度值的變化有以下特點:
(1)經過 80 d 的存梁期后,梁體的撓曲變形仍未停止,部分變形將在使用階段完成。
(3)鐵路橋樑的上撓值的變化要比同條件下公路橋樑的上撓值要大。一般情況下,在梁體施加完預應力后,鐵路橋樑的上撓值要減少 2.5 cm 左右,而公路橋樑的上撓值要減少 1.5 cm 左右,在經過相同的存梁期后,鐵路橋樑的剩餘上撓值要小於跨公路橋樑。
(4)同為鐵路橋樑或同為公路橋樑,施加完預應力後梁體的預拱度值經過相同存梁時間后剩餘的預拱度值亦不相同。
2.3.2 原因分析
(1)梁體預拱度變化除與梁體自重、施加預應力大小有關外,還與混凝土的收縮徐變有關,而後者又與張拉時梁體的混凝土強度、養護和載入齡期以及使用過程中外部環境條件等有關。施加預應力大小是跨鐵路梁與跨公路梁預拱度變化相差較大的主要原因,因為這兩種梁自重相差很小,但鋼絞線的配置卻相差較大,跨鐵路梁要比跨公路梁多配置 3~5 根鋼絞線,控制張拉力相差 585.9~976.5 kN。
(2)不同的台座或同一台座預製不同的梁時,其下撓曲線與設計的並不完全相同,這是造成同一種梁型,施加相同的預應力后,經過相同的時間剩餘的預拱度各不相同的主要原因。在今後的施工中,應針對不同的梁型設置不同的預拱度值,使預拱度的設置進一步趨於合理。
1 前言
預應力混凝土連續梁橋具有跨越能力好、受力性能好、變形小、伸縮縫少、行車平順舒適、抗震能力強等優點而受到青睞.預應力混凝土連續梁橋施工採用懸臂澆築工藝,雖然方便了施工,但是在橋樑的整個施工過程中,其結構體系一直處於變化狀態,結構的應力和位移也隨之變化.為了保證橋樑的施工質量和施工安全,橋樑施工控制是必不可少的.上海城建學院的李國平等 針對大跨度連續剛構橋和連續梁橋施工控制提出線形最優施工控制的方法和理論,該理論將成橋線形和施工階段結構變位狀態作為線性、離散、確定性動態結構系統的最優控制對象,根據連續梁橋懸臂澆築的特點,控制目標函數、約束條件、狀態與變數以及具體實施方法等,並在上海吳淞大橋和富春江大橋的施工中得到實際應用.對於大跨徑預應力混凝土連續梁橋,在多種因素的影響下橋樑的施工會伴隨一定的下撓,具體包括梁段自重、預加力張拉與損失、掛藍 ( 支架) 行走、彈性模量、日照和溫度影響、混凝土收縮與徐變及二期恆載. 因此在連續梁橋的施工過程中各個梁段的實際位置會發生與預期位置偏離的現象,使連續梁橋永久線型與設計線型不一.為了保證橋樑結構的線形美觀,準確預致測連續梁橋的預拱度在橋樑的建設過程中至關重要. 灰色系統理論於 20 世紀 80 年代提出,90 年代初開始應用於連續梁橋的施工監控,是一種被筆者以瀋陽四環廣泛認可的橋樑監控理論在建的西蘇堡特大橋為例,利用灰色系統理論合理預測橋樑預拱度,結合現場的監控數據,研究實際工程中大跨徑預應力混凝土連續梁橋的線型控制方法,結果表明採用灰色系統理論 GM ( 1,1) 模型可以準確地對連續梁橋預拱度進行預測,該方法是一種合理的連續梁橋預拱度預測方法.
2預測模型工程實踐應用
工程概況
西蘇堡特大橋主橋全長為360 m,上部結構採用預應力混凝土變截面連續箱梁,跨徑組合為70m + 2 × 110 m + 70 m,橋樑總寬度為39 m,採用雙幅分離式斷面形式,單箱單室連續箱梁,每幅寬度為16. 5 m.箱梁採用掛籃對稱懸臂澆築施工方法,0 號塊托架現澆長度為12 m,兩側各有14 個懸澆梁段.單幅有4 個合攏段,即兩個邊跨合攏段和兩個中跨合攏段.
根據實際情況,採用MIDAS 有限元分析軟體模擬橋樑的施工過程,建立空間桿系梁單元計算模型,全橋共94 個單元,每個節段的施工過程模擬為一個階段模型,每個節段的施工過程包括移動掛藍、混凝土澆築、張拉預應力三個工況,邊界條件採用與施工過程一致.
3成橋控制結果
預拱度設置是為了防止在施工過程中產生的撓度影響橋樑合攏乃至橋樑的最終線形,理論計算的依據也是橋樑各個施工階段產生的撓度,因此,可以通過對梁段撓度的分析體現橋樑預拱度的設置是否合理.目前,該連續梁橋已經完成14 號梁段的澆築,筆者以5 號墩箱梁小里程樁號方向施工控制結果為例,來說明灰色系統理論應用於連續梁橋施工監控的優越性 .
從圖2 中可以看出,數值和曲線均沒有明顯的突變.採用灰色系統理論之後由於調整了橋樑的立模標高,合攏之後橋樑的實測標高值與設計標高值變化趨勢吻合,保證橋樑線型符合設計線型.根據實測數據,採用灰色系統理論后合攏段懸臂端對應控制點最大高差為15 mm,在20 mm 之內,為橋樑的順利合攏提供保障,達到了施工監控的預期目的.
4 結論
預應力連續箱梁橋懸臂施工是一個非平穩的隨機過程,可以看成是一個灰色過程.筆者以西蘇堡特大橋為例,應用灰色系統理論GM (1,1)模型,預測連續梁橋施工過程中的預拱度,由相關公式推導得到11 號梁段的預拱度與實際值相對誤差為4. 02% ,其他梁段的預測相對誤差均不超過8% ,預測結果滿足精度要求,橋樑合攏前,即最大懸臂端澆築完成,對應懸臂端控制點的最大高差為15 mm,能夠保證橋樑的順利合攏.因此,灰色系統理論可以對連續梁橋施工過程中的位移狀態進行有效的控制,保證橋樑線形符合設計要求,具有廣泛的實際應用價值.