共找到3條詞條名為斜面的結果 展開
- 克服垂直提升重物之困難的機械
- 1962年周彥、陳冀聯合執導科教片
- [墨] 阿爾豐索·雷耶斯所著書籍
斜面
克服垂直提升重物之困難的機械
斜面是一種簡單機械,可用於克服垂直提升重物之困難,省力但是費距離。距離比和力比都取決於傾角:斜面與平面的傾角越小,斜面較長,則省力越大,但費距離。
斜面是古希臘人提出的六種簡單機械之中的一種。亞歷山大的帕普斯(290年-350年)在著作《數學彙編》(《Mathematical Collection》),第八卷里嘗試解析斜面的重物平衡問題。他似乎是古希臘唯一做這類研究的幾何學者。雖然他的方法並不正確,但給予後來的學者極大的啟發。歐洲物理學者尼摩的約但努斯傳授的一位無名氏學生於十三世紀撰寫了著作《約但努斯論述重量理論之書》(《Jordanus's Book on the Theory of Weight》)。這本書後來印版發行於1565年。在這本書里,應用約但努斯原創的“位形重力”(positional gravity,gravitas secundum situm)概念,首先給出了正確解答。1608年,西蒙·斯特芬發表著作《數學紀要》(《Mathematical Collection》),對於這問題給出正確與精彩的解析,稍後會有更詳細敘述。伽利略·伽利萊也花了很多時間,找出問題錯誤所在,並且用不同方法給出正確答案。
斜面與平面的傾角越大,斜面較短,則省力越小,但省距離。斜面在生活中有廣泛的應用,如盤山公路、搬運滾筒、斜面傳送帶等。在不計算任何阻力時,斜面的機械效率為100%,如果摩擦力很小,則可達到很高的效率。即用F2表示力,s表示斜面長,h表示斜面高,物重為G。不計無用阻力時,根據功的原理,可得:F2s=Gh。
斜面(inclined plane)是一種傾斜的平板,能夠將物體以相對較小的力從低處提升至高處,但提升這物體的路徑長度也會增加。斜面是古代希臘人提出的六種簡單機械之中的一種。假若斜面的斜率越小,即斜面與水平面之間的夾角越小,則需施加於物體的作用力會越小,但移動距離也越長;反之亦然。假設移動負載不會造成能量的儲存或耗散,則斜面的機械利益是其長度與提升高度的比率。
在日常生活中,時常會使用到斜面。行駛車輛的坡道是一種常見的斜面;卡車裝載大型貨物時,常會在車尾斜搭一塊木板,將貨物從木板上往上推,所應用的也是斜面的理論。
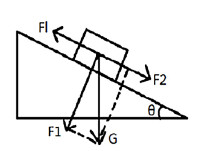
物體靜止在斜面上受到這些力:物體自身的重力(G),斜面對之的支持力(F支),對物體的摩擦力(f靜)等。已知斜面的傾角和物體的重力時,我們可以求出另外的兩個力:
斜面
斜面
斜面
斜面
斜面
斜面
斜面
從山頂到山腳的傾斜面叫斜面,也叫斜坡或山坡。在地圖上明確斜面的具體形狀,對定向越野有一定價值。斜面按其形狀可分為:實地坡度基本一致的斜面叫等齊斜面,全部斜面均可通視。地圖上,從山頂到山腳,間隔基本相等的一組等高線,表示為等齊斜面。
凸形斜面
實地坡度為上緩下陡的斜面叫凸形斜面,部分地段不能通視。地圖上,從山頂到山腳,間隔為上面稀、下面密的一組等高線,表示為凸形斜面。

斜面
波狀斜面
實地坡度交叉變換、陡緩不一、成波狀形的不規則斜面叫波狀斜面,若干地段不能通視。地圖上,表示該狀斜面的等高線間隔稀密不均,沒有規律。
對於一般斜面來說,如果不計算任何的阻力,根據功的原理,斜面的 機械效率是100%,但是不可避免存在一些阻力,如摩擦力和空氣阻力。下面我們就著摩擦力來計算機械效率。我們用θ表示斜面的傾角,G表示物重,Fl表示拉力,fm表示摩擦力,μ表示斜面摩擦力係數,s表示斜面長,h表示斜面高,Wy表示有用功,Wz表示總功,We表示額外功,而F2是順著斜面向下的分力,這些都在“受力情況”一節有提到。
機械效率是100%,但是不可避免存在一些阻力,如摩擦力和空氣阻力。下面我們就著摩擦力來計算機械效率。我們用θ表示斜面的傾角,G表示物重,Fl表示拉力,fm表示摩擦力,μ表示斜面摩擦力係數,s表示斜面長,h表示斜面高,Wy表示有用功,Wz表示總功,We表示額外功,而F2是順著斜面向下的分力,這些都在“受力情況”一節有提到。

斜面
則它的機械效率為:
斜面
斜面
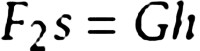
斜面
斜面
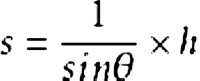
斜面
斜面
即為已知斜面傾角和摩擦係數時的機械效率公式。
使用可移動式斜板,可以輕易地將貨物裝上或卸下密斗貨車。滑梯是兒童遊樂場常見的設施。靠著用滑梯堅硬表面的法向力抵抗重力,工業滑梯可以將易損壞物體(包括人體在內)安全快速地從高處滑下至低處。民用飛機的充氣逃生滑梯能夠允許乘客從飛機出口緊急撤離滑下至地面。
楔子是兩個背靠背的斜面組成的簡單機械。楔子可以用來將物件分開,其操作原理主要是將作用於楔子向下的力轉變為對物件水平的力,而這兩個力幾乎垂直。常見應用楔子原理的工具包括斧頭。
單擺是由一條繩子與一個擺錘組成的實驗儀器,其擺錘的運動軌跡是一個對稱朝上的圓弧。這圓弧可以分割為很多小圓弧,每兩個相鄰的小圓弧最多只相交於一個端點。連接每個小圓弧的兩個端點之間的線段稱為弦。每個弦都可以視為斜面。令增加分割的數量至無限多,每一個小圓弧的弧長趨向為無窮小的極限,所得到無限多小圓弧的對應斜面會組成原本的圓弧。所以,在任意時間,單擺的擺錘可以想像為移動於某特定斜率的斜面。
