排隊網路

排隊網路是指多個排隊系統互相聯接所組成的網路，其中任何一個排隊系統所服務完的顧客可加入其他的排隊系統繼續接受服務，或者離開整個排隊網路。排隊網路與排隊系統的本質區別在於：在排隊網路中，一個顧客一般要在多個服務台處接受服務；而在排隊系統中，一個顧客只在一個服務台處接受服務。在一些嚴格的條件下，排隊網路與排隊系統在理論上沒有太大的區別；但在計算方面，排隊網路中求解一些問題的計算量非常大。

一個排隊網路是由多個服務機構組成的系統。排隊網路中的顧客根據一定的路由機制在服務台之間轉移或離開網路。顧客可能屬於不同的類型，這意味著他們可能有不同的路由機制，不同的服務時間分佈，或不同的服務優先順序。排隊網路可以分為以下三種類型：開放網路，閉網路或混合網路。在一個開放網路中，顧客從網路外部到達該網路並最終離開該網路；在一個閉網路中，顧客在不同服務機構之間轉移而沒有顧客的到達或離開；一個混合網路對某些類型的顧客是開放的，而對其他類型的顧客是封閉的.

排隊網路是一個比較複雜的服務系統，在此系統中經常需要討論多個 隊列的互聯問題，如顧客流的分開與合併，隊列的串、並聯組合等.

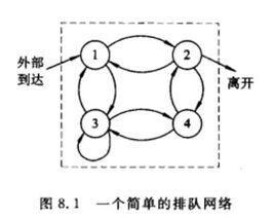
圖8. 1 就描繪了這樣一個簡單的排隊網路，在此排隊網路中包含了四個節點，每個節點代表一個服務站（Service center)(例如計算機系統中的處理單元 (CPU或I/O設備）或者是通信系統中的某些網路節點（交換機或路由器）），每個服務站中包括一個隊列（該隊列中可以有一個或多個服務員）。其中互聯的線條表示顧客流。

Q-GERT網路通過採用豐富的節點形式，描述網路中的排隊問題，能表示各種定量和定性信息。具體做法：在GERT網路的基礎上，將節點劃分為若干部分，在各部標註一定的內容，如節點的存儲和排隊特徵、容量及實現節點所需的流等。節點類型和工序表示法如圖1所示。

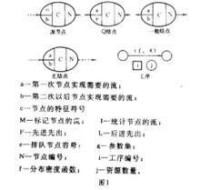
圖1中，Q節點為排隊節點，當容量e為有限時，可能出現：（1）被斥現象，即排隊流量超過了允許容量，新參加排隊的流受到排斥。被系統永久拒絕再進入排隊稱永久排斥；被暫時轉移到其他緩衝節點等待機會再進入排隊稱為暫時排斥；（2）受阻現象，當排隊節點發生被現象且不允許轉移到其他節點時，排隊節點前的工序被迫暫停工作。實際系統中，受阻原因可能是節點容量偏小或後面工序進度偏慢，Q-GERT網路的輸入類型（排隊流的到達規律）一般有確定型、隨機型和介於二者之間的中間型等。

通常排隊網路可分為如下三種基本類型：

開環網路(Open networks):至少有一個來自外部的輸入顧客流和至少一個輸出到外部的輸出顧客流，如圖8.1所示。開環網路可用於表示一個具有來自外部的到達和從內部離開的事務處理系統。

閉環網路(Closed networks):所有顧客永遠在網路內循環流動，此時網路中顧客數目為常數。例如，將圖8.1中節點1和節點2的外部線條去 掉，它就變成一個閉環網路。閉環網路可用於模擬多程序級別維持恆定情 況下的批量類型的工作負荷。

混合網路(Mixed networks):如果所研究的排隊網路對某類顧客是開放的，而對其他類顧客是關閉的。混合網路可用於同時表示計算機系統中的事務處理性和批量類型的工作負荷。

用Q-GERT網路模型分析問題的步驟為：將實際問題用網路模型描述，明確節點特性，找出突出反映排隊問題的節點；計算網路；分析評價，做出決策。求解的目的是為掌握整個網路系統排隊現象的統計規律，研究系統的運行效率，估計服務質量，決定改進措施，尋找系統處於穩定的高效的工作狀態。

Q-GERT網路模型的結構多種多樣，對一個系統來說，解決的問題不同時，其網路模型也不同，所求解的內容亦各有差異。一般難以用分析法求解，最有效的求解辦法為計算機模擬，計算機網路流在不同時刻狀態的變化情況，以及系統在每個時刻所處的狀態，然後再匯總統計，分析全周期內的工作狀態，求解的結果有：（1）輸入節點的平均到達率。（2）Q節點，包括平均排隊個數，等待的平均時間和標準差，被斥的個數，排隊中最大數量和最小數量。（3）統計節點（匯節點），包括通過該節點的個數，到達節點時間，從輸入到該節點消耗時間的均值和標準差，輸出個數與輸入個數的比率。（4）工序，包括工作效率，受阻時間，工作人員忙、閑最長時間，工作人員平均工作時間和標準差。在應用時可根據解決實際問題的要求，有選擇性的計算結果。

對排隊網路的描述有一套符號體系。例如，M/ CT/1表示顧客來到的間隔時間為負指數分佈(M)、服務時間為一般分佈(G)、單個服務台(1)等。排隊網路問題早已由電話服務系統等問題提出和發展，但難度甚大，連看來簡單的G/G/1問題至今未有通用的解法。排隊網路的狀態一般用各服務台前各類顧客排隊長度的聯合分佈來描述。只有當該聯合分佈可以分解為各個隊列長度分佈的乘積形式，即各隊長分佈相互獨立時，問題才較容易解決。因此，研究具乘積形式解的排隊網路類型是一個重要的理論和實踐的問題。例如，傑克森網路和BCMP網路(參見“BCMP網路”)都是著名的具有乘積形式解的例子。

排隊論(Queuing Theory)，或者稱為隨機服務系統理論，在計算機網路和計算機系統 的性能評價中佔有相當重要的地位，任何一個排隊模型都由3個環節組成：顧客的到達過程、服務機構和排隊規則.

到達過程通常用兩個相鄰顧客的到達時間間隔來描述。平均到達時間間隔的倒數表示單位時間內平均到達的個數，稱為到達率。常見的到達過程形式有規則到達、泊松到達、一般相同而獨立的到達、成批到達、非平穩到達和連續到達。在經典的排隊論中多假設到達過程是泊松過程。

服務機構需要明確的是服務站的個數、服務站之間的串並聯結構和服務台的服務時間分佈規律。服務時間的類別也有多種，平均服務時間的倒數表示單位時間內可以完成服務的平均次數，稱為服務率。常見的服務時間分佈有常數分佈、指數分佈、愛爾朗分佈和一般分佈，

排隊規則是指在每一個服務站等待服務的顧客按照什麼樣的順序接受服務。一個服務站的每類顧客在一個時刻最多只能有一個顧客接受服務，滿足這一條件的常見服務原則有：先到先服務原則（FIFO)、後到先服務原則（LIFO）、優先順序原則和伺服器共亨服務原則，在排隊系統研究中，隊長、顧客在系統中的等待時間以及逗留時間的長短都與服務原則有關，不同服務原則直接影響系統的穩定性和顧客在系統中耗費時間的長短，所以對於排隊系統而言，排隊規則尤其重要。

在排隊系統中，能夠反映系統結構及性能的可用於定最量分析的主要指標如表7-1所示。

其形式化描述需闡明以下幾方面特徵：

1.顧客(亦泛指待加工零件等)的種類、到來數量的特徵、優先等級和規則等.。

2.服務台(亦指加工機器等)的數量和服務時間的統計分佈。

3.排隊規則，如是否先到先服務、顧客是否因等待和服務時間過長而中途離去等。

4.排隊空間及系統中總顧客數的限制.。

5.在多服務台形成服務網路情形還有關於顧客接受多種服務的路徑和規則等，研究的課題包括系統性能指標，如平均排隊長度和顧客保留時間的統計分析、系統參數和結構設計以及調度優化的規則等。

排隊網路將行人所處的環境用“節點”和“邊”抽象表示，將複雜情況精簡，更加有利於模型的實際應用。

其缺點是：行人的移動過程很模糊，對於其中發生的碰撞，以及行人之間的相互協作問題無法體現；對於複雜的建築和設施布局的不同帶來的行人移動變化未作考慮，且“先進先出”的排隊策略未必適合於行人系統。

排隊網路模型在生產調度、計算和通信系統優化等方面有重要應用。隨機模擬試驗仍是一種主要研究途徑，最近發展了一些基於模擬的統計優化技術，可望達到實用的目的.