曼哈頓距離

圖中紅線代表曼哈頓距離，綠色代表歐氏距離，也就是直線距離，而藍色和黃色代表等價的曼哈頓距離。從一點到達另一點的距離正是在南北方向上旅行的距離加上在東西方向上旅行的距離，因此，曼哈頓距離又稱為計程車距離。曼哈頓距離不是距離不變數，當坐標軸變動時，點間的距離就會不同。曼哈頓距離示意圖在早期的計算機圖形學中，屏幕是由像素構成，是整數，點的坐標也一般是整數，原因是浮點運算很昂貴，很慢而且有誤差，如果直接使用AB的歐氏距離(歐幾里德距離：在二維和三維空間中的歐氏距離的就是兩點之間的距離），則必須要進行浮點運算，如果使用AC和CB，則只要計算加減法即可，這就大大提高了運算速度，而且不管累計運算多少次，都不會有誤差。

我們可以定義曼哈頓距離的正式意義為L1-距離或城市區塊距離，也就是在歐幾里德空間的固定直角坐標系上兩點所形成的線段對軸產生的投影的距離總和。

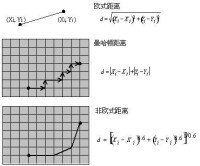
例如在平面上，坐標（x1, y1）的i點與坐標（x2, y2）的j點的曼哈頓距離為：

d(i,j)=|X1-X2|+|Y1-Y2|.

要注意的是，曼哈頓距離依賴坐標系統的轉度，而非系統在坐標軸上的平移或映射。

曼哈頓距離的命名原因是從規劃為方型建築區塊的城市（如曼哈頓）間，最短的行車路徑而來（忽略曼哈頓的單向車道以及只存在於3、14大道的斜向車道）。任何往東三區塊、往北六區塊的的路徑一定最少要走九區塊，沒有其他捷徑。

計程車幾何學滿足除了SAS全等定理之外的希爾伯特定理，SAS全等指任兩個三角型兩個邊與它們的夾角均分別對應相等，則這兩個三角型全等。

在計程車幾何學中，一個圓是由從圓心向各個固定曼哈頓距離標示出來的點圍成的區域。因此這種圓其實就是旋轉了45度的正方形。如果有一群圓，任兩圓皆相交，則整群圓必在某點相交；因此曼哈頓距離會形成一個超凸度量空間（Injective metric space）。對一個半徑為r 的圓來說，這個正方形的圓每邊長√2r。此'"圓"的半徑r對切比雪夫距離 (L∞ 空間)的二維平面來說，也是一個對座標軸來說邊長為2r的正方形，因此二維切比雪夫距離可視為等同於旋轉且放大過的二維曼哈頓距離。然而這種介於L1與L∞的相等關係並不能延伸到更高的維度。

非負性：d(i,j)≥0 距離是一個非負的數值

同一性：d(i,i)= 0 對象到自身的距離為0

對稱性：d(i,j)= d(j,i)距離是一個對稱函數

三角不等式：d(i,j)≤d(i,k)+d(k,j)從對象i到對象j的直接距離不會大於途經的任何其他對象k的距離

在西洋棋里，車（城堡）是以曼哈頓距離來計算棋盤 格上的距離；而王（國王）與后（皇后）使用切比雪夫距離，象（主教）則是用轉了45度的曼哈頓距離來算（在同色的格子上），也就是說它以斜線為行走路徑。只有國王需要一步一步走的方式移動，皇后、主教與城堡可以在一或兩次移動走到任何一格（在沒有阻礙物的情況下，且主教忽略它不能走到的另一類顏色）。

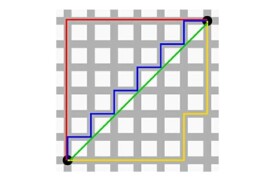
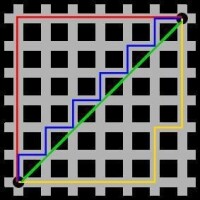
圖為曼哈頓與歐幾里德距離: 紅、藍與黃線分別表示所有曼哈頓距離都擁有一樣長度(12)，而綠線表示歐幾里德距離有6×√2 ≈ 8.48的長度。

曼哈頓距離——兩點在南北方向上的距離加上在東西方向上的距離，即d（i，j）=|xi-xj|+|yi-yj|。對於一個具有正南正北、正東正西方向規則布局的城鎮街道，從一點到達另一點的距離正是在南北方向上旅行的距離加上在東西方向上旅行的距離因此曼哈頓距離又稱為計程車距離，曼哈頓距離不是距離不變數，當坐標軸變動時，點間的距離就會不同。