特殊函數
特殊函數
特殊函數理論處理一些類似三角函數及伽瑪函數、貝塞爾函數等超幾何數列函數,具有特殊的性質和特點,在現實中得到大量的運用的函數。而這些理論的研究並不在一般數學分析或實函數分析範疇之內。傳統上對特殊函數的分析主要基於對其的數值展開基礎上。隨著電子計算的發展,這個領域內開創了新的研究方法。而李群理論也提供了對問題的新視角。
目錄
級超越函稱,函完析函稱超越函。級超越函超越函初函泛稱。殊函半尋求某程。類繁,且斷。:Γ 函、 函、超函、勒函、貝塞函。交項式,雅項式、切雪項式、埃米項式、蓋項式,,列殊函容。
殊函,程技術,計算廣泛。研究殊函具析函論,圍積、冪級數展開等等。 L.歐拉、P.-S.拉普拉斯、J.-B.-J.傅里葉等人,都在這方面做過奠基工作。
Γ函 階乘n!僅對正整數n及0有意義,擴大到任意複數α,定義階乘函數為
與階乘函數密切聯繫的是Γ函數,它的定義是:當z不為零及負整數時,
Γ(z)是亞純函數,以0,-1,-2,…為其單極點。Γ(z)滿足兩個等式:
當α不為零及負整數時,
特殊情形有
n!=(1)n=г(n+1)。
當Re(z)>0時,
當│argz│≤π-δ(δ>0),│z│→∞ 時,
在這公式中置z=n+1,就可得到斯特林公式
Γ函數是數學中常用的函數之一,許多重要級數的係數,常常用Γ函數表出。
B函數 B函數可以用Γ函數來定義:
當Re(p)>0,Re(q)>0時,
B函數可以用來計算一些定積分的值。例如,當Re(m)>0,Re(n)>0時,
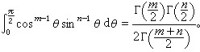
特殊函數
叫做超幾何級數。當α=b)=с=1時,它就是幾何級數。當α或b)為零或負整數時,它簡化成多項式。如果α,b)均不為零及負整數,則它是無窮冪級數,其收斂半徑為1,因而在|z|<1 中解析。這時從它出發利用解析開拓可產生完全解析函數。這樣的完全解析函數(包括多項式這一特殊情形在內)叫做超幾何函數,記作F(α,b);с;z)。這個符號也用來表示上述冪級數。若用θ表示微分運算元,則u=F(α,b);с;z)是高斯微分方程
的一個解。當Re(с)>Re(b))>0,|z|<1時,F(α,b);с;z)
設αj(j=1,2,…,p),βk(k=1,2,…,q)均為常數,且後者不為零及負整數,並設p≤q+1。冪級數
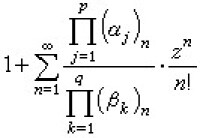
特殊函數
它是微分方程
的一個解。當p=2,q=1時,它就是超幾何函數,其餘情形叫做廣義超幾何函數。當p=q=1時,叫做合流超幾何函數。
一函數F(z,t),如果通過形式運算(即不管這種運算是否合理)能夠展成t的冪級數
不論這個級數是否收斂,只要ƒn(z)有意義,就稱F(z,t)為ƒn(z)的母函數。
廣義超幾何函數及超幾何函數可以用來表示多種初等函數、高級超越函數以及它們之中的一些母函數,因而有廣泛應用。
勒讓德函數 勒讓德微分方程
的兩個獨立解
及
(n≠負整數或負奇數的一半),分別叫做第一類及第二類勒讓德函數,並記作 Pn(z),Qn(z)。當n為正整數或零時,Pn(z)為n次多項式,叫做勒讓德多項式;而
且
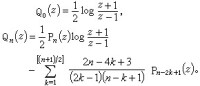
特殊函數
與勒讓德函數有密切聯繫的是連帶勒讓德函數。當m,n均為整數且0≤m ≤n時,第一類、第二類連帶勒讓德函數分別為
及
這裡z屬於在實軸的閉區間【-1,1】上有割線的z面。它們是連帶勒讓德微分方程
的兩個獨立解。當-1 這裡α為常數。他採用分離變數法解這個方程,得到貝塞爾微分方程及貝塞爾函數。數年後J.-L.拉格朗日研究行星繞日問題,19世紀初期傅里葉研究圓柱體的熱傳導問題,都用到貝塞爾函數。所謂貝塞爾微分方程就是形如
這裡α為常數。他採用分離變數法解這個方程,得到貝塞爾微分方程及貝塞爾函數。數年後J.-L.拉格朗日研究行星繞日問題,19世紀初期傅里葉研究圓柱體的熱傳導問題,都用到貝塞爾函數。所謂貝塞爾微分方程就是形如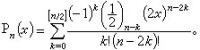 一個多項式如果能夠用一個函數的n階導數乘上適當的因子表示出來,這種表達式通常叫做這個多項式的羅德里格斯公式。Pn(x)的羅德里格斯公式是
一個多項式如果能夠用一個函數的n階導數乘上適當的因子表示出來,這種表達式通常叫做這個多項式的羅德里格斯公式。Pn(x)的羅德里格斯公式是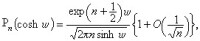 這裡O中常數可取為,其中A1,A2為絕對常數。當0≤θ≤π時,
這裡O中常數可取為,其中A1,A2為絕對常數。當0≤θ≤π時, 母函數
母函數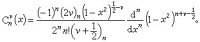 母函數
母函數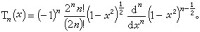 母函數
母函數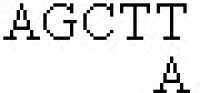 正交性 條件α>-1;區間(0,∞);權函數xαe-x。
正交性 條件α>-1;區間(0,∞);權函數xαe-x。
當m=1,2,…,n時,(cosθ)cosmφ,(cosθ)sinmφ以及Pn(cosθ)構成2n+1個線性無關的n次球面調和函數,可以用來解在球面上滿足一定邊界條件的拉普拉斯方程
所以在研究電磁、重力、速度等的勢函數以及當熱平衡時物體的溫度要用到它們。
貝塞爾函數 在18世紀中葉歐拉研究圓鼓膜振動問題時,引進了極坐標形式的波動方程
特殊函數
的方程,這裡v為常數。它的一個解是
稱為第一類貝塞爾函數。當v不為整數時,它的另一獨立解為
當v為整數n時,則規定
它們稱為第二類貝塞爾函數。
設
 (z)為兩個變數z,v的解析函數,滿足一對遞推公式
(z)為兩個變數z,v的解析函數,滿足一對遞推公式
特殊函數
特殊函數
則稱
 (z)為圓柱函數。J
(z)為圓柱函數。J (z)及Y
(z)及Y (z)均為圓柱函數。圓柱函數可以用來解在圓柱面上滿足一定邊界條件的拉普拉斯方程及波動方程。
(z)均為圓柱函數。圓柱函數可以用來解在圓柱面上滿足一定邊界條件的拉普拉斯方程及波動方程。
特殊函數
特殊函數
特殊函數
特殊函數
設φ0(x),φ1(x),…,φn(x),…為在開區間(α,b))上有定義的實函數系,ω(x)為定義在(α,b))上的非負函數;如果對任何非負整數m≠n恆有
則稱{φn(x)}為在區間(α,b))上以ω(x)為權函數的正交系。如果φn(x)恰為n次多項式,那麼φn(x)稱為正交多項式。
設v>-1,則J (z)的零點均為實數,且有無窮個正零點及負零點,其階均為1。若以j1,j2,j3,…表示J
(z)的零點均為實數,且有無窮個正零點及負零點,其階均為1。若以j1,j2,j3,…表示J (z)的正零點按上升順序的排列,則當v固定時,{J
(z)的正零點按上升順序的排列,則當v固定時,{J (jnx)}是在(0,1)上以x為權函數的正交系。
(jnx)}是在(0,1)上以x為權函數的正交系。
特殊函數
特殊函數
特殊函數
勒讓德多項式 Pn(x) 在18世紀後期勒讓德研究球體引力及行星繞日運動問題,從母函數
出發,引進了勒讓德多項式。它的常用定義是
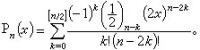
特殊函數
勒讓德多項式具有多種積分表示,常用的拉普拉斯第一積分表示為
Pn(x)具有遞推公式
Pn(x)是在區間(-1,1)中以1為權函數的正交多項式。
設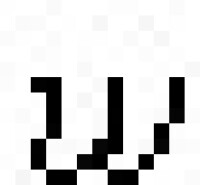 =α+iβ,α>0。當
=α+iβ,α>0。當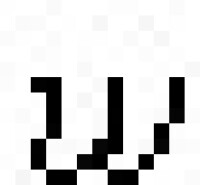 固定,n→∞時,
固定,n→∞時,
特殊函數
特殊函數
特殊函數
Pn(x)有n個單零點,在實軸的開區間(-1,1)中。利用這些零點以及在這些零點處Pń(x)的值,可以構造一種精確度很高的求定積分近似值公式。
1980年前後,有幾位數學工作者,利用勒讓德多項式,討論一些數的無理性,擴大了這個古老多項式新的應用,引起人們的重視。
雅可比多項式P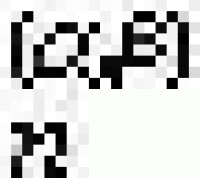 (x)
(x)
特殊函數
定義
羅德里格斯公式
特殊函數
微分方程
遞推公式
正交性 條件α>-1,β>-1;區間(-1,1);權函數(1-x)α(1+x)β。
特殊情形 格根堡多項式
勒讓德多項式
。
切比雪夫多項式。
格根堡多項式C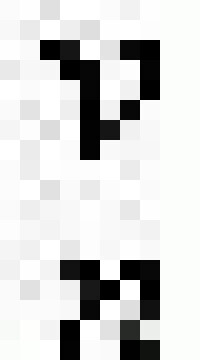 (x)
(x)
特殊函數
定義
羅德里格斯公式
特殊函數
微分方程
遞推公式
正交性 條件;區間(-1,1);權函數。
切比雪夫多項式Tn(x)
定義。
羅德里格斯公式
特殊函數
微分方程
遞推公式
,
正交性 區間(-1,1),權函數。
切比雪夫多項式在函數逼近及計算數學中用到。
埃爾米特多項式 Hn(x)
定義
羅德里格斯公式
母函數
微分方程
遞推公式
正交性 區間(-∞,∞);權函數。
拉蓋爾多項式 L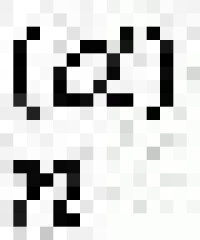 (x)
(x)
特殊函數
定義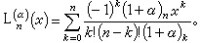
特殊函數
羅德里格斯公式
母函數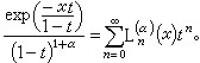
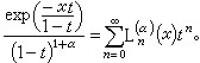
特殊函數
微分方程
特殊函數
遞推公式
特殊函數
以上所列舉的正交多項式都是經典的。在20世紀也引進了許多新的正交多項式,最引人注意的是與貝塞爾函數密切聯繫的貝塞爾多項式,其定義為它在證明er的無理性時用到,這裡r為有理數。
參考書目
小谷正雄、橋本英典著,錢瑞壯譯:《特殊函數》,上海科學技術出版社,上海,1962。(小谷正雄、橋本英典著:《特殊函數》,岩波,東京,1958。)
莫葉:關於Legendre多項式,《數學進展》,Vol.12,No.4,1983。
目錄
