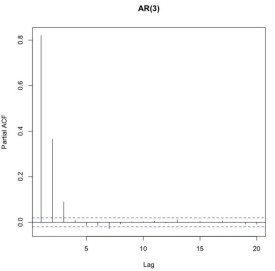
偏相關係數
偏相關係數
偏相關係數
在多元相關分析中,簡單相關係數可能不能夠真實的反映出變數X和Y之間的相關性,因為變數之間的關係很複雜,它們可能受到不止一個變數的影響。這個時候偏相關係數是一個更好的選擇。
偏相關係數是在排除了其他變數的影響下計算變數間的相關係數。假設我們需要計算X和Y之間的相關性,Z代表其他所有的變數,X和Y的偏相關係數可以認為是X和Z線性回歸得到的殘差Rx與Y和Z線性回歸得到的殘差Ry之間的簡單相關係數,即Pearson相關係數。
偏相關係數的計算可以有下面的三種方法
1 根據上面的說法,從線性回歸的角度計算變數間的偏相關係數,但是這樣做很麻煩。
2 迭代法,可以認為簡單相關係數為0階偏相關係數,任何n階偏相關都可以通過3個(n-1)階偏相關係數計算出來。
偏相關係數的檢驗可以有兩種方法。一種是t-test,另外一種fisher 轉化法。
利用偏相關係數進行變數間凈相關分析通常完成兩大步:
第一:計算樣本的偏相關係數。
利用樣本數據計算偏相關係數,反應了兩個變數間凈相關的強弱程度。在分析變數x1和x2之間的凈相關時,當控制了變數x3的線性作用后,x1和x2之間的一階偏相關係數定義為:
第二:對樣本來自的兩個總體是否存在顯著的凈相關進行推斷:
1)提出原假設,即兩總體的偏相關係數與零誤顯著差異。
式中,r為偏相關係數,n為樣本數,q為階數。統統計量服從n-q-2個自由度的t分佈。
3)計算檢驗統計量的觀測值和對應的概率p-值。
4)決策。如果檢驗統計量的概率p-值小於給定的顯著性水平α,怎應拒絕原假設,反之,則不能拒絕原假設。