約瑟夫·拉格朗日
法國著名數學家
約瑟夫徠·拉格朗日（Joseph Louis Lagrange 1736-1813），普魯士國王腓特烈大帝尊稱他為“歐洲最大之數學家”，1736年1月25日生於義大利都靈，1813年4月10日卒於巴黎。
他在數學、力學和天文學三個學科領域中都有歷史性的貢獻，其中尤以數學方面的成就最為突出。
1813年4月3日拿破崙授予他帝國大十字勳章，但此時已卧床不起，4月11日早晨逝世。
大事件
1736-01-25
出生
1736年1月25日生於義大利都靈。
1755
發展變分法，從而名聲大振
1755年19歲時在探討數學難題“等周問題”的過程中，他以歐拉的思路和結果為依據，用純分析的方法求變分極值。第一篇論文“極大和極小的方法研究”，發展了歐拉所開創的變分法，為變分法奠定了理論基礎。變分法的創立，使拉格朗日在都靈聲名大振，並使他在19歲時就當上了都靈皇家炮兵學校的教授，成為當時歐洲公認的第一流數學家。
1756
任命為普魯士科學院院士
1756年受歐拉的舉薦，拉格朗日被任命為普魯士科學院通訊院士。
1766
開始了科研的鼎盛時期
1766年德國的腓特烈大帝向發出邀請時說，在“歐洲最大的王”的宮廷中應有“歐洲最大的數學家”。於是他應邀前往柏林，任普魯士科學院數學部主任，居住達20年之久，開始了他一生科學研究的鼎盛時期。
1772
建立一階偏微分方程理論
拉格朗日是一階偏微分方程理論的建立者，他在1772年完成的。“關於一階偏微分方程的積分”和1785年完成的“一階線性偏微分方程的一般積分方法”中，系統地完成了一階偏微分方程的理論和解法。
1774
對常微分方程的奇解和特解做出歷史性貢獻
在柏林時期，他對常微分方程的奇解和特解做出歷史性貢獻，在1774年完成的“關於微分方程特解的研究”中系統地研究了奇解和通解的關係，明確提出由通解及其對積分常數的偏導數消去常數求出奇解的方法；還指出奇解為原方程積分曲線族的包絡線。當然，他的奇解理論還不完善，現代奇解理論的形式是由G.達布（Darboux）等人完成的。
1788
創立分析力學
他在所著《分析力學》(1788)中，吸收並發展了歐拉、達朗貝爾等人的研究成果，應用數學分析解決質點和質點系(包括剛體、流體)的力學問題。
1795
擔任法國最高學術機構委員會主席
1795年建立了法國最高學術機構——法蘭西研究院后，拉格朗日被選為科學院數理委員會主席。此後，他才重新進行研究工作，編寫了一批重要著作：《論任意階數值方程的解法》《解析函數論》和《函數計算講義》，總結了那一時期的特別是他自己的一系列研究工作。
1813-04-03
被拿破崙授予帝國大十字勳章
1813年4月3日拿破崙授予他帝國大十字勳章，但此時已卧床不起。
1813-04-10
去世
1813年4月10日卒於巴黎。
父親是法國陸軍騎兵里的一名軍官，後由於經商破產，家道中落。據本人回憶，如果幼年時家境富裕，他也就不會作數學研究了，因為父親一心想把他培養成為一名律師。個人卻對法律毫無興趣。
科學研究所涉及的領域極其廣泛。他在數學上最突出的貢獻是使數學分析與幾何與力學脫離開來，使數學的獨立性更為清楚，從此數學不再僅僅是其他學科的工具。
約瑟夫·拉格朗日
在柏林工作的前十年，把大量時間花在代數方程和超越方程的解法上，作出了有價值的貢獻，推動一代數學的發展。他提交給柏林科學院兩篇著名的論文：《關於解數值方程》和《關於方程的代數解法的研究》。把前人解三、四次代數方程的各種解法，總結為一套標準方法，即把方程化為低一次的方程（稱輔助方程或預解式）以求解。
也是分析力學的創立者。在其名著《分析力學》中，在總結歷史上各種力學基本原理的基礎上，發展達朗貝爾、歐拉等人研究成果，引入了勢和等勢面的概念，進一步把數學分析應用於質點和剛體力學，提出了運用於靜力學和動力學的普遍方程，引進廣義坐標的概念，建立了拉格朗日方程，把力學體系的運動方程從以力為基本概念的牛頓形式，改變為以能量為基本概念的分析力學形式，奠定了分析力學的基礎，為把力學理論推廣應用到物理學其他領域開闢了道路。
他還給出剛體在重力作用下，繞旋轉對稱軸上的定點轉動（拉格朗日陀螺）的歐拉動力學方程的解，對三體問題的求解方法有重要貢獻，解決了限制性三體運動的定型問題。對流體運動的理論也有重要貢獻，提出了描述流體運動的拉格朗日方法。
研究工作中，約有一半同天體力學有關。他用自己在分析力學中的原理和公式，建立起各類天體的運動方程。在天體運動方程的解法中，發現了三體問題運動方程的五個特解，即拉格朗日平動解。此外，他還研究了彗星和小行星的攝動問題，提出了彗星起源假說等。
近百餘年來，數學領域的許多新成就都可以直接或間接地溯源於工作。所以他在數學史上被認為是對分析數學的發展產生全面影響的數學家之一。
拉格朗日父姓拉格朗日亞（Lagrangia）。拉格朗日在都靈出生受洗記錄上的正式名字為約瑟普·洛德維科·拉格朗日亞（Giuseppe Lodovico，Lagrangia）。父名弗朗切斯科·洛德維科·拉格朗日亞（Francesco Lodovico， Lagrangia）；母名泰雷薩·格羅索（Teresa Grosso）。他曾用過的姓有德·拉·格朗日（De la Grange），拉·格朗日（La Grange）等。去世后，法蘭西研究院給他寫的頌詞中，正式用約瑟夫·拉格朗日（Joseph-Louis Lagrange ）。父係為法國後裔。曾祖是法國騎兵上校，到義大利后與羅馬家族的人結婚定居；祖父任都靈的公共事務和防務局會計，又同當地人結婚。父親也在都靈同一單位工作，共有11個子女，但大多數夭折，拉格朗日最大。
到了青年時代，在數學家雷維里的教導下，喜愛上了幾何學。17歲時，他讀了英國天文學家哈雷的介紹牛頓微積分成就的短文《論分析方法的優點》后，感覺到“分析才是自己最熱愛的學科”，從此他迷上了數學分析，開始專攻當時迅速發展的數學分析。
18歲時用義大利語寫了第一篇論文，是用牛頓二項式定理處理兩函數乘積的高階微商，他又將論文用拉丁語寫出寄給了當時在柏林科學院任職的數學家歐拉。不久后，他獲知這一成果早在半個世紀前就被萊布尼茲取得了。這個並不幸運的開端並未灰心，相反，更堅定了他投身數學分析領域的信心。
1755年19歲時在探討數學難題“等周問題”的過程中，他以歐拉的思路和結果為依據，用純分析的方法求變分極值。第一篇論文“極大和極小的方法研究”，發展了歐拉所開創的變分法，為變分法奠定了理論基礎。變分法的創立，使拉格朗日在都靈聲名大振，並使他在19歲時就當上了都靈皇家炮兵學校的教授，成為當時歐洲公認的第一流數學家。
1756年受歐拉的舉薦，拉格朗日被任命為普魯士科學院通訊院士。
1764年法國科學院懸賞徵文，要求用萬有引力解釋月球天平動問題，他的研究獲獎。接著又成功地運用微分方程理論和近似解法研究了科學院提出的一個複雜的六體問題（木星的四個衛星的運動問題），為此又一次於1766年獲獎。
1766年德國的腓特烈大帝向發出邀請時說，在“歐洲最大的王”的宮廷中應有“歐洲最大的數學家”。於是他應邀前往柏林，任普魯士科學院數學部主任，居住達20年之久，開始了他一生科學研究的鼎盛時期。在此期間，他完成了《分析力學》一書，這是牛頓之後的一部重要的經典力學著作。書中運用變分原理和分析的方法，建立起完整和諧的力學體系，使力學分析化了。他在序言中宣稱：力學已經成為分析的一個分支。
1783年故鄉建立了"都靈科學院"，他被任命為名譽院長。
1786年腓特烈大帝去世以後，他接受了法王路易十六的邀請，離開柏林，定居巴黎，直至去世。
這期間他參加了巴黎科學院成立的研究法國度量衡統一問題的委員會，並出任法國米制委員會主任。1799年，法國完成統一度量衡工作，制定了被世界公認的長度、面積、體積、質量的單位，為此做出了巨大的努力。
1795年建立了法國最高學術機構——法蘭西研究院后，拉格朗日被選為科學院數理委員會主席。此後，他才重新進行研究工作，編寫了一批重要著作：《論任意階數值方程的解法》《解析函數論》和《函數計算講義》，總結了那一時期的特別是他自己的一系列研究工作。
1813年4月3日拿破崙授予他帝國大十字勳章，但此時已卧床不起，4月11日早晨逝世。
拉格朗日在柏林期間完成了大量重大研究成果，為一生研究中的鼎盛時期，多數論文在上述兩刊物中發表，少量仍寄回都靈。其中有關月球運動（三體問題）、行星運動、軌道計算、兩個不動中心問題、流體力學、數論、方程論、微分方程、函數論等方面的成果，成為這些領域的開創性或奠基性研究。此外，還在概率論、循環級數以及一些力學和幾何學課題方面有重要貢獻。他還翻譯了歐拉和A．棣莫弗（De Moivre）的著作。1782年給P．拉普拉斯（Laplace）的信中說：“我幾乎寫完《分析力學論述》（Traitéde Mécanique Analytique），但無法出版。”拉普拉斯安排在巴黎出版，出書時已是1788年，拉格朗日已到巴黎了。此書成為分析力學的奠基著作。
1783年，老家建立“都靈科學院”，任命拉格朗日為名譽院長。原出版刊物改為《都靈科學院綜合論叢》（Mélanges des l’Acade-mie des sciences des Turin）。拉格朗日也常寄論文回去發表。到1786年8月，因支持他的普魯士國王腓特烈二世去世，決定離開柏林。他於1787年5月18日應巴黎科學院邀請動身去法國。
巴黎時期（1787—1813）。拉格朗日1787年7月29日正式到巴黎科學院工作。由於他從1772年起就是該院副院士，這次來工作受到了更熱情的歡迎，可惜達朗貝爾已在1783年去世。
到巴黎的前幾年，他主要學習更廣泛的知識，如形而上學、歷史、宗教、醫藥和植物學等。1789年爆發資產階級革命，他只是有興趣地旁觀。1790年5月8日的制憲大會上通過了十進位的公製法，科學院建立相應的“度量衡委員會”，拉格朗日為委員之一。8月8日，國民議會決定對科學院專政，三個月後又決定把A. L. 拉瓦錫（Lavoisier），拉普拉斯，C. A. 庫倫（Coulomb）等著名院士清除出科學院。但拉格朗日被保留，並任度量衡委員會主席。
1792年，喪偶9年的拉格朗日同天文學家勒莫尼埃（LeMonnier）的女兒何蕾-弗朗索瓦-阿德萊德（Renée-Francoise- Adelaide）結婚，雖未生兒女，但家庭幸福。
1793年9月政府決定逮捕所有在敵國出生的人，經拉瓦錫竭力向當局說明后，把拉格朗日作為例外。
1794年5月7日法國雅各賓派開庭審判波旁王朝包稅組織人物，把包括拉瓦錫在內的28名成員全部處以死刑，拉格朗日等人儘力地挽救，請求赦免，但是遭到了革命法庭副長官考費那爾（J.B.Coffinhal）的拒絕，全部予以駁回，並宣稱，“共和國不需要學者，而只需要為國家而採取的正義行動！”第二天5月8日的早晨，拉格朗日痛心地說：“他們可以一眨眼就把拉瓦錫的頭砍下來，但他那樣的頭腦一百年也再長不出一個來了。”
1795年成立國家經度局，統一管理全國航海、天文研究和度量衡委員會，拉格朗日是委員之一。同年成立的兩個法國最高學府：師範學校和綜合工科學校中，拉格朗日等為首批教授。在取消對科學院的專政后，1795年建立了法國最高學術機構——法蘭西研究院，選舉拉格朗日為第一分院（即科學院）的數理委員會主席。此後他才重新進行研究工作，但主要是整理過去的工作，並結合教材編寫完成一批重要著作。
《分析力學論述》於1788年出版后，拉格朗日就著手把書中的原理和方法推廣到一般的情況。他在1810年前發表的一些論文，
如在《法蘭西學院文獻》（Memoires de l' Institute）中刊登的“關於任意常數變異法在所有力學問題中的一般理論”（Memoirs surla théorie génèrale de la variatiou des constantes arbitrairesdans tons les problèmes de la mécanique，1809年3月宣讀）等，都是為修改出第二版作準備。第二版更名為《分析力學》（Mé-canique analytique），分兩卷，上卷於1811年出版，下卷直到1816年才印出，拉格朗日已去世三年。
他在師範學校的教材《師範學校數學基礎教程》（Les le consélèmentaires sur les Mathématique donnés à l' cole Normale）於1796年出版，後來收進《拉格朗日文集》（Oeuvres de Lagrange，下面簡稱《文集》），第七卷的內容他在1812年做過大量充實。
1798年出版的《論任意階數值方程的解法》（Traité de la résolution des éqnations numériques de tous les degrés），總結了早年在方程式論方面的成果，並加以系統化，充實後於1808年再版。
關於函數論方面他出版了兩本歷史性著作。一是《解析函數論，含有微分學的主要定理，不用無窮小，或用在消失的量，或極限與留數等概念，而掃結為代數分析藝術》（Theorie des fonctionsanalytiques，contenant les principes du calcul diffèrentiel dégagés de toute considération d'infiniment petits， d'éranouissa-nts，de limites et de fluxions，et réduits à l'analyse algébrique de quantités finies），1797年出版，1813年再版；另一本《函數計算教程》（Lecons sur le calcul des fonctions），1801年出版，由師範學校講義改編。
1799年霧月政變后，拿破崙（Napoleon）提名拉格朗日等著名科學家為上議院議員及新設的勛級會榮譽軍團成員，封為伯爵；還在1813年4月3日授予他帝國大十字勳章。此時拉格朗日已重病在身，終於在4月11日晨逝世。在葬禮上，由議長拉普拉斯代表上議院，院長拉賽佩德（Lacépède）代表法蘭西研究院致悼詞。義大利各大學都舉行了紀念活動，但柏林未進行任何活動，因當時普魯士加入反法聯盟。
著作非常多，未能全部收集。他去世后，法蘭西研究院集中了他留在學院內的全部著作，編輯出版了十四卷《拉格朗日文集》，由J．A．塞雷（Serret）主編，1867年出第一卷，到1892年才印出第十四卷。
第一卷收集他在都靈時期的工作，發表在《論叢》第一到第四卷中的論文；第二卷收集他發表在《論叢》第四、五卷及《都靈科學院文獻》第一、二卷中的論文；第三卷中有他在《柏林科學院文獻》（1768—1769年，1770—1773年）發表的論文；第四卷刊有他在《柏林科學院新文獻》（1774—1779年，1781年，1783）年發表的論文；第五卷刊載上述刊物（1780—1783年，1785—1786年，1792年，1793年，1803年）發表的論文；第六卷載有他未在巴黎科學院或法蘭西研究院的刊物上發表過的文章；第七卷主要刊登他在師範學校的報告；第八卷為1808年完成的《各階數值方程的解法論述及代數方程式的幾點說明》（Traité des équations numériquesde tous les degrés， avec des notes sur plusieurs points de lathéorie des equations algébriques）一書；第九卷是1813年再版的《解析函數論，含有微分學的主要定理，不用無窮小，或正在消失的量，或極限與流數等概念，而歸結為代數分析藝術》一書；第十卷是1806年出版的《函數計算教程》一書；第十一卷是1811年出版的《分析力學》第一卷，並由J．貝特朗(Bertrand)和G．達布（Darboux）作了註釋；第十二卷為《分析力學》的第二卷，仍由上述二人註釋，此二卷書後來在巴黎重印（1965）；第十三卷刊載他同達朗貝爾的學術通訊；第十四卷是他同孔多塞，拉普拉斯，歐拉等人的學術通訊，此二卷都由L．拉朗（Lalanne）作註釋。還計劃出第十五卷，包含1892年以後找到的通訊，但未出版。
拉格朗日在數學、力學和天文學三個學科中都有重大歷史性貢獻，但他主要是數學家，研究力學和天文學的目的是表明數學分析的威力。全部著作、論文、學術報告記錄、學術通訊超過500篇。
拉格朗日的學術生涯主要在18世紀後半期。當對數學、物理學和天文學是自然科學主體。數學的主流是由微積分發展起來的數學分析，以歐洲大陸為中心；物理學的主流是力學；天文學的主流是天體力學。數學分析的發展使力學和天體力學深化，而力學和天體力學的課題又成為數學分析發展的動力。當時的自然科學代表人物都在此三個學科做出了歷史性重大貢獻。下面就拉格朗日的主要貢獻分別評述。
數學分析的開拓者
牛頓和萊布尼茲以後的歐洲數學分裂為兩派。英國仍堅持牛頓在《自然哲學中的數學原理》中的幾何方法，進展緩慢；歐洲大陸則按萊布尼茲創立的分析方法（當時包括代數方法），進展很快，當時叫分析學（analysis）。拉格朗日是僅次於歐拉的最大開拓者，在18世紀創立的主要分支中都有開拓性貢獻。
變分法
這是拉格朗日最早研究的領域，以歐拉的思路和結果為依據，但從純分析方法出發，得到更完善的結果。他的第一篇論文“極大和極小的方法研究”（Recherches sur la méthode demaximis et minimies）[2]是他研究變分法的序幕； 1760年發表的“關於確定不定積分式的極大極小的一種新方法”（Essai d'unenouvelle méthode pour déterminer les maxima et les minima desformules integrales indéfinies）[3]是用分析方法建立變分法的代表作。發表前寫信給歐拉時，稱此文中的方法為“變分方法”（themethod of variation）。歐拉肯定了，並在他自己的論文中正式將此方法命名為“變分法”（the calculus of variation）。變分法這個分支才真正建立起來。
拉格朗日方法是對積分進行極值化，函數y=y(x)待定。他不像歐拉和前人用改變極大或極小化曲線的個別坐標的辦法，而是引進通過端點(x1，y1)，(x2，y2)的新曲線y(x)+δy(x)，δy(x)叫曲線y(x)的變分。J相應的增量△J按δy，δy′展開的一、二階項叫一次變分δJ和二次變分δ2J。他用分析方法證明了δJ為零的必要條件就是歐拉方程
他達繼續討論了端點變動時的情況以及兩個自變數的重積分的情況，使這個分支繼續發展。1770年以後，拉格朗日達研究了被積函數f包含高階導數的單重和多重積分時的情況，已發展成為變分法的標準內容。
微分方程
早在都靈時期，拉格朗日就對變係數常微分方程研究做出重大成果。他在降階過程中提出了以後所稱的伴隨方程，並證明了非齊次線性變係數方程的伴隨方程的伴隨方程，就是原方程的齊次方程。他還把歐拉關於常係數齊次方程的結果推廣到變係數情況，證明了變係數齊次方程的通解可用一些獨立特解乘上任意常數相加而成；而且在知道方程的m個特解后，可以把方程降低m價。
在柏林時期，他對常微分方程的奇解和特解做出歷史性貢獻，在1774年完成的“關於微分方程特解的研究”（Sur les intégralesparticulieres des equations différentielles）[22]中系統地研究了奇解和通解的關係，明確提出由通解及其對積分常數的偏導數消去常數求出奇解的方法；還指出奇解為原方程積分曲線族的包絡線。當然，他的奇解理論還不完善，現代奇解理論的形式是由G.達布（Darboux）等人完成的。
常微分方程組的研究在當時結合天體力學中的課題進行。拉格朗日在1772年完成的“論三體問題”（Essai sur le problémedes trois corps）[8]中，找出了三體運動的常微分方程組的五個特解：三個是三體共線情況；兩個是三體保持等邊三角形；在天體力學中稱為拉格朗日平動解。他同拉普拉斯一起完善的任意常數變異法，對多體問題方程組的近似解有重大作用，促進了攝動理論的建立。
拉格朗日是一階偏微分方程理論的建立者，他在1772年完成的。“關於一階偏微分方程的積分”（Sur l'integration des équationau differences partielles du premier order）[21]和1785年完成的“一階線性偏微分方程的一般積分方法”（Méthode génèrale pourintégrer les equations partielles du premier order lorsque cesdifferences ne sont que linèaires）[23]中，系統地完成了一階偏微分方程的理論和解法。
他首先提出了一階非線性偏微分方程的解分類為完全解、奇解、通積分等，並給出它們之間的關係。後來又進一步證明了解線性方程Pp+Qq=R(P，Q，R為x，y，z的函數)(5)與解等價，而解(6)式又與解常微分方程組等價。(5)式至今仍稱為拉格朗日方程。有趣的是，由上面已可看出，一階非線性偏微分方程，可以化為解常微分方程組。但拉格朗日自己卻不明確，他在1785年解一個特殊的一階偏微分方程時，還說不能用這種方法，可能他忘記了自己在1772年的結果。現代也有時稱此方法為拉格朗日方法，又稱為柯西(Cauchy)的特徵方法。因拉格朗日只討論兩個自變數情況，在推廣到n個自變數時遇到困難，而後來由柯西在1819年克服。
方程論
18世紀的代數學從屬於分析，方程論是其中的活躍領域。拉格朗日在柏林的前十年，大量時間花在代數方程和超越方程的解法上。
他在代數方程解法中有歷史性貢獻。在長篇論文“關於方程的代數解法的思考”（Réflexions sur le resolution algébrique desequations，《全集》Ⅲ， pp 205—421）中，把前人解三、四次代數方程的各種解法，總結為一套標準方法，而且還分析出一般三、四次方程能用代數方法解出的原因。三次方程有一個二次輔助方程，其解為三次方程根的函數，在根的置換下只有兩個值；四次方程的輔助方程的解則在根的置換下只有三個不同值，因而輔助方程為三次方程。拉格朗日稱輔助方程的解為原方程根的預解函數（是有理函數）。他繼續尋找5次方程的預解函數，希望這個函數是低於5次的方程的解，但沒有成功。儘管如此，拉格朗日的想法已蘊含著置換群概念，而且使預解（有理）函數值不變的置換構成子群，子群的階是原置換群階的因子。因而拉格朗日是群論的先驅。他的思想為後來的N.H.阿貝爾（Abel）和E.伽羅瓦（Galois）採用並發展，終於解決了高於四次的一般方程為何不能用代數方法求解的問題。
拉格朗日在1770年還提出一種超越方程的級數解法。設p為方程，這就是後來在天體力學中常用的拉格朗日級數。他自己沒有討論收斂性，後來由柯西求出此級數的收斂範圍。
數論
拉格朗日到柏林初期就開始研究數論，第一篇論文“二階不定問題的解”（Sur la solution des problémès in détèrminésdu seconde degrés）[14]和送交都靈《論叢》的“一個算術問題的解”（Solution d'un problème d'arithmetique）[15]中，討論了歐拉多年從事的費馬(Fermat)方程x2-Ay2=1(x，y，A為整數)，(9)
不定問題解的新方法”(Nouvelle méthode pour resoudveles problèmes indéteminés en nombres entiers)[16]中得到更一般的費馬方程 (B也為整數)(10)的解。還討論了更廣泛的二元二次整係數方程，(11)並解決了整數解問題。
拉格朗日還在1772年的“一個算術定理的證明”（De monstration d'un théorème d'arthmétique，《文集》Ⅲ，pp.189—201）中，把歐拉40多年沒有解決的費馬另一猜想“一個正整數能表示為最多四個平方數的和”證明出來。在1773年發表的“質數的一個新定理的證明”（Démonstation d'un theorem nouveau concernant les nombres premiers）[17]中，證明了著名的定理：n是質數的充要條件為(n-1)！+1能被n整除。
拉格朗日不僅有大量成果，還在方法上有創新。如在證明(9)式研究”（Recherches d'arithmétiques，《文集》Ⅲ，pp.695—795）中，研究(11)式解時採用的方法和結果，是二次型理論的基本文獻。
函數和無窮級數
同18世紀的其他數學家一樣，拉格朗日也認為函數可以展開為無窮級數，而無窮級數則是多項式的推廣。他還試圖用代數建立微積分的基礎。在他的《解析函數論……》（《文集》Ⅸ）中，書名上加的小標題“含有微分學的主要定理，不用無窮小，或正在消失的量，或極限與流數等概念，而歸結為代數分析藝術”，表明了他的觀點。由於迴避了極限和級數收斂性問題，當然就不可能建立真正的級數理論和函數論，但是他們的一些處理方法和結果仍然有用，他們的觀點也在發展。
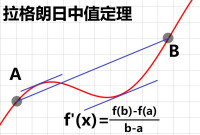
拉格朗日就在《解析函數論……》中，第一次得到微分中值定理（書中第六章）f(b)-f(a)=f′(c)(b-a)(a≤c≤b)，(12)後面並用它推導出泰勒（Taylor）級數，還給出余項Rn的具體表達式（第二十章）Rn就是著名的拉格朗日余項形式。他還著重指出，泰勒級數不考慮余項是不能用的。雖然他還沒有考慮收斂性，甚至各階導數的存在性，但他強調Rn要趨於零。表明他已注意到收斂問題。
他同歐拉、達朗貝爾等在任意函數能否表為三角級數的長期爭論，雖未解決，但為以後三角級數理論的建立打下了基礎。
拉格朗日內插公式
徠最後要提一下他在《師範學校數學基礎教程》中，提出了著名的拉格朗日內插公式。
直到現在計算機計算大量中點內插時仍在使用。另外在求多元函數相對極大極小及解微分方程中的拉格朗日任意乘子法，至今也在用。
其他
除了對數學分析在18世紀建立的主要分支有開拓性貢獻外，他對嚴格化問題也開始注意。儘管迴避了極限概念，但他仍承認可以在極限基礎上建立微積分（《文集》Ⅰ，p.325）。但正是對嚴格化重視不夠，所建立的分支到一定階段就很難深入。這可能是他晚年研究工作少的原因。他在1781年9月21日給達朗貝爾的信中說：“在我看來，似乎（數學）礦井已挖掘很深了，除非發現新礦脈，否則勢必放棄它……”（《文集》XⅢ368）這說出了他和其他同事們的心情。事實表明，19世紀在建立數學分析嚴格基礎后，數學更迅速地發展。
分析力學的創立者
他在所著《分析力學》(1788)中，吸收並發展了歐拉、達朗貝爾等人的研究成果，應用數學分析解決質點和質點系(包括剛體、流體)的力學問題。他在總結靜力學的各種原理，包括他1764年建立的虛速度原理的基礎上提出分析靜力學的一般原理，即虛功原理，並同達朗伯原理結合而得到動力學普遍方程。對於有約束的力學系統，他採用適當的變換，引入廣義坐標，得到一般的運動方程，即第一類和第二類拉格朗日方程。全書用數學分析形式寫成，沒有一幅圖，故名《分析力學》。書中還給出多自由度系統平衡位置附近微振動的基本理論，但對振動特徵方程有重根情況說得不確切，這個錯誤直到19世紀中葉才分別由K．維爾斯特拉斯(1858)和O．H．索莫夫(1859)作了改正。拉格朗日繼歐拉之後研究過理想流體運動方程，並最先提出速度勢和流函數的慨念，成為流體無旋運動理論的基礎。他在《分析力學》中從動力學普遍方程導出的流體運動方程，著眼於流體質點，描述每個流體質點自始至終的運動過程。這種方法現在稱為拉格朗日方法，以區別著眼於空間點的歐拉方法，但實際上這種方法歐拉也應用過。拉格朗日研究過重剛體定點轉動並對剛體的慣性橢球是旋轉橢球且重心在對稱軸上的情況作過詳細的分析。這種情況稱為重剛體的拉格朗日情況。這一研究在他生前未發表，后經J．比奈整理，收在《分折力學》第二版(1818)的附錄中。在此以前，泊松在1811年曾獨立得到同樣的結果。拉格朗日在1811年還導得彈性薄板的平衡方程。
天體力學的奠基者
天體力學是在牛頓發表萬有引力定律（1687）時誕生的，很快成為天文學的主流。它的學科內容和基本理論是在18世紀後期建立的。主要奠基者為歐拉，A.C.克萊羅（Clairaut）、達朗貝爾、拉格朗日和拉普拉斯。最後由拉普拉斯集大成而正式建立經典天體力學。拉格朗日一生的研究工作中，約有一半同天體力學有關，但他主要是數學家，他要把力學作為數學分析的一個分支，而又把天體力學作為力學的一個分支對待。雖然如此，他在天體力學的奠基過程中，仍有重大歷史性貢獻。
首先在建立天體運動方程上，拉格朗日用他在分析力學中的原理和(16)，(17)式，建立起各類天體的運動方程。其中特別是根據他在微分方程解法的任意常數變異法，建立了以天體橢圓軌道根數為基本變數的運動方程，仍稱作拉格朗日行星運動方程，並在廣泛應用，此方程對攝動理論的建立和完善起了重大作用，方程在1780年獲巴黎科學院獎的論文“彗星在行星作用下的攝動理論研究”（Recherches sur la théorie des perturbations queles comètes peuvent éprouver par l'action des planètes）[13]中給出，得到達朗貝爾和拉普拉斯的高度評價。另外在一篇有關三體問題的獲獎文章中[8]，把三體問題的運動方程組第一次降到七階。
在天體運動方程解法中，拉格朗日的重大歷史性貢獻是發現三體問題運動方程的五個特解[8]，即拉格朗日平動解。其中兩個解是三體圍繞質量中心作橢圓運動過程中，永遠保持等邊三角形。他的這個理論結果在100多年後得到證實。1907年2月22日，德國海德堡天文台發現了一顆小行星[後來命名為希臘神話中的大力士阿基里斯（Achilles），編號588]，它的位置正好與太陽和木星形成等邊三角形。到1970年前，已發現15顆這樣的小行星，都以希臘神話中特洛伊(Troy)戰爭中將帥們的名字命名。有9顆位於木星軌道上前面60°處的拉格朗日特解附近，名為希臘人(Greek)群；有6顆位於木星軌道上後面60°處的解附近，名為脫羅央（Trojan）群。1970年以後又繼續發現40多顆小行星位於此兩群內，其中我國紫金山天文台發現四顆，但尚未命名。至於為什麼在特解附近仍有小行星，是因為這兩個特解是穩定的。1961年又在月球軌道前後發現與地月組成等邊三角形解處聚集的流星物質，是拉格朗日特解的又一證明。至今尚未找到肯定在三個拉格朗日共線群（三體共線情況）處附近的天體，因為這三個特解不穩定。另外，拉格朗日在一階攝動理論中也有重要貢獻，提出了計算長期攝動方法（《文集》Ⅴ，pp.125—414），並與拉普拉斯一起提出了在一階攝動下的太陽系穩定性定理（參見《世界著名科學家傳記·天文學家Ⅰ》中“拉普拉斯”條）。此外，拉格朗日級數(8)式在攝動理論中有廣泛應用。
在具體天體的運動研究中，拉格朗日也有大量重要貢獻，其中大部分是參加巴黎科學院征獎的課題。他的月球運動理論研究論文多次獲獎。1763年完成的“月球天平動研究”（Recherches sur laLibration de la lune）[6]獲1764年度獎，此文較好地解釋了月球自轉和公轉的角速度差異，但對月球赤道和軌道面的轉動規律解釋得不夠好。後來在1780年完成的論文解決得更好（參見《文集》Ⅴ，pp.5—123）。獲1772年度獎的就是著名的三體問題論文[8]，也是針對月球運動研究寫出的。獲1774年度獎的論文為“關於月球運動的長期差”（Sur l’equation séculaire de la lune）[9]，其中第一次討論了地球形狀和所有大行星對月球的攝動。關於行星和彗星運動的論文也有兩次獲獎。1776年度獲獎的是他在1775年完成的三篇論文[10，11，12，]其中討論了行星軌道交點和傾角的長期變化對彗星運動的影響。1780年度的獲獎論文就是提出著名的拉格朗日行星運動方程的那篇[13]。獲1766年度獎的論文是“木星的衛星運動的偏差研究……”（Recherches sur les inégualités des satellites de Jupiter…）[7]，其中第一次討論了太陽引力對木星的四個衛星運動的影響，結果比達朗貝爾的更好。
從事的天體力學課題還有很多，如在柏林時期的前半部分，還研究了用三個時刻的觀測資料計算彗星軌道的方法（《文集》Ⅳ，pp.439—532），所得結果成為軌道計算的基礎。另外他還得到了一種力學模型——兩個不動中心問題的解，這是歐拉已討論過的，又稱為歐拉問題。是拉格朗日推廣到存在離心力的情況，故後來又稱為拉格朗日問題（《文集》Ⅱ，pp.67—121）。這些模型仍在應用。有人用作人造衛星運動的近似力學模型。此外，他在《分析力學》中給出的流體靜力學的結果，後來成為討論天體形狀理論的基礎。
總的看來，拉格朗日在天體力學的五個奠基者中，所做的歷史性貢獻僅次於拉普拉斯。他創立的“分析力學”對以後天體力學的發展有深遠的影響。
拉格朗日是18世紀的偉大科學家，在數學、力學和天文學三個學科中都有歷史性的重大貢獻。但他主要是數學家，拿破崙曾稱讚他是“一座高聳在數學界的金字塔”，他最突出的貢獻是在把數學分析的基礎脫離幾何與力學方面起了決定性的作用。使數學的獨立性更為清楚，而不僅是其他學科的工具。同時在使天文學力學化、力學分析化上也起了歷史性作用，促使力學和天文學（天體力學）更深入發展。由於歷史的局限，嚴密性不夠妨礙著他取得更多的成果。
基本信息
- 中文名
- 約瑟夫·拉格朗日
- 外文名
- Joseph-Louis Lagrange
- 別名
- 拉格朗日
- 國籍
- 法國
- 性別
- 男
- 出生地
- 義大利都靈
- 出生日期
- 1736-01-25
- 去世日期
- 1813-04-10
- 職業
- 數學家、物理學家
- 主要成就
- 拉格朗日中值定理等、數學分析的開拓者