層流和紊流

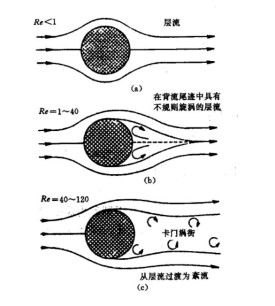
表徵液流慣性力與粘滯力相對大小，可用以判別流動形態的無因次數，記作Re。雷諾數的定義式為：Re=ρvd/μ　式中ρ、μ為液體的密度和動力粘滯係數；v、d為流動的特徵速度和特徵長度。雷諾數小時，粘性效應在整個流場中起主要作用，流動為層流。雷諾數大時，紊動混摻起決定作用，流動為紊流。對於同樣的液流裝置，由層流轉換為紊流時的雷諾數恆大於紊流向層流轉換的雷諾數。前者稱上臨界雷諾數，其值隨試驗條件而變，很不穩定；後者稱下臨界雷諾數，其值比較穩定，對於一般條件下的管流（圓管直徑為特徵長度，斷面平均流速為特徵速度），約為2300。

層流

只存在粘滯切應力。在簡單的剪切流中，粘滯切應力：μ

式中

為剪切變形速度，亦即速度沿垂直方向的變化率；μ為動力粘滯係數，只和液體種類及溫度有關的常數。此式表達了著名的牛頓內摩擦定律。層流中摩擦阻力及沿程水頭損失均與流速的一次方成正比，流速分佈呈拋物線型。圓管層流流速分佈如圖1所示。

紊流

又稱湍流。液體運動呈隨機性，即速度、壓強等均隨時間、空間作不規則的脈動，是紊流的基本特徵（圖2）。可採用時間平均法，將任一物理量的瞬時值分解為時均值與脈動值，即：

式中u∞、ū∞、u'分別為某一點處沿x方向的瞬時流速、時均流速與脈動流速；p、圴、p'分別為某點處的瞬時壓強、時均壓強與脈動壓強；T為適當選取進行平均的時段。

紊流中除粘滯切應力τ1外，還有紊流附加切應力τt。由納維－斯托克斯方程導出紊流時均運動的雷諾方程，就會增添紊流附加應力，又稱雷諾應力。如紊流時均速度分量僅有ūx=ūx(y)，則有：式中vt為紊動交換係數或渦旋運動粘滯係數。和運動粘滯係數υ不同，它不是單由物性決定的常數，而是和流動狀態有關的變數。

關於τt或vt的計算，常用L.普朗特提出的動量傳遞理論，即：式中l為混合長。顯然。按照動量傳遞理論結合實驗，已導出紊流的對數型速度分佈公式，與實驗結果比較接近。與層流相比較，紊流流速分佈趨於均勻，摩擦阻力和水頭損失增大，在充分發展的紊流中，沿程水頭損失與流速的二次方成正比。