Turbo碼
Turbo碼
編碼理論研究長期沿襲通道截止速率(Cutoff Rate)的傳統觀念,儘管各種複雜的編碼方法不斷湧現,但是超出香農限若干分貝的性能差距總是被巨大的計算複雜度阻擋而難以逾越。而Turbo碼的出現突破了這些傳統觀念的束縛和技術壁壘,在編碼理論和迭代處理技術上巧妙地另闢蹊徑,開創了通道編碼以及相關領域研究的一個新紀元。
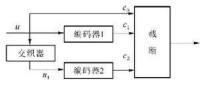
Turbo碼是Claude.Berrou等人在1993年首次提出的一種級聯碼。基本原理是編碼器通過交織器把兩個分量編碼器進行并行級聯,兩個分量編碼器分別輸出相應的校驗位比特;解碼器在兩個分量解碼器之間進行迭代解碼,分量解碼器之間傳遞去掉正反饋的外信息,這樣整個解碼過程類似渦輪(Turbo)工作。因此,這個編碼方法又被形象地稱為Turbo碼。Turbo碼具有卓越的糾錯性能,性能接近香農限,而且編解碼的複雜度不高。
Turbo 碼巧妙地將兩個簡單分量碼通過偽隨機交織器并行級聯來構造具有偽隨機特性的長碼,並通過在兩個軟入/軟出(SISO)解碼器之間進行多次迭代實現了偽隨機解碼。他的性能遠遠超過了其他的編碼方式,得到了廣泛的關注和發展,並對當今的編碼理論和研究方法產生了深遠的影響,通道編碼學也隨之進入了一個新的階段。
Shannon 編碼定理指出:如果採用足夠長的隨機編碼,就能逼近Shannon 通道容量。但是傳統的編碼都有規則的代數結構,遠遠談不上“隨機”;同時,出於解碼複雜度的考慮,碼長也不可能太長。所以傳統的通道編碼性能與通道容量之間都有較大的差距。事實上,長期以來通道容量僅作為一個理論極限存在,實際的編碼方案設計和評估都沒有以Shannon限為依據。
Turbo碼
模擬結果表明,在AWGN 通道下,碼率為 的Turbo 碼在達到誤比特率時,僅為約0.7dB (這種情況下達到通道容量的理想Eb/N0值為0db),遠遠超過了其他的編碼方式,一時在信息和編碼理論界引起了轟動。
從此以後,Turbo 碼得到了廣泛的關注和發展,並對當今的編碼理論和研究方法產生了深遠的影響,通道編碼學也隨之進入了一個新的階段。
Turbo碼由於其近Shannon界的突出糾錯能力,成為近年通道編碼理論研究的熱點問題。其編碼器由兩個(或多個)帶反饋的系統卷積碼器經一交織器并行級聯而成,接收端一般採用逐位最大后驗概率解碼器通過反覆迭代循環來解碼。
本文首先對Turbo碼的編碼原理進行了闡述和舉例,進而重點講解了Turbo碼解碼的原理,對比了MAP解碼演演算法和SOVA解碼演演算法。由以上的分析得出了很多重要的結論:如Turbo碼採用反饋卷積碼是為了獲得更大的交織增益;Turbo碼的性能主要取決於它的有效自由距離;Turbo碼在低信噪比下具有近Shannon界糾錯能力的原因;自由距離較低引起Turbo碼在中信噪比下出現糾錯平台現象等等。
對於Turbo碼的研究最初集中於對於其解碼演演算法、性能界和獨特編碼結構的研究上,經過十多年來的發展歷程,已經取得了很大的成果,在各方面也都走向使用階段。Turbo碼由於很好地應用了香農通道編碼定理中的隨機性編解碼條件而獲得了接近香農理論極限的解碼性能。它不僅在信噪比較低的高雜訊環境下性能優越,而且具有很強的抗衰落、抗干擾能力。目前,Turbo碼的研究主要集中在以下幾個方面:
編碼方面主要包括對并行級聯編碼與串列級聯編碼的分析,以及對混合級聯方式的研究;解碼方面主要包括迭代解碼、解碼演演算法(最大后驗概率演演算法MAP、修正的MAP演演算法Max-Log-MAP、軟輸出Viterbi演演算法SOVA等)的研究。
主要包括交織器的設計、碼的級聯方式、解碼演演算法、Turbo碼的性能分析等。在性能分析中,主要對碼重分佈及距離譜進行分析,但由於沒有相應的理論支持,這種分析只能是近似的,且僅局限於短碼長、小碼重的情況。
Turbo 碼在直擴(CDMA) 系統中的研究及應用
Turbo 碼不僅在通道信噪比很低的高雜訊環境下性能優越,而且還具有很強的抗衰落、抗干擾能力,因此它在通道條件差的移動通信系統中有很大的應用潛力,在第三代移動通信系統(IMT-2000)中己經將Turbo碼作為其傳輸高速數據的通道編碼標準。第三代移動通信系統(IMT-2000)的特點是多媒體和智能化,要能提供多元傳輸速率、高性能、高質量的服務,為支持大數據量的多媒體業務,必須在布限帶寬通道上傳輸數據。由於無線通道傳輸媒質的不穩定性及雜訊的不確定性,一般的糾錯碼很難達到較高要求的解碼性能(一般要求比特誤碼率小於10-6e),而Turbo碼引起超乎尋常的優異解碼性能,可以糾正高速率數據傳輸時發生的誤碼。另外,由於在直擴(CDMA) 系統中採用Turbo 碼技術可以進一步提高系統的容量,所以有關Turbo碼在直擴(CDMA) 系統中的應用,也就受到了各國學者的重視。
主要面向分組的Turbo 碼的構造、解碼及解碼器的分析。
包括Turbo 碼與調製技術(如網格編碼調製TCM)的結合、Turbo碼與均衡技術的結合(Turbo碼均衡)、Turbo碼編碼與信源編碼的結合、Turbo碼解碼與接收檢測的結合等等。Turbo碼與OFDM調製、差分檢測技術相結合,具有較高的頻率利用率,可有效地抑制短波通道中多徑時延、頻率選擇性衰落、人為干擾與雜訊帶來的不利影響。國內在Turbo碼的研究領域也取得了一定的成果和進展,西安電子科技大學綜合業務網國家重點試驗室在Turbo碼的理論和應用研究方面取得了很多研究成果。此外,清華大學、北京郵電大學和上海交通大學等高校都在進行Turbo碼相關的其它關鍵技術的研究方面取得一定的進展。深圳華為公司等在推動Turbo碼在移動通信系統中的應用方面起了積極的作用。
Turbo碼
Max-Log-MAP、Log-MAP和SOVA(Soft Output Viterbi Algorithm)演演算法。MAP演演算法是1974年被用於卷積碼的解碼,但用作Turbo碼的解碼還是要做一些修改;Max-Log-MAP與Log-MAP是根據MAP演演算法在運算量上做了重大改進,雖然性能有些下降,但使得Turbo碼的解碼複雜度大大的降低了,更加適合於實際系統的運用;Viterbi演演算法並不適合Turbo碼的解碼,原因就是沒有每比特譯出的可靠性信息輸出,修改後的具有軟信息輸出的SOVA演演算法,就正好適合了Turbo碼的解碼。這些演演算法在複雜度上和性能上具有一定的差異,系統地了解這些演演算法的原理是對Turbo碼研究的基礎,同時對這些演演算法的複雜度和性能的比較研究也將有助於Turbo的應用研究。
Turbo碼的模擬一般參考吳宇飛的經典程序。
此外,要想在移動無線系統中成功的使用Turbo碼,首先要考慮在語音傳輸中最大延遲的限制。在短幀情況下的模擬結果表明短交織Turbo碼在AWGN通道和Rayleigh衰落下仍然具有接近通道容量的糾錯能力,從而顯示出Turbo碼在移動無線通信系統中非常廣闊的應用前景。
Turbo碼(Turbo Code)
Turbo 碼(Turbo Code)是一類應用在外層空間衛星通信和設計者尋找完成最大信息傳輸通過一個限制帶寬通信鏈路在數據破壞的雜訊面前的其它無線通信應用程序的高性能糾錯碼。有兩類 Turbo 碼在那裡,塊 Turbo 碼和卷積 Turbo 碼(CTCs),它們是相當不同的,因為它們使用不同的構件碼,不同的串聯方案和不同的 SISO 演演算法。
在E-UTRA系統中,Turbo碼速率匹配原理如圖3-38所示,也採用CBRM的速率匹配方式。在圖3-38中,Turbo編碼器輸出的系統比特流、第一校驗比特流和第二校驗比特流分別獨立地交織后,被比特收集單元依次收集。首先,交織后的系統比特流依次輸入到緩衝器中,然後交織后的第一校驗比特流和第二校驗比特流交替地輸入到緩衝器中。
在TD-LTE物理層,HARQ重傳規定了4個冗餘版本(RV,Redundancy Version),因此CBRM對於同一個編碼數據塊對應著4個傳輸開始的比特位置。這4個冗餘版本均勻地分佈在緩衝器中,以快速地發起重傳。根據高層配置的冗餘版本,從冗餘版本對應的比特開始,比特選擇單元從緩衝器中逐位讀取,直至達到預定的比特數。當讀取到緩衝器的尾部,仍然沒有達到預定的比特數時,比特選擇單元自動跳至緩衝器的頭部繼續讀取。
Turbo碼速率匹配採用的交織器與卷積碼相同,不再累述。
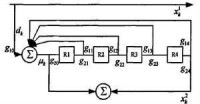
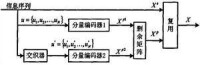
Turbo 碼最先是由C. Beηou等提出的。它實際上是一種并行級聯卷積碼(Parallel Concatenated Convolutional Codes)。Turbo 碼編碼器是由兩個反饋的系統卷積編碼器通過一個交織器并行連接而成,編碼后的校驗位經過刪余陣,從而產生不同的碼率的碼字。如圖所示:信息序列經過交織器形成一個新序列(長度與內容沒變,但比特位經過重新排列),u 和u'分別傳送到兩個分量編碼器(RSC1與RSC2) ,一般情況下,這兩個分量編碼器結構相同,生成序列X和X,為了提高碼率,序列X和X需要經過刪余器,採用刪余(puncturing)技術從這兩個校驗序列中周期的刪除一些校驗位,形成校驗序列X,X,與未編碼序列X'經過復用調製后,生成了Turbo碼序列X.
Turbo 碼的一個重要特點是它的分量碼採用遞歸系統卷積碼(RSC,Recursive Systematic Convolutional code) ,這也是它性能優越的一個重要原因。之所以選擇RSC編碼器作為Turbo碼的子碼主要有以下原因:
首先,RSC碼具有系統碼的優點。這一特性使用戶在解碼時無需變換碼字而直接對接收的碼字進行解碼,所以,遞歸系統卷積碼(RSC)對於非系統卷積碼(NSC)而言解碼簡單、快速。
其次,從差錯控制編碼的相關文獻中可知,非系統卷積碼(NSC)的BER性能在高信噪比時比約束長度相同的非遞歸系統碼要好,而在低信噪比時情況卻正好相反。遞歸系統卷積碼綜合了NSC碼和非遞歸系統卷積碼的特性,且然它與NSC碼具有相同的trellis結構和自由距離,但是在高碼率的情況下,對任何信噪比,它的性能均比等效的NSC碼要好。由於系統遞歸卷積碼具有以上特點,並且能改善誤碼率,所以通常選擇RSC碼作為Turbo碼的子編碼器。
式中,1表示系統比特,gl 和g2分別表示編碼器的前饋多項式和反饋多項式。用RSC碼構成Turbo碼的分量碼的碼率R為:
式中:R1,R2為構成Turbo 碼的分量碼的碼率,在經刪余后,分量RSC1和RSC2的碼率可以不同。
Turbo 碼的最大似然解碼性能分析出,Turbo 碼在高信噪比下的性能主要由它的自由距離所決定。因為Turbo碼的自由距離主要由重量為2的輸入信息序列所產生的碼字間的最小距離所決定,用本原多項式作為反饋連接多項式的分量編碼器所產生的碼字的最小重量為最大,因此當Turbo碼交織器的大小給定后,如果分量碼的反饋連接多項式採用本原多項式,則Turbo碼的自由距離會增加,從而Turbo碼在高斯信噪比情況下的“錯誤平層(errorfloor)”會降低。錯誤平層效應指的是在中高信噪比情況下,誤碼曲線變平。也就是說,即使是再增大信噪比,無碼率也降不下來(一般的系統,比如說是BPSK的誤碼曲線,誤碼率隨著信噪比的增大是單調下降的)。
交織器是影響Turbo碼性能的一個關鍵因素,它可以便Turbo碼的距離譜細化,即碼重分佈更為集中。它的特性的好壞直接關係著Turbo碼的性能。
編碼器中交織器的使用是實現Turbo碼近似隨機編碼的關鍵。交織器實際上是一個一一映射函數,作用是將輸入信息序列中的比特位置進行重置,以減小分量編碼器輸出校驗序列的相關性和提高碼重。通常在輸入信息序列較長時可以採用近似隨機的映射方式,相應的交織器稱為偽隨機交織器。由於在具體的通信系統中採用Turbo碼時交織器必須具有固定的結構,同時是基於信息序列的,因此在一定條件下可以把Turbo碼看成一類特殊的分組碼來簡化分析。交織是對信息序列加以重新排列的一個過程。如果定義一個集合A ,。則交織器可以定義為一個一一對應的映射函數π(i),(i,j屬於A) 這裡的i ,j 分別是未交織序列C 和交織序列C' 中的元素標號。映射函數可以表示為。其原理如圖 在交織器的設計中,基本上是遵循下列原則:
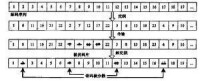
Turbo碼
3) 儘可能避免與同一信息位直接相關的兩個分量編碼器中的校驗位均被刪除;
4) 對於不歸零的編碼器,交織器設計時要避兔出現"尾效應" 圖案。
在設計交織器時,應考慮具體應用系統的數據的大小,使交織深度在滿足時延要求的前提下,與數據大小一致,或是數據幀長度的整數倍。
交織器和分量碼的結合可以確保Turbo碼編碼輸出碼字都具有較高的漢明重量。在Turbo編碼器中交織器的作用是將信息序列中的比特順序重置。當信息序列經過第一個分量編碼器后輸出的碼字重量較低時,交織器可以使交織后的信息序列經過第二個分量編碼器編碼后以很大的概率輸出較高重碼字,從而提高碼字的漢明重量:同時好的交織器還可以奇效地降低校驗序列間的相關性。因此,交織器設計的好壞在很大程度上影響著Turbo碼的性能。
交織器的類型可以分為兩大類,一是規則交織器,也稱確定性交織器,其交織器的映射函數可以由一個確定的解析函數給出。二是隨機交織器,其映射函數不能由-個確定的解析表達式給出。
Turbo 碼常用的交織器包括以下幾種:分組交織器、隨機交織器、s-隨機交織器等等。
對於數字通信領域日益緊張的帶寬資源,提高碼率就意味著節省帶寬和降低通信費用。刪余(Puncturing)是目前提高Turbo碼碼率的主要方法。
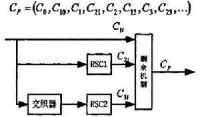
Turbo碼
Turbo 碼中,刪余器通常比較簡單,因為在一般的應用中,碼率都是在 或者 ,因此即使有刪余器,它一般也只是周期性的從兩個分量編碼器中選擇校驗比特輸出即可。其具體做法是:從兩個RSC編碼生成的校驗序列中周期地刪除一些校驗位,然後再與未編碼的信息序列復用重組成最後的編碼輸出序列,調製後進入通道傳輸。若信息序列為 ,長度為N ,那麼兩個RSC分量編碼器的輸出為:圖3. 6 所示示為採用了刪余技術的編碼結構,若取RSC1輸出的奇比特和RSC2的偶比特,即採用刪余矩陣 ,那麼編碼輸出長度為2N,碼率提高為的序列為Cp. 兩個分量碼編碼器的輸出經過刪余得到的序列被稱為奇偶序列,是校驗序列。一個好的刪余演演算法應該符合以下幾點要求:
1) 不能刪除信息位。刪除信息位會造成較大的信息損失,從而使誤碼率有較大的損失;
2) 刪余應該在時間域上均勻進行,刪余同一時刻所有的比特位會造成此時刻信息損失較大,影響誤碼率;
3) 刪余應該對於各分量碼均勻進行,從而使信息的損失均勻分佈在各分量碼上,避免由於信息損失不均勻導致分量碼解碼性能下降。
典型的Turbo碼編碼器由兩個遞歸系統卷積碼(RSC,Recursive Systematic Convolutional codes)并行級聯而成,因此Turbo碼又被稱為并行級聯卷積碼(PCC,Parallel Concatenated Convolutional codes)。
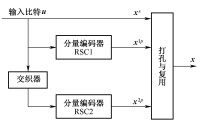
圖3-33 Turbo碼編碼器的結構
Turbo碼編碼器一般包括兩個結構相同的遞歸系統卷積編碼器和一個隨機交織器。長度為 N的信息序列 u一方面直接進入第1個分量編碼器RSC1,另一方面經過隨機交織器處理後送入第2個分量編碼器RSC2。隨機交織器的處理是輸入序號至輸出序號的一映射,它的輸出為長度相同,但比特位置經隨機排列的交織序列。兩個分量編碼器RSC1和RSC2分別產生兩個不同的校驗比特序列 x和 x。為了提高Turbo碼的碼率,除可以選用高碼率的分量碼外,還可以採用打孔(Puncturing)技術從這兩個校驗序列中刪除一些校驗位,然後再與信息序列 x 復用在一起輸出。例如,假定圖3-33中兩個分量編碼器的碼率均是,為了得到碼率的Turbo碼,可以採用打孔矩陣,即刪去來自RSC1的校驗序列 x的偶數位置比特與來自RSC2的校驗序列 x的奇數位置比特。為了處理更加簡單,在TD-LTE中採用了循環緩存速率匹配技術(CBRM,Circular Buffer Rate Matching),具體內容見3.5.2.2節相關描述。
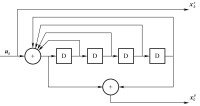
圖3-34 (37,21)分量編碼器RSC結構
Turbo碼的解碼複雜度一般隨分量編碼器的寄存器個數呈現指數級增長。例如,(37,21)Turbo碼使用4個寄存器,解碼複雜度一般是16的倍數。在TD-LTE系統中,Turbo的分量編碼器的生成多項式為,使用了3個寄存器,因此解碼複雜度較小。
Turbo碼內置的交織器是在第2個分量編碼器RSC2編碼處理之前將信息序列的 N個比特的位置進行隨機排列,它起著關鍵的作用,很大程度上影響著Turbo碼的性能。通過隨機交織,使得編碼由簡單的短碼得到了近似長碼。當交織器充分大時,Turbo碼就具有近似於隨機長碼的特性。
在E-UTRA系統中,Turbo碼的交織器採用二次置換多項式函數(QPP,Quadratic Permutation Polynomials),即
Turbo碼
Turbo碼解碼器採用迭代解碼方法,其中使用兩個分量解碼器,並在第一分量解碼器與第二分量解碼器之間傳遞軟解碼信息,如圖3-35所示。無衝突交織器支持并行解碼的主要原理是:在進行迭代解碼時,第一分量解碼器將信息序列進行分段,每個分段使用單獨的一個專用的解碼處理單元獨立地進行解碼,各分段解碼過程可以并行進行,提高解碼速度。但是第二分量解碼器也需要採用相同的、并行的分段解碼方法,這就要求第二分量解碼器的每個獨立專用的解碼處理單元同一時刻訪問不同的分段,這樣才能避免信息序列分段地訪問衝突,從而實現第二分量解碼器的并行分段解碼,提高整個迭代解碼的速度。圖3-36所示為無衝突交織器的示意圖,4個窗口(Windows)A、B、C、D分別代表獨立的分段解碼,它們需要通過交織器獲取各自的原始數據,此時4個窗口A、B、C、D在讀取原始數據時,不會出現在同一時刻訪問同一分段,不會發生資源訪問衝突的問題,這樣保證了4個窗口A、B、C、D可以并行地分段解碼。
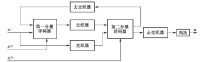
圖3-35 Turbo碼解碼器的迭代解碼框圖
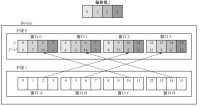
圖3-36 并行解碼示意圖
為了支持靈活的系統結構,同時保證魯棒的系統性能,在TD-LTE系統中優化設計了188種QPP交織器長度,可以支持相應的188種Turbo編碼塊大小。這裡,列舉其中的3種交織器。
例1:當 N=40時,則。
例2:當 N=1008時,則 ,。
例3:當 N=6144時,則,。
TD-LTE Turbo碼的QPP交織器長度 N的每個因子都可以作為分段大小和并行度,比如例3中,,對應的Turbo解碼器可以使用8個并行的分段解碼器,每個分段解碼器的解碼長度是768bit。
QPP交織器除了支持并行解碼,還有其他的優點,例如計算複雜度較小,實現非常簡單等,因此被應用於TD-LTE系統中。
為了便於分析Turbo碼的理論性能的上界(Upper Bound),一般使用誤比特率(BER)來統計性能,並假設最大似然解碼(ML)、BPSK調製和加性高斯白雜訊通道(AWGN)。Turbo碼的性能上界就可以使用聯合界(Union Bound)來確定,即
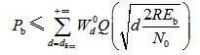
Turbo碼
其中,是首一輸入序列對應的所有重量為 的碼字中信息位的全部重量之和。
式(3-19)還可以進一步寫成
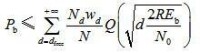
Turbo碼
其中, 代表碼字重量為 d的每個碼字的平均信息位重量,代表碼字重量為 d的碼字數目,即碼字多樣性(Multiplicity)。另外,還定義一個等效的多樣性(Effective Multiplicity),即
Turbo碼
當信噪比較高時,式(3-20)可以進一步簡化,獲得Turbo碼的漸近性能(Asymptotic Performance),即
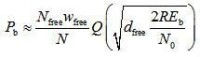
Turbo碼
式(3-22)說明,Turbo碼的漸近性能主要是由自由距離()決定的。
為了進一步解釋Turbo的性能界,以上述(37,21)Turbo碼為例,交織器大小為65536,它的碼率,自由距離 ,平均重量 ,等效的多樣性為
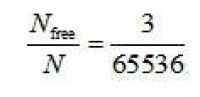
Turbo碼
Turbo碼的漸近性能為
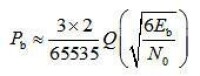
Turbo碼
圖3-37給出了這個式(3-24)對應的漸近性能曲線,同時給出了(2,1,14)卷積碼的漸近性能曲線作為對比。Turbo碼性能界出現的平坦特徵主要由較小的自由距離決定,而卷積碼的性能界出現陡峭特徵主要由較大的自由距離決定。Turbo碼的性能優勢主要出現在較低的信噪比範圍,此時漸近性能曲線位置相對較低,其原因是Turbo碼具有很小的等效多樣性,這在很大程度上決定了Turbo碼的優異性能。顯然,交織器長度越大,對應的信息比特長度 N越大,Turbo碼的性能增益就越大。
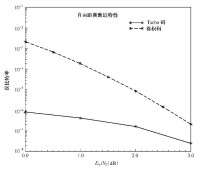
圖3-37 Turbo碼性能界
香農資訊理論告訴我們,最優的解碼演演算法是概率解碼演演算法,也就是最大后驗概率演演算法(MAP)。但在Turbo碼出現之前,通道編碼使用的概率解碼演演算法是最大似然演演算法(ML)。ML演演算法是MAP演演算法的簡化,即假設信源符號等概率出現,因此是次優的解碼演演算法。Turbo碼的解碼演演算法採用了MAP演演算法,在解碼的結構上又做了改進,再次引入反饋的概念,取得了性能和複雜度之間的折衷。同時,Turbo 碼的解碼採用的是迭代解碼,這與經典的代數解碼是完全不同的。
Turbo碼
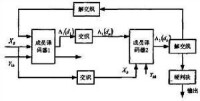
⒈Turbo 碼的解碼結構如圖所示. Turbo 解碼器有以下的特點:
1) 串列級聯
2) 迭代解碼
3) 在迭代解碼過程中交換的是外部信息
⒉ 概率解碼解碼原理及結構
解碼時首先對接收信息進行處理,兩個成員解碼器之間外部信息的傳遞就形成了一個循環迭代的結構。由於外部信息的作用,一定信噪比下的誤比特率將隨著循環次數的增加而降低。但同時外部信息與接受序列間的相關性也隨著解碼次數的增加而逐漸增加,外部信息所提供的糾錯能力也隨之減弱,在一定的循環次數之後,解碼性能將不再提高。
Turbo碼
是對bahl軟輸出演演算法做一定修正後,通過除以先驗分佈來消除正反饋的演演算法。對於約束長度為M 1的卷積碼,其運算量為每比特次乘法和次加法。由於乘法運算量大,限制了解碼的規模和速度。
實際上就是對標準MAP演演算法中的似然全部用對數似然度來表示,這樣,乘法運算變成了加法運算。總的運算量成為次加法,次求最大運算和次查表。
是在上述對數域的演演算法中,將似然值加法表示式中的對數分量忽略,是似然加法完全變成求最大值運算,這樣除了省去大部分的加法運算外,最大的好處是省去了對信噪比的估計,使得演演算法更穩健。
Turbo碼
目前Turbo 碼的大部分研究致力於在獲得次優性能的情況下減小解碼複雜度和時延,從而得到可實現的Turbo碼系統。
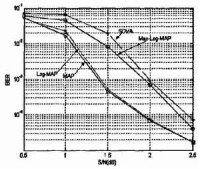
1.幾種主要解碼演演算法的性能比較
Turbo碼
對MAP演演算法、Log-MAP演演算法、Max-Log-MAP演演算法和SOVA演演算法在加性高斯白雜訊通道(AWGN)環境下進行模擬比較,系統採用的是BPSK調製方式,Turbo 碼的交織長度是1024 , RSC子碼的生成多項式為(37,21) ,系統編碼率為,解碼時迭代5次,結果以曲線圖給出如圖。模擬結果表明,四種演演算法中,MAP演演算法性能最好,Log-MAP 演演算法的性能跟MAP 演演算法在較低的SNRq時比較接近,高信噪比時差別則較大。Max-Log-MAP演演算法和SOVA演演算法的性能十分接近,一般情況下,Max-Log-MAP演演算法的性能,總是稍優於SOVA演演算法。它們跟MAP和Log-MAP相比,性能下降十分明顯。從演演算法複雜度而言,MAP演演算法最為複雜,Log-MAP 其次,之後是Max- Log-MAP ,SOVA演演算法最簡單。由此可以看出,性能優異的Turbo碼解碼演演算法十分複雜,如果要使得解碼容易實現而對演演算法進行簡化或者是採用簡單的演演算法,往往需以性能的降低為代價。
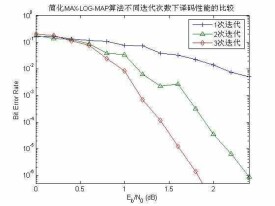
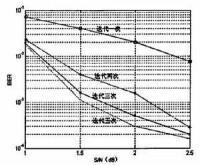
⒉ 不同迭代次數對Turbo碼性能的影響
迭代次數對Turbo碼的影響 左圖給出了在不同解碼迭代次數下,碼率為的Turbo碼的BER與的關係曲線。Turbo 碼的交織長度是1024 ,RSC 子碼的生成多項式為(37,21) ,系統編碼率為。如Turbo碼解碼原理中所述,兩個解碼器之間互相交外部信息進行迭代。可以得到,迭代解碼次數增大,解碼性能增加。在第一次迭代的誤比特性能都比較差,這是因為兩個分量解碼器之間的信息還沒有被很好的相互利用。隨著迭代次數的增加,兩個分量解碼器之間的外信息被更好的利用,對信息比特的估計更接近最大似然比,判決輸出的正確性就越高。迭代次數達到一定數值時,解碼性能趨於穩定,再增加新的迭代對性能的改善非常小。迭代增加了解碼時延,在大幀編碼時尤其如此。模擬中迭代次數增大時運行時間顯著增加。
由於達到一定迭代次數后,新增加的迭代對性能改善不大,而法代又極大地增加解碼時延,所以在實際設計Turbo碼系統時,需要選擇適當的迭代次數,在允許的解碼時延內,達到最佳的解碼性能。這種預先規定迭代次數的方式是終止解碼迭代次數的方法之一。當要求的信噪比比較大,誤碼率要求不太高的情況,往往經過很少的幾次迭代就能達到解碼要求正確解碼。此時,如果預設迭代次數比較大,那麼解碼器會繼續解碼,一直進行到預設次數的迭代為止。後邊的幾次送代並沒有明顯地提高性能,是完全不必要的,而且多餘的法代食給解碼帶來了額外的時延。
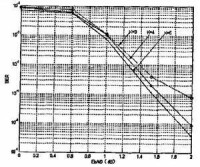
⒊ 不同編碼約束度K 對Turbo 碼性能的影響
不同的約束度對Turbo 碼性能的影響
採用不同子碼的Turbo碼的性能也有很大差別。Turbo 碼的設計中首先就是選擇好的RSC子碼。這裡只對幾種常用的、較好的採用不同約束長度的RSC 做子碼的Turbo 碼進行模擬,以分析約束長度對Turbo 碼性能的影響。可以看出,隨著約束長度K增大,編碼后的碼元與更多個信息比特相關,因此解碼糾錯能力越強誤比特率HER就越小。當BER<10-2e 時,增加卷積碼的約束度將會改善Turbo 碼HER性能。在交織器長度和碼率一定時,約束度越大,Turbo 碼的HER 性能越好。
通道編碼技術可改善數字信息在傳輸過程中雜訊和干擾造成的誤差,提高系統可靠性。因而挺供高效的通道編解碼技術成為3G移動通信系統中的關鍵技術之一。3G移動通信系統所提供的業務種類的多樣性、靈活性,對差錯控制編解碼提出了更高的要求。WCDMA 和cdma2000方案都建議採用除與IS-95 CDMA系統類似的卷積編碼技術和交織技術之外,採用Turbo編碼技術。
⒈ RSC 編碼器的設計
cdma2000 方案中,Turbo 碼被用在CDMA系統前向、反向鏈路通道中。反向鏈路通道中,子編碼器(3,1,3)RSC 的生成矩陣為:
Turbo碼
RSC編碼器基於8狀態的并行級聯卷積碼(8PCCC)。交織採用了比特翻轉技術。通過刪余處理,碼率為,,的Turbo碼被採用。分別對兩個子編碼器的輸出奇偶位V2和V2‘交替刪余,可得到碼率為的Turbo碼;對V1,V1' 刪余,可得碼率為;對V2、V2’間隔幾V1,V1‘刪余,可得碼率1/2。
WCDMA中,對於收務服務質量需求BER介於10-3e和10-6e之間。並且允許時延較長的數據業務,RSC子編碼器使用8態并行級聯卷積碼8-PCCι。生成矩陣為:
WCDMA中的turbo編碼器
⒉ 交織長度的選擇
在3G移動通信中,業務速率由32kbit/s到2Mbit/s。10ms一幀,幀長由20 到20000。為了提高解碼器性能,在一些低速業務中,可採用多幀組成一個數據塊,加大交織深度。
在WCDMA中,Turbo 碼交織器是可截短型塊交織器。交織行數為5、10或20行,在行數確定的基礎上選擇列數。數據按行讀入交織器,按固定模式進行行間轉換,不同輸入序列長度對應不同的行數和行間轉換模式。行轉換完成後,近行列轉換。不同行對應不同列間轉換參數,採取的是接近隨機化的素數取模演演算法。數據在完成行列轉換后,按列讀出。
cdma2000 也是基於塊交織。交織行數為行,列數N=2n,n為滿足使32N大於或等於幀長度的最小值。數據按行讀人。行間轉換的依據是比特翻轉原則。列問轉換的置換公式是:,即為同模取余法,為了更接近隨機化,使每列的偏置取不同值。數據經過行列轉換后,按列輸出。
⒊ 解碼器的設計
由於Turbo碼解碼演演算法複雜,解碼延時長,所以對於時延要求高的數據業務應用受限。因而低複雜度解碼器的設計成為Turbo碼解碼演演算法設計的焦點。為了換取複雜度的簡化,允許次優性能解碼的存在。例如3GPP中允許Turbo碼的譯間比標準MAP演演算法有1dB的增益損失。結合CRC校驗來減少迭代次數,在SNR 較大時可以減少解碼複雜度和解碼延時。
日前Turbo碼的研究尚缺少理論基礎支持,但是在各種惡劣條件下(即低SNR情況下),提供接近Shannon 極限的通信能力已經通過模擬證明。但Turbo碼也存在著一些急待解決的問題,例如解碼演演算法的改進、複雜性的降低、解碼延時的減小。作為商用3G 移動通信系統的關鍵技術之一,Turbo 碼也將逐漸獲得較好的理論支持並且得到進一步開發和完善。