金屬電子論

研究金屬中電子運動狀態的理論。金屬由一種或多種元素的原子所組成。晶體學和金屬學從原子尺度研究金屬，而電子論則從電子的運動狀態闡述金屬的結構與特性。當孤立的原子結合成金屬時，各原子的原子核和內層電子所構成的離子實變化很少，而外層電子的運動狀態則顯著改變。金屬中帶正電的離子實組成周期排列的空間點陣，而帶負電的外層電子則由原來被束縛在單個原子內的局域狀態變為整個點陣所共有的狀態。因此，這些電子可以起到導電、導熱作用，稱為傳導電子或自由電子。傳導電子的公有化是金屬鍵的主要特點。

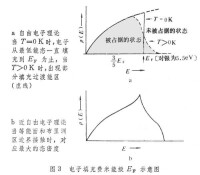
電子論闡述;①單個電子在金屬中受到的作用力，以及在其作用下電子的運動狀態；②金屬中數量極大，本質上相同的電子在不同的能量狀態中的分佈；③在前二者的基礎上對電子進行統計研究，獲得有關的宏觀性質。

金屬中的傳導電子，既受到所有離子實的作用，也受其他眾多的傳導電子的作用。

早期的經典電子論，把金屬中的傳導電子作為在金屬內部自由運動的經典粒子。除碰撞外不受點陣離子實的作用。它們相當於容器中自由運動的理想氣體的分子（因而稱為自由電子氣），電子的能量是可以連續變化的，自由電子氣服從玻耳茲曼（Boltzmann）分佈律。

量子力學建立之後，用以處理自由電子運動，並採用量子統計，使自由電子論得到了發展。後來又用周期場來反映離子實點陣的作用，得到了能帶理論。

在具有周期起伏勢場的離子實點陣中，在相鄰兩陣點間的中點附近，場強接近於零；但在離子實中心附近，電子受到很強的吸引力，處理這問題可以有不同的近似方法。

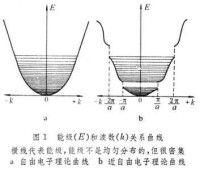
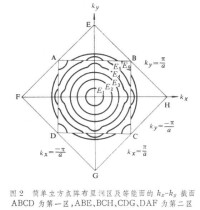
近自由電子理論 以自由電子狀態作為起點，考慮一個微小起伏的周期勢場的影響，用微擾法解薛定諤方程。圖 1b是一維情況下的主要結果（圖 1是自由電子論中自由能級和波數的關係曲線）。對於大多數能級，電子和自由電子相似曲線仍為拋物線,E為電子能量，k為電子波數。曲線在某處(a為點陣周期,n為整數）附近，曲線發生間斷，出現能隙，曲線偏離原來的拋物線。准連續的能級分成一些能帶，電子不能具有能隙內能級的能量（即禁帶），能隙寬度決定於周期勢場相應的傅里葉分量，因而與該方向上的點陣周期和勢函數的形式有關。出現間斷的條件相當於電子波在相應晶面反射的布喇格條件（d為晶面間距,θ為入射波與晶面的夾角）。

三維晶體中的能隙用布里淵區描述。布里淵區是按照金屬點陣周期性在空間中劃出的區域，即由原點和倒易陣點聯線的垂直平分面劃出的。例如對一個簡單立方點陣，其三維倒易點陣在方向的周期均為，原點為中心，由、、六個平麵包圍的立方體即第一布里淵區。由更遠的陣點可構成第二、第三……等區。圖2 畫出第一、二兩區的截面。每個方向上的關係具有圖1b的特徵，可以將三維空間等能面的截面同時表示於圖2中。遠離布里淵區邊界的等能面保持自由電子的球面，接近區界發生偏離。隨的增加，能量增加逐漸變緩，等能面向外突出，但不能穿過區界。和自由電子論對照，能帶理論的一個能區的(態密度即在電子能量E與之間具有的能級數)與E的關係曲線如圖3所示。在初始階段接近拋物面，當等能面與布里淵邊界接觸時對應最大的態密度，此後繼續提高能量只有布里淵區角上的狀態可以填充，因此愈來愈少。簡單立方晶體各布里淵區的體積均為，除以每個量子態所佔的體積，得出一個區含有個狀態（N為金屬所含原子數）。電子按照費密-狄喇克分佈律每個能級只能有兩個電子，從低能態到高能態填充布里淵區。能區僅部分填充的，例如一價金屬共有N個電子，只填充一半，則形成導體，因為能區中尚有大量空態，電子可以從外加電場獲得微小附加動能向上躍遷而導電。若電子數正好填滿能區，例如則可能有兩種情況：由於三維空間中，各方向的能隙大小可能不同，如兩個區所對應的上、下能帶之間有禁帶相隔，即第一區各方向的最高能級均低於第二區的最低能級，則成為絕緣體；如兩個能帶相互重迭，即第一區有些方向的最高能級比第二區某些方向的最低能級高, 此時電子在第一區未填滿時就開始填充第二區，因而也可成為導體，如二價的金屬；若低能帶雖已填滿，但禁帶窄，滿帶頂部的電子可吸收能量而躍遷到上面的空帶，變成傳導電子，同時滿帶缺失電子的空態也可在外場作用下轉移，產生空穴導電性。本徵半導體屬於這個類型。也可能由於雜質產生傳導電子和空穴，如摻雜半導體。

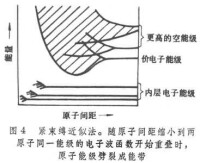
緊束縛近似法 以電子被束縛在各孤立原子的狀態為起點，考慮結合成金屬后近鄰原子的相互作用。設想兩原子相互接近，當原子間距縮小到兩原子同一能級的電子波函數開始重疊時，該能級便分裂為二，裂距隨原子間距的縮小而變大。類似地,N個原子結合成固體時，一個原子能級分裂成N個次能級，對應著N個單原子波函數不同線性疊加而組成波函數，這N個次能級形成一個準連續的能帶，可容納個電子。圖4表示隨著原子間距的縮小，原子能級劈裂成能帶的情況。距離愈近，能帶愈展寬。但不同能級受影響程度不同，最先分裂的是價電子能級，內層電子能級只在原子非常接近時才分裂。緊束縛法直接將孤立原子能級和能帶聯繫起來，因此和近自由電子法可以互為補充。但由於起點不同，其結果的適用性不同，近自由電子論較適於接近自由的傳導電子，例如鹼金屬價電子，緊束縛法則對於比較局限於所屬原子附近的電子較為適用。

其他方法 上面方法(例如過渡族金屬的d電子),均系採用單電子近似，沒有考慮電子之間的交互作用，更精確的理論要求計入電子的相互關聯。除此以外，還有元胞法，正交平面波法及贗勢法等方法，其目的都是為了使計算更精確、更符合實際。

參考書目

黃昆:《固體物理學》,人民教育出版社，北京，1966。

J. Callaway, Energy Band Theory,Academic Press,New York,1964.

D.F.Gibbons.Electron Theory of Metals，in R.W.Cahn ed.,Physical Metallurgy,2nd rev.ed.,pp.71～158,North-Holland,Amsterdam,1970.

W.A. Harrison: Electronic Structure and the Properties of Solids.Freeman,New York,1980.