偽隨機序列
偽隨機序列
偽隨機序列,是指如果一個序列,一方面它是可以預先確定的,並且是可以重複地生產和複製的;一方面它又具有某種隨機序列的隨機特性(即統計特性),我們便稱這種序列為偽隨機序列。
目錄
序列元素間有確定關係存在,但具有與隨機序列類似性質的一種特殊的離散信號形式,可表示為
其中可取值0,1或1,-1;也可以取符號域(見分組碼)中的元素。前者叫二元序列,後者叫 q元序列。但實用中最主要的還是前者。序列長度可以為有限,也可以為無窮。後者主要著重的是周期序列,即存在最小正整數夞,使對一切i有,p為周期。
序列的各元素為相互獨立且具有相同分佈的隨機變數時,稱為隨機序列。實際應用的主要是偽隨機序列。它指序列元素間有確定關係存在,但具有與隨機序列類似的下列性質:①在有限長度或一周期內各元素的個數相差不超過1,即接近等概率;②出現 l個相同值或稱l長遊程的概率接近;③相關函數 (1)
在時為厵0時不超過,式中為序列的長度或周期。實際上有時將大體滿足以上條件的序列也稱為偽隨機序列。
發展概況 相關函數接近衝激函數的信號是相關檢測系統中比較理想的形式。為了構造這樣的信號,1953年R.H.巴克首先找到長度為有限的一些二元序列具有上述特點,稱之為巴克序列。可惜,已知的巴克序列最大長度為13,且已證明不存在比13更長的奇長巴克序列,對於偶長巴克序列長度應為,已證明的序列也不存在,故難以滿足要求較高的場合。為了獲得長度較長、性能較好且數量較多的序列,理論上較易解決的是可用反饋移位寄存器實現的無限周期序列。這主要有M序列和L序列等,前者為線性移位寄存器序列,後者為非線性移位寄存器序列。
序列的構造 偽隨機序列可用圖中 ɑ的反饋移位寄存器得到。圖中表示反饋函數。n 級移位寄存器只能有(一般為)種狀態, 故經一定時間後會回到原來的某一狀態, 產生周期性輸出, 若反饋函數的輸出與各輸入,…,間有線性關係存在,則為線性移位寄存器,否則為非線性移位寄存器。圖中b和c分別是三級線性和非線性反饋移位寄存器。
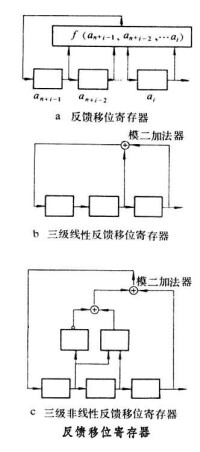
偽隨機序列
(2)
它當初始值全為零時輸出恆為零。除去這種全零狀態外,它最多可能取遍所有個非零狀態,故最大周期為 。一般情況下周期是 的因子。
周期達到的序列稱為最長線性移位寄存器序列,簡稱M序列,圖中b就是三級M序列,它的輸出為…,0,0,1,0,1,1,1,…。M序列完全滿足偽隨機序列的三點要求,特別是它的相關函數為
(3)
因而是典型的偽隨機序列。
M序列的周期一定是 ,實用上還需要有其他的周期,這可用非線性移位寄存器序列得到。n級非線性移位寄存器序列的周期不大於,達到的序列稱M序列。
一般M序列的相關函數不完全接近衝激函數。接近衝激函數的非線性移位寄存器序列主要有二次剩餘或稱勒讓德序列,簡稱L序列,以及孿生素數序列。兩者的相關函數均如式(3)。L序列是周期為形如的素數時所構造的序列,k為自然數。前幾個L序列的周期為3,7,11,19,23,…。當周期不超過任一大的正整數時,L序列的種類比M序列多得多。孿生素數序列是周期為的偽隨機序列,在此k與均為素數,前幾個序列的周期為15,35,143,…。
偽隨機序列族 應用中有關的全部序列叫序列族,且通常取周期相同的一族序列。既有良好的自相關特性又有良好的互相關特性的線性偽隨機序列族,主要有戈爾德序列族和嵩忠雄序列族等。
戈爾德序列族是由適當選擇的一對n級M序列線性組合構成,在此n呏1(mod 4)或n呏2(mod 4)。序列族中共有個序列,周期均為,兩兩之間的互相關函數最大值為,此處表示不超過x的最大整數。n為偶數時戈爾德序列的性能較差,而嵩忠雄序列卻可達到最佳。後者由n級M序列和相應的級M序列的線性組合構成。它的周期也是 ,但序列只有個,互相關函數最大值是。
應用 偽隨機序列作為一種信號形式,具有良好的相關特性,可作為雷達測距、同步和線性系統測量的信號。它還具有偽隨機性,因而可用於加密系統和偽隨機跳頻等場合。這時常將序列經非線性變換,即構造前饋序列;或者用多個序列組合后輸出以增加保密性。它還可用以產生偽隨機數適於計算機的系統模擬和在數字系統中作為誤碼測試信號等。偽隨機序列還可用於擴頻,在多址系統中作為地址信號等。偽隨機序列有多方面的應用,對它的要求也很不相同。例如用於多址信號時不但要求它通常的互相關函數要小,而且和在中間任意一位處反相后的互相關函數也要小;又如用於加密系統時,不但要考慮它的分析,而且要考慮它的綜合和計算複雜性。關於非線性移位寄存器序列,尚有許多問題沒有完全解決。
參考書目
S.W.Golomb, Shift Register Sequences,Holden-Day, San Francisco,1967.