共找到2條詞條名為臨界現象的結果 展開
- 臨界現象
- 相變理論
臨界現象
臨界現象
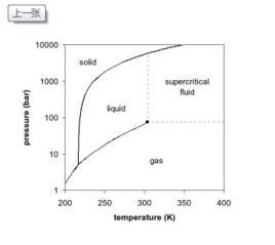
臨界現象(critical phenomenon)是指物質處在臨界狀態及其附近具有的特殊的物理性質和現象。1869年T.安德魯斯研究二氧化碳氣、液兩相 密度差時發現,溫度在31.04℃時氣、液密度趨同,兩相界限消失,取名為臨界狀態。
1871年J.范德瓦耳斯提出真實氣體狀態方程,方程中引入氣體分子本身的體積,分子間吸引力所減輕的氣體對容器壁的壓力 / ,方程的形式為:
式中p是氣體壓力,V是氣體體積,R是氣體常數,T為氣體絕對溫度。方程指出了氣體在一定壓力、溫度下可以液化。其中參數a和b與氣體的臨界參數p、T和V有關:
,
如果壓力、溫度、體積以臨界點參數作為單位,即、、,則范德瓦耳斯方程可寫成:
它不包含任何錶征特定物質的量,適用於任何物質的氣態和液態。這是最早提出的平均場的普適狀態方程。
1907年P.外斯提出用分子場理論解釋鐵磁性,這是一種描述特殊相變的平均場理論。1937年L.朗道提出用序參量描述相變形式的理論,特別是他與V.京茨堡建立的超導唯象波函數理論。1945—1965年大量精確的實驗測量證實,在臨界點附近物質特性的物理量與溫度 之間的關係均可寫成,稱為臨界指數。這些指數與平均場理論不符。1966年L.卡達諾夫指出標度概念的重要性,在臨界點附近粒子之間的關聯、漲落起重要作用。1971年K.威耳孫用量子場論中重正化群方法,對卡達諾夫的物理概念進行了數學表述,論證了實驗上總結出的臨界現象的標度律和普適性,計算出符合實驗的臨界指數。威耳孫為此獲得了1982年諾貝爾物理學獎。
冰化為水,水變成水蒸氣都需要吸熱,相反的過程伴隨放出熱量,這是一級相變。在相變點兩相的化學勢相等,但化學勢的一級偏導數代表的物性有突變。二級相變又稱連續相變,物質兩相的化學勢及其一級偏導數相等,但二級偏導數有突變。固體中居里點的鐵磁-順磁相變、在沒有外磁場時金屬正常態-超導態相變都是二級相變。
連續相變時體系的對稱性往往發生改變,處在高溫相的對稱性高,處在低溫相的對稱性低。朗道用序參量描述這兩相的差異,高溫相的序參量,低溫相的序參量。在氣-液臨界點的相變中序參量ψ可選為兩相密度差ρ-ρ,或比容差v-v,式中l、g分別代表液相和氣相,ψ為實數。對於金屬正常態-超導態的相變,序參量為超導電子有效波函數,代表超導電子密度,是複數。朗道認為系統的自由能F在相變點附近可用序參量展開成冪函數:
由自由能極小條件給出ψ的平衡值。對於氣-液臨界點相變,ψ是實數。通常取參數 ,,這裡a和b都是常數,於是由,得:
,當
,當
ψ代表液體密度ρ與氣體密度ρ之差。所以,臨界指數。
在臨界點附近,序參量相對於平衡值有大的漲落,通常用r=0和r兩點之間的關聯函數來表示:
〈 〉表示統計平均值。當 較大時漸近於,稱為關聯長度,的臨界行為是:
, ,或者,
而關聯函數本身的行為漸近於:
其中 是系統的空間維數。另外,序參量 隨壓力 的變化也有它的臨界行為,當時, 。一共有九個臨界指數。平均場理論給出的結果與實驗值存在微小差異,可見平均場理論還有不足之處。
卡達諾夫強調標度變換的重要性,他用標度變換,導出九個臨界指數間有七個相互滿足的關係式。所以,九個臨界指數中只有兩獨立指數,其他七個可由這些關係式導出。但為什麼可用標度變換的物理思想還沒有弄清。
1971年威耳孫認識到標度變換體現了重正化群的基本思想,它可不必通過複雜的配分函數解決統計物理中的相變,而是探索能使配分函數保持不變的變換性質,抓住相變的主要特徵。具體做法分兩個步驟:①由於T趨於T時,關聯長度ξ趨於無限大,元胞可用一定尺度的集團代替,集團中序參量平均值替代元胞的序參量。集團之間相互作用以有效作用代替。②進行標度變換使其與原來模型一致。這兩個步驟合起來用變換R表示。R一般是非線性變換。如此相繼進行R'=RR'變換。這些變換組稱為重正化群。最後在變換中的不動點同連續相變聯繫起來,給出臨界點相變的特徵。
從熱力學的觀點看,液氣共存對應於液相和氣相的化學勢相等,兩相的比容不等;關於相變的理論中,臨界現象是在連續相變點鄰近的現象(見相和相變、固體中的相變)。固體中有許多連續相變現象。連續相變往往是由於體系的對稱性改變,如位移型結構相變中是點陣的空間群改變;磁相變是晶體磁群改變;超導相變是規範對稱性改變(見超導微觀理論)。通常可以定義一個或幾個序參量來描述連續相變。它們在一個相(通常是對稱性高的相)為零,在另一個相(通常是對稱性低的相)不為零,而在相變點為零。相變時序參量連續變化。在氣-液臨界點的相變中,序參量可選為兩相的密度差或比容差;在鐵磁-順磁相變中可選固體的磁化強度,等等。藉助於重正化群理論,可以比較好地分析臨界現象,說明了空間維數與臨界指數的普適關係。從研究臨界現象發展起來的一系列新的概念與理論方法不僅對連續相變理論,而且對凝聚態物理與統計物理的許多分支,以及量子場論和粒子物理學都有深刻的影響。