流體力學
力學的分支
力學的一個分支,主要研究在各種力的作用下,流體本身的靜止狀態和運動狀態以及流體和固體界壁間有相對運動時的相互作用和流動規律。
流體力學是力學的一個分支,它主要研究流體本身的靜止狀態和運動狀態,以及流體和固體界壁間有相對運動時的相互作用和流動的規律。流體力學中研究得最多的流體是水和空氣。它的主要基礎是牛頓運動定律和質量守恆定律,常常還要用到熱力學知識,有時還用到宏觀電動力學的基本定律、本構方程和物理學、化學的基礎知識。 1738年伯努利出版他的專著時,首先採用了水動力學這個名詞並作為書名;1880年前後出現了空氣動力學這個名詞;1935年以後,人們概括了這兩方面的知識,建立了統一的體系,統稱為流體力學。除水和空氣以外,流體還指作為汽輪機工作介質的水蒸氣、潤滑油、地下石油、含泥沙的江水、血液、超高壓作用下的金屬和燃燒后產生成分複雜的氣體、高溫條件下的等離子體等等。發展簡史
流體力學(FluidMechanics)
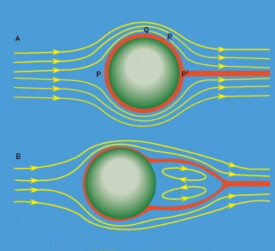
流體的流動曲線
流體力學中研究得最多的流體是水和空氣。它的主要基礎是牛頓運動定律和質量守恆定律,常常還要用到熱力學知識,有時還用到宏觀電動力學的基本定律、本構方程和物理學、化學的基礎知識。 1738年伯努利出版他的專著時,首先採用了水動力學這個名詞並作為書名;1880年前後出現了空氣動力學這個名詞;1935年以後,人們概括了這兩方面的知識,建立了統一的體系,統稱為流體力學。
應用領域
除水和空氣以外,流體還指作為汽輪機工作介質的水蒸氣、潤滑油、地下石油、含泥沙的江水、血液、超高壓作用下的金屬和燃燒后產生成分複雜的氣體、高溫條件下的等離子體等等。氣象、水利的研究,船舶、飛行器、葉輪機械和核電站的設計及其運行,可燃氣體或炸藥的爆炸,以及天體物理的若干問題等等,都廣泛地用到流體力學知識。許多現代科學技術所關心的問題既受流體力學的指導,同時也促進了它不斷地發展。1950年後,電子計算機的發展又給予流體力學以極大的推動。

流體力學
對流體力學學科的形成作出第一個貢獻的是古希臘的阿基米德,他建立了包括物理浮力定律和浮體穩定性在內的液體平衡理論,奠定了流體靜力學的基礎。此後千餘年間,流體力學沒有重大發展。直到15世紀,義大利達·芬奇的著作才談到水波、管流、水力機械、鳥的飛翔原理等問題;17世紀,帕斯卡闡明了靜止流體中壓力的概念。但流體力學尤其是流體動力學作為一門嚴密的科學,卻是隨著經典力學建立了速度、加速度,力、流場等概念,以及質量、動量、能量三個守恆定律的奠定之後才逐步形成的。
17世紀,力學奠基人牛頓研究了在流體中運動的物體所受到的阻力,得到阻力與流體密度、物體迎流截面積以及運動速度的平方成正比的關係。他針對粘性流體運動時的內摩擦力也提出了牛頓粘性定律。但是,牛頓還沒有建立起流體動力學的理論基礎,他提出的許多力學模型和結論同實際情形還有較大的差別。之後,法國皮托發明了測量流速的皮託管;達朗貝爾對運河中船隻的阻力進行了許多實驗工作,證實了阻力同物體運動速度之間的平方關係;瑞士的歐拉採用了連續介質的概念,把靜力學中壓力的概念推廣到運動流體中,建立了歐拉方程,正確地用微分方程組描述了無粘流體的運動;伯努利從經典力學的能量守恆出發,研究供水管道中水的流動,精心地安排了實驗並加以分析,得到了流體定常運動下的流速、壓力、管道高程之間的關係——伯努利方程。
歐拉方程和伯努利方程的建立,是流體動力學作為一個分支學科建立的標誌,從此開始了用微分方程和實驗測量進行流體運動定量研究的階段。從18世紀起,位勢流理論有了很大進展,在水波、潮汐、渦旋運動、聲學等方面都闡明了很多規律。法國拉格朗日對於無旋運動,德國赫爾姆霍茲對於渦旋運動作了不少研究……。在上述的研究中,流體的粘性並不起重要作用,即所考慮的是無粘流體。這種理論當然闡明不了流體中粘性的效應。
19世紀,工程師們為了解決許多工程問題,尤其是要解決帶有粘性影響的問題。於是他們部分地運用流體力學,部分地採用歸納實驗結果的半經驗公式進行研究,這就形成了水力學,至今它仍與流體力學并行地發展。1822年,納維建立了粘性流體的基本運動方程;1845年,斯托克斯又以更合理的基礎導出了這個方程,並將其所涉及的宏觀力學基本概念論證得令人信服。這組方程就是沿用至今的納維-斯托克斯方程(簡稱N-S方程),它是流體動力學的理論基礎。上面說到的歐拉方程正是N-S方程在粘度為零時的特例。
普朗特學派從1904年到1921年逐步將N-S方程作了簡化,從推理、數學論證和實驗測量等各個角度,建立了邊界層理論,能實際計算簡單情形下,邊界層內流動狀態和流體同固體間的粘性力。同時普朗克又提出了許多新概念,並廣泛地應用到飛機和汽輪機的設計中去。這一理論既明確了理想流體的適用範圍,又能計算物體運動時遇到的摩擦阻力。使上述兩種情況得到了統一。
20世紀初,飛機的出現極大地促進了空氣動力學的發展。航空事業的發展,期望能夠揭示飛行器周圍的壓力分佈、飛行器的受力狀況和阻力等問題,這就促進了流體力學在實驗和理論分析方面的發展。20世紀初,以儒科夫斯基、恰普雷金、普朗克等為代表的科學家,開創了以無粘不可壓縮流體位勢流理論為基礎的機翼理論,闡明了機翼怎樣會受到舉力,從而空氣能把很重的飛機托上天空。機翼理論的正確性,使人們重新認識無粘流體的理論,肯定了它指導工程設計的重大意義。機翼理論和邊界層理論的建立和發展是流體力學的一次重大進展,它使無粘流體理論同粘性流體的邊界層理論很好地結合起來。隨著汽輪機的完善和飛機飛行速度提高到每秒50米以上,又迅速擴展了從19世紀就開始的,對空氣密度變化效應的實驗和理論研究,為高速飛行提供了理論指導。20世紀40年代以後,由於噴氣推進和火箭技術的應用,飛行器速度超過聲速,進而實現了航天飛行,使氣體高速流動的研究進展迅速,形成了氣體動力學、物理-化學流體動力學等分支學科。

流體力學
石油和天然氣的開採,地下水的開發利用,要求人們了解流體在多孔或縫隙介質中的運動,這是流體力學分支之一——滲流力學研究的主要對象。滲流力學還涉及土壤鹽鹼化的防治,化工中的濃縮、分離和多孔過濾,燃燒室的冷卻等技術問題。燃燒離不開氣體,這是有化學反應和熱能變化的流體力學問題,是物理-化學流體動力學的內容之一。爆炸是猛烈的瞬間能量變化和傳遞過程,涉及氣體動力學,從而形成了爆炸力學。沙漠遷移、河流泥沙運動、管道中煤粉輸送、化工中氣體催化劑的運動等,都涉及流體中帶有固體顆粒或液體中帶有氣泡等問題,這類問題是多相流體力學研究的範圍。
等離子體是自由電子、帶等量正電荷的離子以及中性粒子的集合體。等離子體在磁場作用下有特殊的運動規律。研究等離子體的運動規律的學科稱為等離子體動力學和電磁流體力學,它們在受控熱核反應、磁流體發電、宇宙氣體運動等方面有廣泛的應用。
風對建築物、橋樑、電纜等的作用使它們承受載荷和激發振動;廢氣和廢水的排放造成環境污染;河床沖刷遷移和海岸遭受侵蝕;研究這些流體本身的運動及其同人類、動植物間的相互作用的學科稱為環境流體力學 (其中包括環境空氣動力學、建築空氣動力學)。這是一門涉及經典流體力學、氣象學、海洋學和水力學、結構動力學等的新興邊緣學科。
生物流變學研究人體或其他動植物中有關的流體力學問題,例如血液在血管中的流動,心、肺、腎中的生理流體運動和植物中營養液的輸送。此外,還研究鳥類在空中的飛翔,動物在水中的遊動,等等。
因此,流體力學既包含自然科學的基礎理論,又涉及工程技術科學方面的應用。此外,如從流體作用力的角度,則可分為流體靜力學、流體運動學和流體動力學;從對不同“力學模型”的研究來分,則有理想流體動力學、粘性流體動力學、不可壓縮流體動力學、可壓縮流體動力學和非牛頓流體力學等。
納維-斯托克斯方程(Navier-Stokes equations),以克勞德-路易·納維(Claude-Louis Navier)和喬治·蓋伯利爾·斯托克斯命名,是一組描述像液體和空氣這樣的流體物質的方程。這些方程建立了流體的粒子動量的改變率(加速度)和作用在液體內部的壓力的變化和耗散粘滯力(類似於摩擦力)以及重力之間的關係。這些粘滯力產生於分子的相互作用,能告訴我們液體有多粘。這樣,納維-斯托克斯方程描述作用於液體任意給定區域的力的動態平衡。
他們是最有用的一組方程之一,因為它們描述了大量對學術和經濟有用的現象的物理過程。它們可以用於建模天氣,洋流,管道中的水流,星系中恆星的運動,翼型周圍的氣流。它們也可以用於飛行器和車輛的設計,血液循環的研究,電站的設計,污染效應的分析,等等。
納維-斯托克斯方程依賴微分方程來描述流體的運動。這些方程,和代數方程不同,不尋求建立所研究的變數(譬如速度和壓力)的關係,而是建立這些量的變化率或通量之間的關係。用數學術語來講,這些變化率對應於變數的導數。這樣,最簡單情況的0粘滯度的理想流體的納維-斯托克斯方程表明加速度(速度的導數,或者說變化率)是和內部壓力的導數成正比的。
這表示對於給定的物理問題的納維-斯托克斯方程的解必須用微積分的幫助才能取得。實用上,只有最簡單的情況才能用這種方法解答,而它們的確切答案是已知的。這些情況通常設計穩定態(流場不隨時間變化)的非湍流,其中流體的粘滯係數很大或者其速度很小(小的雷諾數)。
對於更複雜的情形,例如厄爾尼諾這樣的全球性氣象系統或機翼的升力,納維-斯托克斯方程的解必須藉助計算機。這本身是一個科學領域,稱為計算流體力學。
進行流體力學的研究可以分為現場觀測、實驗室模擬、理論分析、數值計算四個方面:現場觀測是對自然界固有的流動現象或已有工程的全尺寸流動現象,利用各種儀器進行系統觀測,從而總結出流體運動的規律,並藉以預測流動現象的演變。過去對天氣的觀測和預報,基本上就是這樣進行的。不過現場流動現象的發生往往不能控制,發生條件幾乎不可能完全重複出現,影響到對流動現象和規律的研究;現場觀測還要花費大量物力、財力和人力。因此,人們建立實驗室,使這些現象能在可以控制的條件下出現,以便於觀察和研究。同物理學、化學等學科一樣,流體力學離不開實驗,尤其是對新的流體運動現象的研究。實驗能顯示運動特點及其主要趨勢,有助於形成概念,檢驗理論的正確性。二百年來流體力學發展史中每一項重大進展都離不開實驗。
模型實驗在流體力學中佔有重要地位。這裡所說的模型是指根據理論指導,把研究對象的尺度改變(放大或縮小)以便能安排實驗。有些流動現象難於靠理論計算解決,有的則不可能做原型實驗(成本太高或規模太大)。這時,根據模型實驗所得的數據可以用像換算單位制那樣的簡單演演算法求出原型的數據。現場觀測常常是對已有事物、已有工程的觀測,而實驗室模擬卻可以對還沒有出現的事物、沒有發生的現象(如待設計的工程、機械等)進行觀察,使之得到改進。因此,實驗室模擬是研究流體力學的重要方法。
理論分析是根據流體運動的普遍規律如質量守恆、動量守恆、能量守恆等,利用數學分析的手段,研究流體的運動,解釋已知的現象,預測可能發生的結果。理論分析的步驟大致如下:首先是建立“力學模型”,即針對實際流體的力學問題,分析其中的各種矛盾並抓住主要方面,對問題進行簡化而建立反映問題本質的“力學模型”。流體力學中最常用的基本模型有:連續介質、牛頓流體、不可壓縮流體、理想流體、平面流動等。
其次是針對流體運動的特點,用數學語言將質量守恆、動量守恆、能量守恆等定律表達出來,從而得到連續性方程、動量方程和能量方程。此外,還要加上某些聯繫流動參量的關係式(例如狀態方程),或者其他方程。這些方程合在一起稱為流體力學基本方程組。求出方程組的解后,結合具體流動,解釋這些解的物理含義和流動機理。通常還要將這些理論結果同實驗結果進行比較,以確定所得解的準確程度和力學模型的適用範圍。
從基本概念到基本方程的一系列定量研究,都涉及到很深的數學問題,所以流體力學的發展是以數學的發展為前提。反過來,那些經過了實驗和工程實踐考驗過的流體力學理論,又檢驗和豐富了數學理論,它所提出的一些未解決的難題,也是進行數學研究、發展數學理論的好課題。按數學發展的水平看,有不少題目將是在今後幾十年以內難於從純數學角度完善解決的。在流體力學理論中,用簡化流體物理性質的方法建立特定的流體的理論模型,用減少自變數和減少未知函數等方法來簡化數學問題,在一定的範圍是成功的,並解決了許多實際問題。對於一個特定領域,考慮具體的物理性質和運動的具體環境后,抓住主要因素忽略次要因素進行抽象化也同時是簡化,建立特定的力學理論模型,便可以克服數學上的困難,進一步深入地研究流體的平衡和運動性質。
20世紀50年代開始,在設計攜帶人造衛星上天的火箭發動機時,配合實驗所做的理論研究,正是依靠一維定常流的引入和簡化,才能及時得到指導設計的流體力學結論。此外,流體力學中還經常用各種小擾動的簡化,使微分方程和邊界條件從非線性的變成線性的。聲學是流體力學中採用小擾動方法而取得重大成就的最早學科。聲學中的所謂小擾動,就是指聲音在流體中傳播時,流體的狀態(壓力、密度、流體質點速度)同聲音未傳到時的差別很小。線性化水波理論、薄機翼理論等雖然由於簡化而有些粗略,但都是比較好地採用了小擾動方法的例子。每種合理的簡化都有其力學成果,但也總有其局限性。例如,忽略了密度的變化就不能討論聲音的傳播;忽略了粘性就不能討論與它有關的阻力和某些其他效應。掌握合理的簡化方法,正確解釋簡化后得出的規律或結論,全面並充分認識簡化模型的適用範圍,正確估計它帶來的同實際的偏離,正是流體力學理論工作和實驗工作的精華。
流體力學的基本方程組非常複雜,在考慮粘性作用時更是如此,如果不靠計算機,就只能對比較簡單的情形或簡化后的歐拉方程或N-S方程進行計算。20世紀30~40年代,對於複雜而又特別重要的流體力學問題,曾組織過人力用幾個月甚至幾年的時間做數值計算,比如圓錐做超聲速飛行時周圍的無粘流場就從1943年一直算到1947年。
1、船舶與海洋結構物流體性能:高等流體力學,船舶與海洋結構物水動力學,船舶與海洋結構物載荷與動力響應,船舶與海洋結構物運動與控制等。 2、計算流體力學及應用:高等流體力學,粘性流體力學,計算流體力學,流體力學中的數值計算方法,包括網格生成技術、湍流模型、運動邊界追蹤技術,仿生推進技術等。 3、流體與固體的耦合力學分析 高等流體力學,結構力學,船舶與海洋結構物水動力學,水彈性力學,船舶與海洋結構物載荷與動力響應,海洋結構物與波浪的相互作用等。
流體力學有一些基本假設,基本假設以方程的形式表示。例如,在三維的不可壓縮流體中,質量守恆的假設的方程如下:在任意封閉曲面(例如球體)中,由曲面進入封閉曲面內的質量速率,需和由曲面離開封閉曲面內的質量速率相等。(換句話說,曲面內的質量為定值,曲面外的質量也是定值)以上方程可以用曲面上的積分式表示。
流體力學假設所有流體滿足以下的假設:
·質量守恆
·動量守恆
·連續體假設
在流體力學中常會假設流體是不可壓縮流體,也就是流體的密度為一定值。液體可以算是不可壓縮流體,氣體則不是。有時也會假設流體的黏度為零,此時流體即為非粘性流體。氣體常常可視為非粘性流體。若流體黏度不為零,而且流體被容器包圍(如管子),則在邊界處流體的速度為零。
從阿基米德到現在的二千多年,特別是從20世紀以來,流體力學已發展成為基礎科學體系的一部分,同時又在工業、農業、交通運輸、天文學、地學、生物學、醫學等方面得到廣泛應用。
今後,人們一方面將根據工程技術方面的需要進行流體力學應用性的研究,另一方面將更深入地開展基礎研究以探求流體的複雜流動規律和機理。后一方面主要包括:通過湍流的理論和實驗研究,了解其結構並建立計算模式;多相流動;流體和結構物的相互作用;邊界層流動和分離;生物地學和環境流體流動等問題;有關各種實驗設備和儀器等。