雲理論

李德毅老師開創的"雲"理論，是對傳統的隸屬函數概念的揚棄。自然界中大量模糊概念可以用正態雲來刻劃的事實，導致了對正態雲外部特徵以及內部機理的深入研究。模糊概念可表述為一個邊界具有不同彈性的，收斂於正態分佈函數的"雲"。實質上，雲是用語言值表示的某個定性概念與其定量表示之間的不確定性轉換模型，雲的數字特徵可用期望值Ex、熵En、超熵He三個數值來表徵，它把模糊性和隨機性完全集成到一起，構成定性和定量相互間的映射，為定性與定量相結合的信息處理提供了有力手段。所以它成為令人矚目的處理模糊信息的有效工具。

雲是用語言值表示的某個定性概念與其定量表示之間的不確定轉換模型，它主要反映宇宙中事物或人類知識中概念的兩種不確定性：模糊性(邊界的亦此亦彼性)和隨機性(發生的概率)，用雲模型把模糊性和隨機性完全集成在一起，研究自然語言中的最基本的語言值(又稱語言原子)所蘊含的不確定性的普遍規律，使得有可能從語言值表達的定性的信息中獲得定量數據的範圍和分佈規律，也有可能從精確數值有效轉換為恰當的定性語言值。

設X是一個精確數值量的集合X={x},稱為論域，關於論域X上對應的定性概念，是指對於任意數值量，都存在一個有穩定傾向的隨機數，叫作x對的隸屬度，隸屬度在論域上的分佈稱為隸屬雲，簡稱為雲，它由許許多多雲滴組成，某一個雲滴也許無足輕重，但云的整體形狀反映了定性概念的重要特性。因為這種分佈很類似天空中的雲彩，遠看有明確的形狀，近看沒有確定的邊界，所以借用雲來比喻定性和定量之間的不確定性映射。

不確定性的概念的整體特性可以用雲的數字特徵來反映，這是定性概念的整體定量特性，對於理解定性概念的內涵和外延有著重要的意義。

①雲的期望 Ex(Expected value)，雲滴在論域空間的分佈期望，就是最能代表定性概念的點，也是這個概念量化的最典型樣本。

②熵 En(Entropy)，定性概念的不確定性度量，由概念的隨機性和模糊性共同決定。一方面 En是定性概念隨機性的度量，反映了能夠代表這個定性概念的雲滴的離散程度；另一方面又是定性概念亦此亦彼性的度量，反映了論域空間中可被概念接受的雲滴的取值範圍。

③超熵 He(Hyper entropy)，超熵是熵的不確定性的度量，即是熵的熵，由熵的隨機性和模糊性共同決定。

雲模型是雲的具體實現方法，也是基於雲的運算、推理和控制等的基礎，由定性概念到定量表示的過程，也就是有雲的數字特徵產生雲滴的具體實現，稱為正向雲發生器；由定量表示到定性概念的過程，也就是由雲滴得到雲的數字特徵的具體實現，稱為逆向雲發生器。

由於在概率論與隨機過程的理論研究和實際應用中，正態分佈起著特別重要的作用，在各種概率分佈中居於首要的地位，其概率分佈的形式廣泛存在於自然現象、社會現象、科學技術以及生產活動中，，在實際中遇到的許多隨機現象都服從或近似服從正態分佈。而且，中心極限定理也在理論上闡述了產生正態分佈的條件，體現了其的廣泛性和普適性。

另外，在模糊集理論中，隸屬函數是模糊理論的基石，但自然和社會科學中的大量模糊概念的隸屬函數，並沒有嚴格的確定方法，在通常的經驗下最為常見的隸屬函數是鐘形隸屬函數，這與正態分佈的分佈函數的一致的。

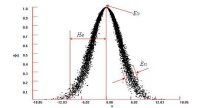
以一般來講，以正態雲模型作為代表，是具有普遍性的。而且從介紹簡單起見，我們介紹一維正態雲模型，如圖所示。此圖由數字特徵(0, 3, 0.3)，以及10000個雲滴生成。

雲發生器是從定性概念到定量表示的過程，也就是有雲的數字特徵產生雲滴的具體實現。下面具體說明正向及逆向正態雲發生器以及 X雲發生器和 Y雲發生器。

當概念對應的數域為一維時，正態雲發生器的演演算法如下：

（ Ex， En， He）→ Drop ( x, y)

X雲發生器和 Y雲發生器就是指在已知雲的三個數字特徵( Ex, En, He)的前提下，還已知特定的 x=x0或者 y=y0條件，所以也叫 X條件雲發生器和 Y條件雲發生器，由於 y=y0表示已知的是特定的隸屬度， Y條件雲發生器也叫做隸屬度條件雲發生器， X條件雲發生器和 Y條件雲發生器是基於雲模型的不確定性推理的基礎，比如將 X條件雲與 Y條件雲相連接就構成了一個單條件規則發生器。

所謂逆向雲發生器是指從定量表示到定性概念的過程，也就是由雲滴得到雲的數字特徵的具體實現，如下所示：

( x1, y1)，( x2, y2)，( x3, y3)…… →（ Ex， En， He）

按雲的產生機理和計算方向有以下分類：

雲的應用範圍很廣，目前雲模型被成功地用於人工智慧、跳頻雲發生器、C3I系統的效能評估中。