約翰·伯努利

約翰·伯努利（Johann Bernoulli,1667.8.6-1748.1.1）是老尼古拉·伯努利（Nikolaus Bernoulli，1623—1708）的第三個兒子，雅格布·伯努利(Jakob Bernoulli）的弟弟．幼年時他父親像要求雅格布一樣，試圖要他去學經商，他認為自己不適宜從事商業，拒絕了父親的勸告．1683年進入巴塞爾大學學習，1685年通過邏輯論文答辯，獲得藝術碩士學位．接著他攻讀醫學，1690年獲醫學碩士學位，1694年又獲博士學位．

約翰在巴塞爾大學學習期間，懷著對數學的熱情，跟其哥哥雅格布秘密學習數學，並開始研究數學．兩人都對無窮小數學產生了濃厚的興趣，他們首先熟悉了G．W．萊布尼茲（Leibniz）的不易理解的關於微積分的簡略論述．正是在萊布尼茲的思想影響和激勵下，約翰走上了研究和發展微積分的道路．

1691年6月，約翰在《教師學報》（Acta eruditorum）上發表論文，解決了雅格布提出的關於懸鏈線的問題．這篇論文的發表，使他加入了C．惠更斯（Huygens）、萊布尼茲和I．牛頓(Newton）等數學家的行列．

1691年秋天，約翰到達巴黎．在巴黎期間他會見了G．F．A．de洛比達（L’Hospital），並於1691—1692年間為其講授微積分．二人成為親密的朋友，建立了長達數十年之久的通信聯繫．洛比達以後成為法蘭西最有才能的數學家之一．

1691—1692年間，約翰寫了世界上第一本關於微積分的教科書，積分學部分於1742年出版，微分學部分直到1924年才出版．

1693年約翰開始與萊布尼茲建立了通信聯繫，信中就一些數學問題交換意見．約翰是萊布尼茲的忠實擁護者，以至被捲入了萊布尼茲與牛頓關於微積分優先權的爭論，他極力為萊布尼茲辯護，並猛烈地批評甚至嘲笑英國人．法國巴黎科學院院士P．瓦里尼翁（Varignon）也是約翰的密友，二人之間也進行了通信聯繫．

1695年，約翰獲得荷蘭格羅寧根大學數學教授的職務．他接受職務后，工作特別努力，一面認真教學，一面在微積分方面做出了許多新的貢獻．1705年，約翰的哥哥雅格布去世，他去巴塞爾大學繼任數學教授的職務，致力於數學教學，直到1748年去世．

由於約翰長期的教學活動和他對數學的貢獻，受到當時科學界的高度評價．1699年被選為巴黎科學院的國外院士；1701年被接受為柏林科學協會（即後來的柏林科學院）的會員；1712年被選為英國皇家學會的會員；1724年被選為義大利波倫亞科學院的國外院士；1725年被選為彼得堡科學院的國外院士．他還在巴塞爾擔任名譽官職，是地方教育委員會的成員，成為當時巴塞爾的知名人物．

約翰由於在力學、天體力學、流體力學方面的研究成果，曾分別於1724年、1730年和1735年三次獲得巴黎科學院的獎賞．特別是1735年與他的兒子丹尼爾·伯努利(Daniel Bernoulli）共同完成的關於行星軌道理論的獲獎文章，受到人們的高度重視．

約翰生活在17世紀下半葉到18世紀上半葉．這一時期數學上最突出的成就就是微積分的發明與發展．由微積分的創立，又產生了數學的一些重要分支，如微分方程、無窮級數、微分幾何、變分法等．18世紀數學家的主要任務是致力於這些學科分支的發展，而要完成這些任務，首先必須發展、完善微積分本身．約翰就是一個對微積分和與其相關的許多數學分支都做過重要貢獻的人，是18世紀分析學的重要奠基者之一．

約翰首先使用“變數”這個詞，並且使函數概念公式化．1698年他從解析的角度提出了函數的概念：“由變數x和常數所構成的式子叫做x的函數”，記作X或ξ，1718年他又改用φx表示x的函數．記號f(x）是歐拉於1734年才引進的．約翰對一些具體函數進行過研究，除一般的代數函數外，他還引入了超越函數，即三角函數、對數函數、指數函數、變數的無理數次冪函數及某些用積分表達的函數．指出對數函數是指數函數的反函數．

約翰對微積分的貢獻主要是對積分法的發展．他曾採用變數替換來求某些函數的積分，在1699年的《教師學報》上給出了用變數替換計算積分

的方法，作變換，就可以把積分化為形式的積分。但約翰在1702年注意到

從而立即可以把積分求出。這種方法就是把一個分式分解為部分分式的方法。把有理函數化為部分分式積分的方法是約翰的重大貢獻。設p(x)和q(x)都是x的多項式，若p(x)的次數高於q(x)的次數，首先作除法將化為一個多項式與一個真分式之和的形式，多項式部分積分是容易的。對於的積分，約翰有一個重要發現，首次提出了部分分式的積分方法，即

這裡a,b,c以及f,q,h等均為常數。於是

這就完成了這個積分。依據這種分析，約翰在1702年的《教師學報》上就斷言，任何有理函數的積分，無需包含三角函數與對數函數以外的任何其他超越函數，因為有理數的分母是x的一個n次多項式。在約翰給萊布尼茲的信中，就曾用部分分式法來求積分

但是，由於的一次因子可能是複數，這就導致了約翰、萊布尼茲及歐拉之間關於複數的對數和負數的對數的爭論，這種爭論推動了複變函數的發展和歐拉公式的建立。即

約翰還提出了現在微積分中的一個著名定理——洛比達定理（或法則），它是用導數求一個分式當分子和分母都趨於零（或無窮大）時的極限的．這個定理是由他的學生洛比達在1696年編寫的一本非常有影響的微積分教材《無窮小分析》（Analyse des infiniment petits）中引入的，后稱為洛比達法則．這個法則實際上是1694年約翰給洛比達的信中告訴洛比達的．

1742年約翰出版了他的著作《積分學教程》（Lections mathematies de method integralium），在這本書中約翰彙集了他在微積分方面的研究成果，他不僅給出了各種不同的積分方法的例子，還給出了曲面的求積，曲線的求長和不同類型的微分方程的解法，使微積分更加系統化．這部著作成為微積分學發展中的一本重要著作，在當時對於推動微積分的發展和普及微積分的知識都起了積極的作用．

微積分的迅速發展和應用，必然導致了微分方程這門新學科的誕生．其實微分方程的發展是與微積分的發展交織在一起的．約翰在這方面也是一位開拓者．

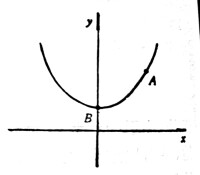
1691年6月約翰在《教師學報》上發表文章，解決了他哥哥雅格布提出的“懸鏈線”問題，即“一根柔軟而不能伸長的繩子自由懸掛於兩固定點，求這繩所形成的曲線”．約翰設法列出了該問題的微分方程

其中s是由B點到任一點A之間的弧長，而a是A點處繩的張力在水平方向的分量與單位繩長重力的比值．通過解此方程就得到懸鏈線的方程。這是雙曲餘弦函數。約翰對解決懸鏈線問題大為得意。在此基礎上，約翰與雅格布還在1691—1692年間解決了懸掛著的變密度非彈性軟繩、等厚度的彈性繩、以及在每一點上的作用力都指向一個固定中心的細繩所形成的形狀的問題。

約翰和萊布尼茲在1694年引進了找等交曲線族的問題，即找一曲線或曲線族，使得與已知曲線族相交成給定的角．約翰稱等交曲線為軌線．他將這個問題作為向雅格布的一個挑戰．雅格布只解決了一些特殊的實例，約翰導出了一特殊曲線族的正交軌線的微分方程，並在1698年找到了它的解．這個問題後來由萊布尼茲與雅格布的學生J．赫曼（Jacob Hermann）得到較完美的解決．

在求解1695年雅格布給出的“伯努利方程”

時，萊布尼茲採用變數替換法，使方程化為線性方程。而約翰提出了另一種解法，他設想把函數y分解為兩個關於x的函數M(x)與N(x)的乘積，即y=M(x)N(x),於是方程化為

函數M(x),N(x)帶有很大的任意性，令

即取，則方程又化為

這個方程容易求出它的解N(x)，於是就得到了伯努利方程的解y=M(x)N(x)。約翰這種解方程的思想，在求解二階偏微分方程時，得到了應用。

1727年，約翰在一篇論文中研究了弦振動問題，考慮一根無重量的彈性弦，在弦上等間隔地放置著n個等質量的質點，當放置6個質點時，他得到弦的簡諧振動方程。他用分析的方法解出了此方程，從而證明了在任何時刻弦的形狀必定是正弦曲線．這一事實也出現在約翰給他的兒子丹尼爾的信中．約翰後來還解決了一個拋射體在阻力正比於速度的任何次冪的介質中運動的問題，得到它的微分方程為

變分法的產生和發展，最初來自三大問題：最速降線問題，等周問題和測地線問題．約翰在這些問題的研究中都做出了貢獻．

約翰在1696年6月號的《教師學報》上提出了一個作為向雅格布和歐洲數學家挑戰的題目：設不在同一鉛直線上的兩點A與B，使一質點只在重力的影響下從A點滑向B點，求所需時間最短的途徑（摩擦和空氣阻力不計）．這就是最速降線問題．對這個問題，牛頓、萊布尼茲、洛比達、雅格布·伯努利和約翰·伯努利都得到了正確的解答．最速降線是一條聯結A，B兩點的上凹的旋輪線（又稱圓滾線或擺線）．他們的答案相同，而解法各異．除雅格布的解法外，其他人的解法都發表在1697年5月號的《教師學報》上．後來歐拉和J．L．拉格朗日（Lagrange）給出了這類問題的一般解法．在這個問題的解決過程中，顯示了約翰的才能，他是通過機靈的直覺解決這個問題的．他將這一機械問題，通過已有的費馬最小時間原理的分析轉化為光學問題，從光的折射定律推出了旋輪線的微分方程．雅格布從另一個角度給出了一個較麻煩但更一般的解法．伯努利兄弟對旋輪線是最速降線問題的解感到驚奇和振奮，約翰說：“我們之所以欽佩惠更斯，是因為他首先發現了在一個旋輪線上的大量質點下落，它們總是同時到達，與質點的起始位置無關緊要．然後，當你聽到我肯定說旋輪線就是惠更斯的等時曲線的時候，可能驚訝得簡直發獃．等時曲線是最速降線我們看得很清楚．”

在1697年5月號的《教師學報》上，雅格布·伯努利提出了一個含幾種情形的相當複雜的等周問題（即在給定周長的所有封閉曲線中求一條曲線，使得它所圍的面積最大），作為向約翰的挑戰．約翰開始過低地估計了這個問題的複雜性，沒有弄清這個變數問題的特性，所以在1697年和1701年兩次給出的解答都沒有得到成功，這受到了雅格布無情的批評．1700年5月雅格布在《教師學報》上發表了關於等周問題的解，指出這條曲線是一個圓．1718年，約翰繼續研究了等周問題，他沿著雅格布的思路，改進了雅格布的解法，在《科學院論文集》（Memoires de l’Académie dessciences）中約翰的論文給出了一個精確的、形式上漂亮的等周問題的解法．這篇論文包含了關於變分法的現代方法的核心，提出了變分法的一些概念，奠定了變分法的基礎．

約翰與他的哥哥雅格布還對測地線問題進行了研究．測地線是指曲面上兩點間長度最短的路徑．1697年，約翰在《博學雜誌》（Journal des scavans）中，提出了在凸曲面上求兩點間的最短弧問題，1698年8月26日，他還寫信給萊布尼茲，談到他覺察到的測地線的特有的性質．1698年，雅格布解決了錐面和旋轉面上的測地線問題，1728年約翰又用雅格布的方法取得了一些進展，並且求得了另外幾類曲面的測地線．由於在最速降線問題、等周問題及測地線問題的研究中約翰的出色工作，使之成為變分法的先驅者之一．

此外，約翰在數學的其他領域，如解析幾何等學科中，也做過一些有益的工作．1715年約翰在給萊布尼茲的信中引進了現在通用的用三個坐標平面建立空間坐標系的方法，提出了用三個坐標變數的方程表示曲面的方法。

約翰不僅在純數學方面做了大量的工作，而且他在把微積分應用到物理學特別是力學和天體力學方面所作的著述，也有很高的價值。

約翰對一些力學上的概念作出了準確的解釋．1714年，他發表了《軍艦操作技術原理》（Theorie de la manoeuvre des vaisse-aux），在這本書中，他澄清了笛卡兒理論中關於力與“能量”（當時稱為vis viva）的混亂．1715年，他又提出了所謂虛擬（virtual）速度原理。

1727年，他發表了論文“論運動的交換規律”（Discourssur leslois de la communication du mouvement），在這篇論文中，討論了行星的橢圓軌道和行星軌道的傾斜度．但是在引力理論方面，由於他的偏見，不支持牛頓的理論，而且為笛卡兒的旋渦理論辯護，推遲了牛頓力學在歐洲大陸的傳播。

在實驗物理方面，他研究了光學現象，提出了焦散面理論．在1692年的《教師學報》中，他得到了某些焦散面方程，例如當一束平行光線投射到球面鏡上時，從球面上反射出來的光線的焦散面方程．他還把最速降線問題的研究擴展到了可以確定光線在各種不同密度的介質中所通過的路徑．他還研究了弦振動問題及水力學等問題，提出過二階甚至三階的方程。

約翰·伯努利是17—18世紀在歐洲有影響的數學家．約翰在他的科學生涯中，採用通信等方式與其他科學家建立了廣泛的聯繫，交流學術成果，討論和辯論一些問題，這是他學術活動的一大特點．他與110位學者有通信聯繫，進行學術討論的信件大約有2500封，這大大促進了學術的發展．約翰一生另一特點是致力於教學和培養人才的工作，他培養出一批出色的數學家，其中包括18世紀數學界中心人物歐拉，這不能不說是約翰·伯努利的功績之一。

代數學與統計學

伯努力在代數學和統計學也有充分的研究。在代數學，他研究自己的伯努利不等式，這個不等式為許多解方程的題給了一個捷徑。在統計學裡面，他還發現了三大大數定律之一中的伯努利大數定律，為概率學做出了巨大貢獻。