ARC

正弦函數和它的反函數：f(x)=sinx->f(x)=arcsinx

餘弦函數和它的反函數：f(x)=cosx->f(x)=arccosx

正切函數和它的反函數：f(x)=tanx->f(x)=arctanx

餘切函數和它的反函數：f(x)=cotx->f(x)=arccotx

數學里arc是反三角函數的符號，適用於表達不特殊的角的大小，我們知道特殊角如30°的tan值，sin值和cos值都是一個特殊的數，但是在解決一些題的時候會出現某一個角的三角函數值不特殊，我們又沒有反三角函數表，所以不清楚這個角的大小，arc的作用就是表示這種不特殊的角，其中涉及增減性的問題。

反三角函數是一種基本初等函數。它並不能狹義的理解為三角函數的反函數，是個多值函數。它是反正弦arcsin x，反餘弦arccos x，反正切arctan x，反餘切arccot x這些函數的統稱，各自表示其正弦、餘弦、正切、餘切為x的角。

三角函數的反函數不是單值函數，因為它並不滿足一個自變數對應一個函數值的要求，其圖像與其原函數關於函數y=x對稱。歐拉提出反三角函數的概念，並且首先使用了“arc+函數名”的形式表示反三角函數，而不是。

為限制反三角函數為單值函數，將反正弦函數的值y限在-π/2≤y≤π/2，將y作為反正弦函數的主值，記為y=arcsin x；相應地，反餘弦函數y=arccos x的主值限在0≤y≤π；反正切函數y=arctan x的主值限在-π/2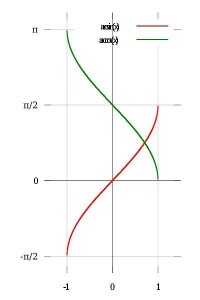

反正弦函數

y=sin x在[-π/2，π/2]上的反函數，叫做反正弦函數。記作arcsinx，表示一個正弦值為x的角，該角的範圍在[-π/2，π/2]區間內。定義域[-1，1] ，值域[-π/2，π/2]。

反餘弦函數

y=cos x在[0，π]上的反函數，叫做反餘弦函數。記作arccosx，表示一個餘弦值為x的角，該角的範圍在[0，π]區間內。定義域[-1，1] ，值域[0，π]。

反正切函數

y=tan x在(-π/2，π/2）上的反函數，叫做反正切函數。記作arctanx，表示一個正切值為x的角，該角的範圍在（-π/2，π/2）區間內。定義域R，值域（-π/2，π/2）。

反餘切函數

y=cot x在（0，π）上的反函數，叫做反餘切函數。記作arccotx，表示一個餘切值為x的角，該角的範圍在（0，π）區間內。定義域R，值域（0，π）。

綠的為y=arccot(x) 紅的為y=arctan(x)

反正割函數

y=sec x在[0,π/2)U(π/2,π]上的反函數，叫做反正割函數。記作arcsecx，表示一個正割值為x的角，該角的範圍在[0,π/2)U(π/2,π]區間內。定義域（-∞,-1]U[1,+∞),值域[0,π/2)U(π/2,π]。

反餘割函數

y=csc x在[-π/2,0)U(0,π/2]上的反函數，叫做反餘割函數。記作arccscx，表示一個餘割值為x的角，該角的範圍在[-π/2,0)U(0,π/2]區間內。定義域（-∞,-1]U[1,+∞),值域[-π/2,0)U(0,π/2]。