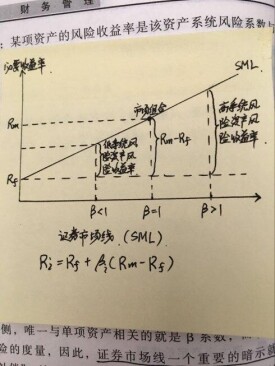
證券市場線
資本資產定價模型的圖示形式
資本資產定價模型(CAPM)的圖示形式稱為證券市場線(SML)。它主要用來說明投資組合報酬率與系統風險程度β係數之間的關係,以及市場上所有風險性資產的均衡期望收益率與風險之間的關係。
證券市場線方程對任意證券或組合的期望收益率和風險之間的關係提供十分完整的闡述,其方程為E(rP)=rF+[E(rM)-rF]βP。任意證券或組合的期望收益率由兩部分構成:一部分是無風險利率rF,它是由時間創造的,是對放棄即期消費的補償;另一部分[E(rM)-rF]βp是對承擔風險的補償,稱為“風險溢價”,它與承擔的系統風險β係數的大小成正比。 [E(rM)-rF]其中的代表了對單位風險的補償,通常稱之為風險的價格。
證券市場線是以Ep為縱坐標、βp為橫坐標的坐標系中的一條直線,它的方程是:Ri=Rf+βi(Rm-Rf)。其中:R和β分別表示證券或證券組合的必要報酬率和β係數,證券市場線表明證券或組合的要求的收益與由β係數測定的風險之間存在線性關係。
1.β係數的意義
證券市場線描述的則是市場均衡條件下單項資產或資產組合(不論它是否已經有效分散風險)的期望收益與風險之間的關係。測度風險工具是單項資產或資產組合對於整個市場組合方差的貢獻程度,即β係數。它告訴我們相對於市場組合而言特定資產的系統風險是多少。
舉例:普通股成本,資本資產定價模型中的貝塔值的估計
貝塔值是企業的權益收益率與股票市場收益率的協方差:
β=cov(Ri,Rm)/б^2
б^2是市場指數的方差。
2.β係數的確定
在確定計算貝塔值時,必須做出兩項選擇
(1)選擇有關預測期間的長度【5年或更長】。
公司風險特徵無重大變化時,可以採用5年或更長的預測長度;如果公司風險特徵發生重大變化,應當使用變化后的年份作為預測期長度。
(2)選擇收益計量的時間間隔。
使用每周或每月的收益率被廣泛採用。
(3)財務估價使用的現金流量數據是面向未來的,而計算權益成本使用的β值卻是歷史的,時間基礎不一致的問題
證券市場線方程對任意證券或組合的期望收益率和風險之間的關係提供了十分完整的闡述。任意證券或組合的期望收益率由兩部分構成:一部分是無風險利率,它是由時間創造的,是對放棄即期消費的補償;另一部分則是對承擔風險的補償,通常稱為“風險溢價”。它與承擔的風險的大小成正比。其中的代表了對單位風險的補償,通常稱之為風險的價格。
1、“證券市場線”的橫軸是“貝塔係數(只包括系統風險)”;“資本市場線”的橫軸是“標準差(既包括系統風險又包括非系統風險)”。
2、資本市場線是由風險資產和無風險資產構成的投資組合的有效邊界。僅適用於有效組合。測度風險的工具是整個資產組合的標準差。
證券市場線描述的是市場均衡條件下單項資產或資產組合(無論是否已經有效地分散風險)的期望收益與風險之間的關係。適用於單項資產或資產組合(無論是否有效分散風險)。測度風險的工具是單項資產或資產組合的β係數。
3、“證券市場線”揭示的是“證券的本身的風險和報酬”之間的對應關係;“資本市場線”揭示的是“持有不同比例的無風險資產和市場組合情況下”風險和報酬的權衡關係。
5、證券市場線表示的是“要求收益率”,即投資“前”要求得到的最低收益率;而資本市場線表示的是“期望報酬率”,即投資“后”期望獲得的報酬率。
6、證券市場線的作用在於根據“必要報酬率”,利用股票估價模型,計算股票的內在價值;資本市場線的作用在於確定投資組合的比例;
7、資本市場線和證券市場線的斜率都表示風險價格,但含義不同,前者表示整體風險的風險價格,後者表示系統風險的風險價格。計算公式也不同:
資本市場線斜率=(風險組合的期望報酬率-無風險報酬率)/風險組合的標準差
證券市場線斜率=市場組合要求的收益率-無風險收益率,即Rm-Rf,也稱風險溢價。