橢球面大地測量學

橢球面大地測量學研究的主要問題是：橢球面上大地線和法截線的性質；橢球面三角形的解算；大地測量主題的解算；橢球面投影到平面上的問題，以便將大地坐標換算為平面坐標；一橢球面同另一橢球面的關係，以實現不同大地坐標系的換算。

橢球面上點的表示和點間的聯繫：參考橢球面上一點G的坐標用大地經度L和大地緯度B表示（圖1[地球橢球的幾何元素]）。

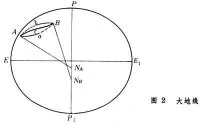
大地經度L為 G點的子午面PGP′同起始子午面PEP′間的交角，從起始子午面分別向東和向西量度，各由0°～180°；向東為東經，向西為西經。大地緯度B為橢球面上G點的法線GN與赤道面 EQE′的交角，從赤道面分別向北極P和南極 P′量度，各由0°～90°；向北為北緯，向南為南緯。橢球面上兩點間用大地線連接。大地線是橢球面上兩點間距離最短的曲線（圖2[大地線]）。

設AB為橢球面上的兩點，PP′為橢球的短軸，A和B點的法線分別為AN和BN;由A點法線與B點構成的法面ABN一般不同由B點法線與A構成的法面BANB重合，它們同橢球面的截曲線分別是AB和AbB，稱為相對法截線。為了消除橢球面上兩點間連線的這種非惟一性，大地測量中規定用橢球面上A、B兩點間的大地線 AcB（通常位於兩條相對法截線之間）為地面上相應兩點的投影線。橢球面上的一切計算公式都是依據大地線推導的。例如，利用大地線的特性及其與法截線的關係，可以推出法截線化為大地線方向的改正公式，照準點高出橢球面所引起的方向改正公式，以及地面上測量的距離歸算至橢球面上的改正公式。

大地測量主題解算

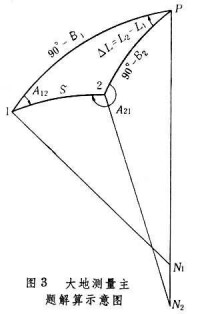
一般把在橢球面上解算點的大地坐標和點間的邊長、方位角這一類大地測量學的基本問題稱為大地測量主題解算（圖3[ 大地測量主題解算示意圖]）。

已知點1的大地經度L、大地緯度B1,以及點1至點2的大地線長度S和大地線方位角A，計算點 2和大地經度L、大地緯度B和點2至點1的大地線方位角 A，稱為大地測量主題正算問題。已知點1和點2的大地經度L和L，以及大地緯度B和B，計算兩點間的大地線長度S及其兩端的大地線方位角A和A,稱為大地測量主題反算問題。大地測量主題的解算，實質上就是解算圖3[ 大地測量主題解算示意圖]

所示的橢球面極三角形。由於橢球面三角形不如球面三角形那樣簡單，解算比較複雜，通常應用級數展開公式，並根據所需要的精度來決定級數的項數。解算的複雜性導致多種多樣的解算方法，歸納起來有3種類型：

第一類是以勒讓德級數為基礎，將兩點的經度差△L、緯度差△B和方位角差△A展開為大地線長度S的冪級數，其中各係數含有B、△L和A對S的各階導數，它們都需要利用大地線的微分關係式來求定。

第二類是利用一個輔助面作為解算的過渡面，例如經典的貝塞爾方法，就是採用一個球面作為輔助面，先確定橢球面上各元素同輔助球面上各元素之間的相應關係，再將橢球面上的已知元素換算到輔助球面上，在輔助球面上求解大地測量主題。最後，將輔助球面上解算的結果再換算至橢球面上。

第三類是利用大地線的基本微分方程，採取數值積分的方法，直接解算大地測量主題。這類解法的公式簡單，但用於中、長距離時的重複計算較大。

在大地控制網的洲際聯測中，在無線電導航以及洲際導彈發射技術中，中距離（1000公里以下）和長距離（1000公里以上）的大地測量主題解算有著重要作用。

大地坐標系的換算

大地坐標系是由所採用的橢球參數（長半軸和扁率）以及橢球在地球體內的定位確定的。如果採用了新的橢球，即改變了橢球參數；或者改變了橢球的定位，即改變了大地原點的起算數據；大地坐標系都將發生變化。大地坐標系有了變化，就要重新計算大地控制網中各點的大地坐標。如果根據新的起算數據和新的橢球參數，重新解算大地測量主題，計算工作量將非常繁重。實際上，橢球參數改變或定位改變所引起的大地坐標系各參數的變化都是很小的。因此，可以利用數學關係建立一種公式，在坐標變換時用以直接計算大地控制網中每一點大地坐標變化和每一邊方位角變化的改正數。這種公式稱為大地線微分公式。由於參考橢球重新定位（橢球參數不變）所引起的大地坐標和方位角改正數公式，稱為第一類微分公式。由於橢球參數的微小變化所引起的大地坐標和方位角改正數公式，稱為第二類微分公式。

兩個大地坐標系之間的關係，可用空間直角坐標系的形式來表達，即把大地點在空間直角坐標系中的坐標變化，用以兩個橢球為中心的空間直角坐標的變化和橢球參數的變化來表示。這樣建立的關係是三維的，而且比較簡捷，今後已廣泛使用。

橢球定位時，一般都使橢球的短軸平行於地球的平自轉軸，但這種平行關係是由拉普拉斯方位角條件來保證的，而實測的天文方位角總是帶有一定的誤差。因此，不同的空間大地坐標系的三軸之間不可能完全平行，總是存在著微小的差異，而形成一個角度，這個角度稱為歐拉角。在進行大地坐標系的換算時，應顧及歐拉角的影響。如果兩大地坐標系中所使用的尺度不一致，還應顧及由此引起的差異。

大地控制網在平面上計算和平差，要比在橢球面上簡單得多。因此，當區域不大時，可將橢球面上的幾何元素歸算到平面上，然後進行平面上的計算和平差，並將所得的平面坐標直接用於測圖。為此，必須採用某種投影法來建立大地點在橢球面上的大地坐標與其平面直角坐標之間的嚴密的數學關係。滿足大地測量要求的投影法，稱為大地測量投影。

由於橢球面是一個不可平展的曲面，投影時必然要產生投影變形，不可能要求橢球面上圖形的形狀和面積以及兩點間的距離和方向投影后都保持不變。在選擇投影法時，要求採用投影變形小，計算公式簡單的投影法。現代大地測量都採用正形投影法，數學上稱為保角映射或保形映射。橢球面上的無窮小圖形經過投影后，其形狀保持不變。中國在1949年以前採用蘭伯特圓錐投影，此後，改用高斯-克呂格爾投影。兩者都是正形投影。

研究在廣大地面上建立國家大地控制網，測定地球形狀、大小和重力場的理論、技術與方法的科學。測量學與地球物理學相互交叉的學科。它以地球和空間星球為測量對象。

在17世紀以前，大地測量只是處於萌芽狀態，但是人類對於地球形狀的認識有了較大的突破。繼牛頓 (I.Newton，1642～1727) 於1687年發表萬有引力定律之後，荷蘭的惠更斯(C.Huygens，1629～ 1695) 於1690年在其著作《論重力起因》中，根據 地球表面的重力值從赤道向兩級增大的規律，得出地球的外形為兩極略扁的論斷。1743年法國的克萊洛發表了《地球形狀理論》，提出了克萊洛定律。惠更斯和克萊洛的研究為物理學觀點研究地球形狀奠定了理論基礎。隨後又有望遠鏡、測微器、水準器等的發 明，測量儀器精度大幅度地提高，為大地測量學的發展奠定了技術基礎。因此可以說大地測量學是在17 世紀末葉形成的。到了20世紀中葉，幾何大地測量 學和物理大地測量學都已發展到了相當完善的程度。但是，由於天文大地測量工作只能在陸地上實施，無法跨越海洋；重力測量在海洋、高山和荒漠地區也僅 有少量資料，因此對地球形狀和地球重力場的測定都未得到滿意的結果。直到1957年第一顆人造地球衛星發射成功之後，產生了衛星大地測量學，才使大地測量學發展到一個嶄新的階段。在人造衛星出現后的 不長時間內，利用衛星法就精密地測定了地球橢球的 扁率。而且不少國家在地面建立了衛星跟蹤站，從而為建立全球大地坐標系奠定了基礎。此外，利用衛星 雷達測高技術測定海洋大地水準面的起伏也取得了很好的成果；利用發射至月球和行星的航天器，成功地 測定了月球和行星的簡單的幾何參數和物理參數。衛星大地測量學仍在發展中，並且有很大的潛力。

大地測量學的主要研究內容：①常規大地測量學。包括三角測量、導線測量、水準測量、天文測 量、重力測量、慣性測量、橢球面大地測量、地球形 狀理論和測量平差計算；②衛星大地測量學。它是采 用在地面上測定宇宙空間的人造衛星位置的方法來解決大地測量學的問題，即以衛星大地測量幾何法來建立衛星大地網，作為國家基本控制網的高一級控制，或直接建立全球衛星大地網，求定測站點的大地坐標；以衛星大地測量動力法來推求固定的和隨時間變化的地球引力場參數，確定地球形狀和大小、大地水準面差距、重力異常、垂線偏差和地心坐標等。其特點是：視野寬廣，覆蓋面大，速度快，精度高；受大氣折光和垂線偏差影響小，可全天候觀測；各測站之間無需通視，邊長不受通視條件限制；建立全球地心坐標系，避免常規大地測量數據的兩重性和局部性。電子計算技術廣泛用於測量平差計算及大地測量計算以後，不僅解決了大規模數據的嚴密平差計算問題，而且對測量計算的方法也產生了影響。過去按最小二乘法平差，要求各觀測數據是獨立的，現在平差可以考慮相關數據。

亦稱天文大地測量學。經典大地測量學的主要分支。是研究用幾何法測定地球形狀和大小以及地面點幾何位置的學科。它採用一個同地球外形最為接近的旋轉橢球代表地球形狀，用天文大地測量方法測定該橢球的形狀和大小，並以它的表面為參考面，研究和測定大地水準面，建立大地坐標系和推算地面點的幾何位置。

地面點幾何位置的測定包括水平控制測量和高程式控制制測量兩部分。水平控制測量的基本方法有三角測量、邊角測量和導線測量等；高程式控制制測量方法有水準測量和三角高程測量等。分別用於建立一個國家的水平和高程式控制制網。