多重線性代數
多重線性代數
多重線性代數線性代數的一個分支。它以建立在若干個線性空間的笛卡兒積上的各種多重線性的代數結構,例如張量代數、外代數、克利福德代數等為研究對象。多重線性代數在量子力學、群表示論、幾何學、偏微分方程等學科中已有重要的應用。
目錄
線性代數的一個分支。它以建立在若干個線性空間的笛卡兒積上的各種多重線性的代數結構,例如張量代數、外代數、克利福德代數等為研究對象。多重線性代數在量子力學、群表示論、幾何學、偏微分方程等學科中已有重要的應用。
設V1,V2,…,Vr與L都是域F上的線性空間,xj在Vj中。由全體有序r元組(x1,x2,…,xr)組成的集合,稱為V1,V2,…, Vr的笛卡兒積,記作
若關於每一個變元都是線性的,即對於都有
式中;,,則φ稱為從到L的r重線性映射。時,φ 稱為雙線性映射;時,φ統稱為多重線性映射。當,則φ 稱為r重線性函數。
線性空間的張量積 若V1、V2都是域 F上的線性空間,對V1中的每一個基元素ei與V2中的每一個基元素ƒj定義一個積,記為ei圱ƒj,要求這個積是雙線性的,即對ei與ƒj都是線性的。
這些積線性生成F上的一個線性空間,稱為V1與V2的張量積,記為。也可以按如下的辦法用商空間的語言來具體地描述它。令,堸為V生成的自由向量空間,即。在這裡,V中的元素都是堸 的基元素,因此V與堸 的運算不同。N 由堸 中形如與的元素全體線性生成,式中xj,yj在Vj中,α1、α2、b1、b2在F中,則N 是堸 的子空間。作商空間。由 定義的映射,是一個線性同態,稱之為堸 到堸/N 的標準(自然)同態。堸/N稱為V1與V2的張量積,記為V1圱V2。而將記為x1圱x2,讀作“x1與x2的張量積”。x1圱x2生成V1圱V2,其運算圱滿足如下關係:xj,yj均在Vj中α在F中,,,=。因此,由定義的φ:是雙線性映射。注意π與φ的定義域是不同的。可以證明,φ與V1圱V2一起具有如下的泛性質:若L為域F上任一線性空間,為雙線性映射,則有惟一的線性映射使,即有可換圖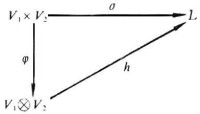 。
。

多重線性代數
也可用泛性質來定義張量積。所謂域 F上兩個線性空間V1與V2的張量積,是指域F上的線性空間T及確定的雙線性映射具有如下的性質:若對於F上的任意線性空間L與任一個雙線性映射都有惟一的線性映射h:T→L使hφ =σ。因為線性空間V1與V2的張量積是由一個線性空間 T和一個確定的雙線性映射 φ組成的,所以有時將張量積記為(T,φ)對或T。上述的(堸/N,π)構作法說明了(T,φ)的存在性。可以證明, 在同構意義下,上述定義的張量積是由V1和V2惟一確定的。仍以x1圱x2記V1圱V2記T。一切形如x1圱x2的元素線性生成V1圱V2,的充分必要條件是x1、x2中至少有一個為0。當V1與V2均為有限維時,可以證明:①dimV2若 {ei}與{ƒj}分別為V1與V2的基底,則{ei圱ƒj}就是V1圱V2的基底。②若V姈與V娦也
是F上的線性空間,,j=1,2,均是線性映射, 由 定義的線性映射,記為ƒ1圱ƒ2,則。③若 V徿也是F上的線性空間,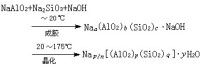 也是線性映射,,則有合成律:,且 I揊圱I揋是 V1圱V2 上的恆等映射。④關於ƒ1圱ƒ2的像與核有性質:
也是線性映射,,則有合成律:,且 I揊圱I揋是 V1圱V2 上的恆等映射。④關於ƒ1圱ƒ2的像與核有性質:

多重線性代數
域F上r個線性空間V1,V2,…,Vr的張量積也可用泛性質定義如下:若V為F上的線性空間,×是r重線性映射, 對於 F上的任一線性空間V┡與任一個r重線性映射,都有惟一的線性映射h:V→V┡使,則(V,φ)或V稱為V1,V2,…,Vr的張量積,記為V1圱V2圱…圱Vr。記為x1圱x2圱…圱xr。類似於r=2的情形,可以證明它的存在性和在同構意義下的惟一性,以及在同構意義下張量積運算具有結合性。當 均為有限維時,則dim(V1圱V2圱…圱Vr。
張量代數 設 V是域F上的線性空間,圱rV表r個V的張量積,稱為V 的r 次張量冪。若{e1,e2,…,en}是V的基底,則 圱rV 的基底為{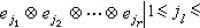 r}有 nr個元素。圱rV 的元素T 總可表為
r}有 nr個元素。圱rV 的元素T 總可表為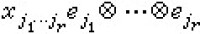 ,並稱為r階張量。式中的nr個純量∈F,稱為張量T關於V的基底的分量。
,並稱為r階張量。式中的nr個純量∈F,稱為張量T關於V的基底的分量。
多重線性代數
多重線性代數
約定圱1V=V,圱0V=F,於是是F上的線性空間,每一個圱rV 都是它的子空間,這裡嘰表直和。將圱V中生成元的乘法定義為
式中xj、yj∈V,經線性開拓即得圱V 中完全確定的乘法,使之成為F上的一個有單位元的結合代數,即所謂V上的張量代數。它具有如下的泛性質:若τ:V→圱V 是標準單射(嵌入),A是F上任一個有單位元的結合代數,σ:V→A是線性映射,則有惟一的代數同態φ:圱使φτ=σ。這個泛性質也可用來定義圱V。此時,它的存在性已由它的具體構造法證明,而它在同構意義下的惟一性的證明與張量積的惟一性證明相仿。這個泛性質蘊含如下性質:若也是F上的線性空間,則每一個線性映射ƒ1:V →都惟一地誘導一個代數同態使,且,式中1表恆等映射。對於F上的三個線性空間V、、,則由線性映射:→的合成ƒ2ƒ1誘導的代數同態,即與ƒ→T(ƒ)確定了一個從F上的線性空間範疇到 F上有單位元的結合代數範疇的一個共變函子。(見範疇)
若V*為V 的對偶空間,則r個V*與s個V的張量積,記為圱V,其元素稱為r階共變、s階反變的階混合張量,當時,圱V 即為圱rV*,其元素稱為r階共變張量;當r=0時,圱V 即為圱V,其元素稱為 s階反變張量;圱姲V即V*;圱嬼V 即V;圱孊V 即F。若為V 的基底,與相應的對偶基即,式中δijnr+s個元素,形成圱V 的基底。圱V 的每一個元素都可惟一地表為的形式,其中的nr+s個純量
,稱為(混合)張量T對於V的基底的分量。仿圱V 的構作可得混合張量代數。它也是F上的線性空間,因此,張量的加法與純量乘法都可歸為對分量的運算,還可推出張量乘法的分量公式。
如果V是F上的具有內積( ,)的內積空間,那麼定義圱rV 的內積為
,
式中xj、yj均在V中,j=1,2,…,r,圱rV 就成為F上的內積空間。若{e1,e2,…,en}為V的法正交基即(時,也是圱rV 的法正交基。還可將這個內積開拓到作為線性空間的圱V上,即若 ,式中Tr、Sr均在圱rV 中,則T與S的內積定義為
此時可以證明,若,則 g與V 的法正交基的選取無關。g稱為V的反變度量張量。對V*的對偶基可類似地定義共變度量張量g*。此時可證,只要V的基底{ƒj}與V*的基底{ƒk}為對偶基(未必是法正交基),那麼g與g*總可表為 ,。
由張量代數可派生出兩個重要的代數即外代數與對稱張量代數。它們是兩個平行的分支。
外代數 亦稱格拉斯曼代數或反對稱張量代數。設V為域F上的線性空間,F的特徵為0,Nr(V)表示圱rV中由形如x1圱x2圱…圱xr的元素全體(其中存在當的情形)生成的子空間,φ為V×…×V到F上的線性空間的r 重線性映射,σ為任一r元置換,由定義σφ ,式中。由定義的πA,稱為交代化子,式中的εσ,當 σ為偶置換時為1;否則,為-1。易知。商空間圱rV/Nr(V)稱為V 的r次外乘冪,記為∧rV,它的元素x1圱x2圱…圱xr+Nr(V),則以x1∧x2∧…∧xr記之。仿照由張量冪作直和構造出張量代數的方法,取,其中約定,於是∧V也是F上的線性空間。在∧V中定義生成元的乘法為,,經過線性開拓即得∧V中的乘法,並使∧VV上的外代數。它不是可交換代數,它的乘法滿足如下的規則:,式中x在∧rVy在∧sV中。因此,對於V中的x有x∧x=0,但x不在V中時,x∧x未必為0。
當{e1,e2,…,en}為V 的基底時,易證是∧rV 的基底,因此r≤n時,而 r>n 時dim∧rV=0。於是,式中表從n個元素中取r個元素的組合數。若V是具有內積( ,)的內積空間,則可由 作線性開拓來定義∧V中的內積,式中xj與yj均在V中,使∧V成為F上的內積空間。
也可用泛性質來定義外代數。設K是域F上的一個有單位元的結合代數,F的特徵為0,V是F上的線性空間,τ:V→K 是任一線性映射,且滿足條件:①(τx)2=0,其中x∈V;②苦A是 F上任一有單位元的結合代數,σ:V→A是任一線性映射,且使(σx)2=0,其中x∈V,則必有惟一的代數同態 φ:K→A使φτ=σ。此時(K,τ) 對或K就稱為V上的外代數,記為 E=∧V。可以證明其存在性及其在同構意義下的惟一性,證法與張量代數類似。K中的元素又稱為 V上的反對稱張量。外代數可以概括行列式理論。外代數的推廣就是克里福特代數,它也是一種有重要應用的代數,用它可將複數、四元數代數概括在內。
若V*是V的對偶空間,則與構成混合張量代數類似,可將 ∧V*圱∧V 記為∧(V*,V),由=, 式中x、y∈V,x、y∈V,作線性開拓來定義∧(V*,V)的乘法,使∧(V, V)成為有單位元的結合代數,而稱其為V上的混合外代數。
對稱張量代數 它的理論及構作法是與外代數平行的。可以用來定義關於r重線性映射的對稱化子,令。稱為V的r次對稱冪,記為∨rV,約定,記,式中嘰表直和。仿照前面來定義其乘法運算,即可得V上的對稱張量代數。它也可用泛性質給以定義,設S為域F上有單位元的結合代數,F的特徵為0,V 是F上的線性空間,τ┡:V →S 是線性映射,且滿足條件:①,② 當 A是 F上任一個有單位元的結合代數,σ┡:V →A 是任一線性映射,且滿足,這裡x1,x2均在V中,則必有惟一的代數同態 φ┡:S→A使φ┡τ┡=σ┡。此時(S,τ┡)對或S稱為V上的對稱張量代數,記為 S=∨V,其元素稱為V上的對稱張量。對稱張量代數概括了通常的多元多項式代數。當dimV=n時,V上的對稱張量代數等價於F上關於n個文字x1,x2,…,xn的多項式環,即∨。對稱張量代數的許多結果都可與外代數的相應結果平行地建立起來。
參考書目
W. H. Greub,Multilinear Algebra, 2nd ed.,SpringerVerlag,New York,1978.