商空間

在近世代數，群理論中有商群的概念，環理論中有商環的概念. 類似地，在線性空間理論中我們可以有商空間的概念. 在拓撲學及其相關數學領域，一個商空間（quotient space，也稱為等化空間 identification space）直觀上說是將一個給定空間的一些點等同或“黏合在一起”；由一個等價關係確定哪些點是等同的。這是從給定空間構造新空間的常見方法。

假設 X 是一個拓撲空間，~ 是 X 上一個等價關係。在商集合 X/~ （這個集合有所有 ~ 的等價類組成）上定義一個拓撲如下：X/~ 中一個等價集合是開集當且僅當他們的並集在 X 中是開集。所得的拓撲稱為在商集合 X/~ 上的商拓撲（quotient topology）。

等價地，商拓撲可以如下方式刻畫：設 q : X → X/~ 是投影映射，將 X 的任何元素映為它的等價類。則 X/~ 上的商拓撲是使 q 連續的最細拓撲（finest topology）。

給定一個滿射 f : X → Y 從一個拓撲空間 X 到一個集合 Y，我們可以在 Y 上定義商拓撲為使 f 連續的最細拓撲。這等價於說集合 V ⊆ Y 在 Y 中開當且僅當它的原像 f−1(V) 在 X 中開。映射 f 在 X 上誘導了一個等價關係，即 x1~x2 當且僅當 f(x1) = f(x2)。這個商空間 X/~ 同胚於 Y（帶著它的商拓撲），同構映射為將 x 的等價類映為 f(x)。

一般地，一個滿連續映射 f : X → Y 稱為一個商映射（quotient map）如果 Y 具有由 f 確定的商拓撲。

黏合：通常，拓撲學家討論將一些點黏合在一起。如果 X 是一個拓撲空間，點“黏合”在一起，這意味著我們考慮由等價關係 a~b 當且僅當 a = b 或 a = x，b = y（或 a = y，b = x）得到的商空間。即這兩個點被看作一個。考慮一個單位正方形 I2 = [0，1]×[0，1] 以及由所有邊界點等價生成的等價關係 ~ ，從而所有邊界點等同到一個等價類。則 I2/~ 同構於單位球面 S2。黏著空間（Adjunction space）：更一般地，假設 X 是一個空間，A 是 X 的一個子空間。我們可以將 A 中所有點等同到一個等價類其餘 A 以外的點不變。所得的空間記作 X/A。

2 維球面同構於將單位圓盤的邊界等同為一個點 D2/∂D2。

考慮集合 X = R'，取通常拓撲的實數集，記 x ~ y 當且僅當 x−y 是一個整數。則商空間 X/~ 同構於單位圓周 S1，同構映射為將 x 的等價類映為 exp(2πix)。

上一個例子的一類大量的推廣如下：假設一個拓撲群 G 連續作用在空間 X 上。我們可以構造 X 上一個等價關係，如果兩點等價當且僅當它們在同一個軌道中。這個關係下的商空間稱為軌道空間，記作 X/G。上一個例子中 G = Z 通過平移作用在 R 上。軌道空間 R/Z 同構於 S1。

註：記號 R/Z 有歧義：如果 Z 理解成一個群作用在 R 上則商空間是圓周；如果 Z 看作 R 的一個子空間，則商空間是無窮的一束圓（bouquet of circles）在同一個點聯接起來。

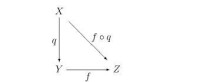
商映射 q : X → Y 是由如下性質刻畫的滿射：如果 Z 是任何拓撲空間，f : Y → Z 是任何函數，則 f 連續當且僅

當 f O q 連續。

商空間 X/~ 與商映 q : X → X/~ 一起由如下泛性質刻畫。如果 g : X → Z 是一個連續映射使得：對所有 a 與 b 屬於 X， a~b 蘊含 g(a)=g(b) ，則存在惟一連續映射 f : X/~ → Z 使得 g = f O q。我們稱 g “下降到商”。

因此定義在 X/~ 商的連續映射恰是由定義在 X 上與等價關係一致的連續映射（它們將同一個等價類中的元素映到相同的像）誘導的。在研究商空間時，時常使用這個判據。

給定一個連續滿射 f : X → Y，關於 f 是否為商映射的判據是有用的。兩個充分條件是 f 為開映射或閉映射。注意這兩個條件只是充分條件而不是必要的。容易構造出不開或不閉的商映射例子。

與其它拓撲概念的相容性

分離

一般地，商空間關於分離公理的表現都很壞。X 的分離性質不必被 X/~ 繼承，而 X/~ 可能具有 X 所沒有的分離性質。

X/~ 是一個T1空間當且僅當 ~ 的任何等價類在 X 中閉。

如果商映射開則 X/~ 是一個豪斯多夫空間當且僅當 ~ 是乘積空間 X×X 的一個子集。

如果一個空間是連通的或道路連通，則所有的商空間也是。

一個單連通或可縮空間的商空間不必具有同樣的性質。

緊性

如果一個空間緊，則所有商空間也是。

一個局部緊空間的商空間不必是局部緊的。

一個商空間的拓撲維數可能比原空間大（顯然也可能比較小），皮亞諾曲線（space-filling curve）提供了這樣的例子。

應用線性空間的第二同構定理，我們可得線性代數中的一個著名維數公式.

定理3.1 設W1，W2是有限維線性空間V的兩個子空間，則 dim（W1＋W2）＝dimW1＋dimW2－dim（W1∩W2）.證明：由定理2.7，（W1＋W2）∕W2≌W1∕（W1∩W2），於是dim（（W1＋W2）∕ W2）＝dim（W1∕（W1∩W2））. 由命題1.3知dim（W1＋W2）－dim W2＝dimW1－dim（W1∩W2）.

應用線性空間的同態基本定理，我們可得線性代數中的另一個著名的維數公式.

定理3.2 設f是數域P上線性空間V到V’的同態映射，dimV＝n，則 dim ker f＋dim Im f ＝n .

證明：由推論2.6，Im f ≌V∕kerf，於是dim Im f＝dim（V∕ker f）.由命題1.3，可得

dim Im f ＝n－dim ker f.

註：定理3.1與3.2用傳統的方法（參見一些高等代數、線性代數教材）來證明則比較繁雜，在這裡我們看到，它們本質上是第一、二同構定理的直接推論.

定理3.2有兩個有用的推論：

推論3.3 設V是數域P上有限維線性空間，σ、τ是V上的自同態（線性變換），則 dim Im（στ）＝dim Im（τ）－dim（Im（τ）∩ker（σ））.

證明：將σ限制在子空間Im（τ）上，知σ| Im（τ）是Im（τ）到V的一個同態映射，由定理3.2，

dim（ker（σ）∩Im（τ））＋dim Im（στ）＝dim Im（τ）.

推論3.4 設A, B是數域P上m×n, n×M矩陣，則 r（AB）＝ r（B）－dim（R（B）∩N（A）） ＝ r（A）－dim（R（AT）∩N（BT））這裡R(B)＝{X | BY＝X，Y∈PS}，N(A)＝{X | AX＝0，X∈Pn}是Pn的子空間，r（A）為A的秩.

證明：將A限制在子空間R(B)上，則A可看成R(B)到R(A)的一個同態映射，其像為R(AB)，核為R(B)∩N(A)，於是由定理3.2，

dim（R（B）∩N（A））＋dim R（AB）＝dim R（B）.

由於dim R（AB）＝r（AB），dim R（B）＝r（B），故有：

r（AB）＝r（B）－dim（R（B）∩N（A））.……………………（*）

因為r（AB）＝r（（AB）T）＝r（BT AT），r（A）＝r（AT），將BT AT應用到（*）式，可得：

r（AB）＝r（A）－dim（R（AT）∩N（BT））.

利用推論3.3和3.4，可證明一些著名不等式.

例1 證明Sylvester不等式

r（A）＋r（B）－n≤r（AB）≤min{ r（A），r（B）}，

其中A為n列，B為n行.

證明：由推論3.4，有r（AB）＝r（B）－dim（R（B）∩N（A））. 因為n－r（A）＝dim N(A)≥dim（R（B）∩N（A））≥0，所以

r（AB）＝r（B）－dim（R（B）∩N（A））

≥r（B）－（n－r（A））

＝r（A）＋r（B）－n.

又由推論3.4，顯然有r（AB）≤r（B），r（AB）≤r（A）.

例2 證明Frobenius不等式

r（ABC）≥r（AB）＋r（BC）－r（B）.

證明：由推論3.4，

r（ABC）＝r（BC）－dim（R（BC）∩N（A）），

r（AB）＝r（B）－dim（R（B）∩N（A）），

兩式相減得：

r（ABC）＝r（AB）＋r（BC）－r（B）＋dim（R（B）∩N（A））－dim（R（BC）∩N（A））.因為R（BC） R（B），所以dim（R（B）∩N（A））－dim（R（BC）∩N（A））≥0，因此

r（ABC）≥r（AB）＋r（BC）－r（B）.

例3 設σ，τ都是數域P上n維線性空間V上的線性變換，證明

dim ker（στ）≤dim ker（σ）＋dim ker（τ）.

證明：由定理3.2及推論3.3，

dim Im（στ）＝dim Im（τ）－dim（Im（τ）∩ker（σ）），

dim Im（στ）＋dim ker（στ）＝n，

dim Im（τ）＋dim ker（τ）＝n。

於是，有

dim ker（στ）＝dim ker（τ）＋dim（Im（τ）∩ker（σ））。

≤dim ker（τ）＋dim ker（σ）。

例4 設σ是數域P上n維線性空間V上的線性變換，證明

dim Im（σ2）＝dim Im（σ）當且僅當Im（σ） ker（σ）＝V。

證明：由推論3.3，dim Im（σ2）＝dim Im（σ）－dim（Im（σ）∩ker（σ）），於是dim Im（σ2）＝dim Im（σ）當且僅當dim（Im（σ）∩ker（σ））＝0，當且僅當Im（σ）∩ker（σ）＝{0}。又由定理3.2，dim Im（σ）＋dim ker（σ）＝n，故可得dim Im（σ2）＝dim Im（σ）當且僅當Im（σ） ker（σ）＝V。

[1] 教學網 http://gdjpkc.xmu.edu.cn/Document/Q2006120805530978471.doc