多目標規劃
多目標規劃
多目標極小化問題通常記為(VMP)
,
其中 是給定的一個向量值目標函數,T表示轉置,表示在區域 X上的函數ƒ1(x),ƒ2(x),…,ƒm(x)被同等地極小化。
若(VMP)中的ƒ(x)是x的線性(向量)函數,X是R中的多面體,則相應的問題稱為多目標線性規劃問題。若(VMP)中的ƒ(x)是x的非線性(向量)函數,或X不是R中的一個多面體,則稱為多目標非線性規劃問題。對於多目標規劃,解的定義是一個非常重要的問題。
有效性 亦稱帕雷托最優性,有時也稱為非劣性或非受控性或可採納性,是T.C庫普曼斯於1951年引入的。命名為帕雷托最優性是為了紀念法國經濟學家V.帕雷托首先提出多目標最優化的思想。由於向量序不是完全序,因而對於問題(VMP)一般不存在x∈X使所有的ƒi(x)(i=1,2,…,m)同時達到極小。因此,單目標問題的最優解概念在這裡已不適用,而代替它的則有有效解、弱有效解和非劣解等概念。如果∈X,且不存在其他的可行點x使得ƒ(x)≤ƒ(),則稱為(VMP)的有效解(這裡“≤”表示向量的每一分量間都是“≤”且至少有一個分量間是“<”,而“<”表示它們的每一個分量間都是“<”)。有效解也叫做帕雷托最優解或非劣解。如果塣∈X, 且不存在其他的可行點x使ƒ(x)<ƒ(),則稱為(VMP)的弱有效解。設ƒ把X映射到R中的可達目標集Y=ƒ(X)。若Y是一緊集,則問題(VMP)的有效解和弱有效解存在。
一個多目標規劃問題通常存在許多個有效解。在自然序意義下,因各有效解之間相互不能進行比較。因而要在它們之中加以選擇,就需要引入一個偏愛序。這相當於要從決策者那裡得到另外的信息。如何選取這種另外的信息以提煉成一種偏愛模式,並且在某種偏愛關係的基礎上建立起有關的數學理論,是多目標規劃研究的一個重要課題。
1968年A.M.日夫里翁引進了真有效解概念:如果是(VMP)的有效解,且存在一數值M>0,使得對於滿足ƒi(x)<ƒi()的每一i和每一x∈X,至少存在一個使 ƒi(x)>ƒ(j)的j(1≤j≤m)有【ƒi()-ƒi(x)】/【ƒj(x)-ƒj()】≤M,則稱為問題(VMP)的真有效解。在多目標規劃的研究中,還引入了一些其他意義下的解的概念,如局部有效解、庫恩-塔克爾意義下的有效解等。對這些解的性質及其相互關係已進行了若干探討,例如,對偽單調多目標規劃、凸多目標規劃已研究了有效解的性質,並建立了一些關於有效解和弱有效解的判別準則。在多目標規劃的研究中,目標空間並不限於歐氏空間R,例如,目標函數是表示一國經濟增長的一個動態模型的所有軌線,則目標空間就是一個希爾伯特空間。目前,目標空間是抽象的巴拿赫空間或希爾伯特空間的情形,已有不少研究。
一個與多目標問題(VMP)相關聯的單目標問題(Pλ)
是引人重視的,其中λi叫做權係數,叫做權向量。通常要求權係數滿足或‖λ‖=1(依R中任意選定的模)使之規範化。記,,則有以下的基本定理:
設∈X是(Pλ)的最優解,λ∈Λ,則是(VMP)的弱有效解;若X是凸集,ƒ(x)是X上的凸函數,且是(VMP)的弱有效解,則存在某一λ∈Λ使是(Pλ)的最優解。若λ∈Λ,是(Pλ)的最優解,則是(VMP)的真有效解;若X是凸集,ƒ(x)是X上的凸函數,且是(VMP)的真有效解,則存在某一λ∈Λ使是(Pλ)的最優解。
通過帶權係數的問題(Pλ),可以把非線性規劃的許多結果移置到多目標規劃中來。權係數是一種類型的拉格朗日乘子,利用線性泛函來分離集合的一切理論都可用於此處。對無限維的情形,對鞍點和對偶定理都可進行研究。從計算方法上來說,求(VMP)的有效解或弱有效解,可歸為求參數規劃問題 (Pλ)的最優解。當λ遍跡Λ 或Λ時,將產生所有的有效解或弱有效解。但是,對於(VMP)的一個給定的有效解或弱有效解,選擇一個適當的權向量λ並非易事。這是用權係數求解的弱點。
以下定理在實用中可以檢驗一個點的有效性,並用來產生一個有效解或判定問題的有效解不存在。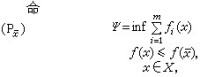 其中塣是X中的一個給定點。①塣是 (VMP)的有效解的充分必要條件為塣是(P)的最優解。②若Ψ是有限的,並且∈X是(P?/I>)的最優解,則是(VMP)的有效解。③若X是凸集,ƒ(x)是 X上的凸函數,問題(P)無有限的最小值存在,則(VMP)不存在真有效解。這些結果是R.E.溫德爾和D.N.李於1977年得到的。
其中塣是X中的一個給定點。①塣是 (VMP)的有效解的充分必要條件為塣是(P)的最優解。②若Ψ是有限的,並且∈X是(P?/I>)的最優解,則是(VMP)的有效解。③若X是凸集,ƒ(x)是 X上的凸函數,問題(P)無有限的最小值存在,則(VMP)不存在真有效解。這些結果是R.E.溫德爾和D.N.李於1977年得到的。
多目標規劃
1978年,H.P.本森給出有效解與真有效解之間關係的一個結果:設ƒ(x)是凸集X上的凸函數,S={s∈R|s≤ƒ(x)對某一x∈X成立}是閉集,則任意非真有效解必是某一真有效解序列的極限。此外,用K表示所有有效解的集合,Kp表示所有真有效解的集合,若ƒ(x)在閉凸集X上是連續的和凸的,則有關係 ,其中一橫表示閉運算。
1.化多為少的方法,即把多目標規劃問題歸為單目標的數學規劃(線性規劃或非線性規劃)問題進行求解,即所謂標量化的方法,這是基本的演演算法之一。
① 線性加權和法 對於多目標規劃問題(VMP),先選取向量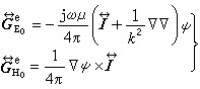 ,要求λi>0(i=1,2,…,m)和,作各目標線性加權和,然後求解單目標數學規劃問題
,要求λi>0(i=1,2,…,m)和,作各目標線性加權和,然後求解單目標數學規劃問題
多目標規劃
, (1)
設是問題(1)的最優解,則可以證明是問題(VMP)的有效解。若選取向量λ≥0,則相應的問題(1)的最優解是多目標規劃問題(VMP)的弱有效解。向量λ的各個分量λi(i=1,2,…,m)通常叫做權係數。它的大小反映了各相應分目標在問題中的重要程度。一般,對權係數的不同選取,可以得到問題(VMP)的不同的有效解或弱有效解。如何選取權係數,對於不同的問題可以有不同的處理方法。
② 理想點法 為了求解多目標規劃問題(VMP),先依次極小化各個分目標。設求得第 i個目標的極小值 ,則得到R中的一個點
,則得到R中的一個點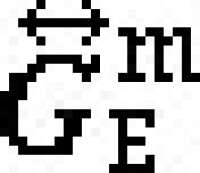 。由於點ƒ
。由於點ƒ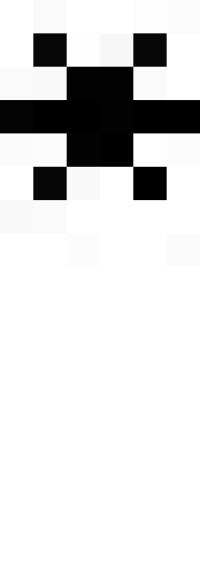 的各個分量對於相應的分目標而言是最理想的值,故稱ƒ
的各個分量對於相應的分目標而言是最理想的值,故稱ƒ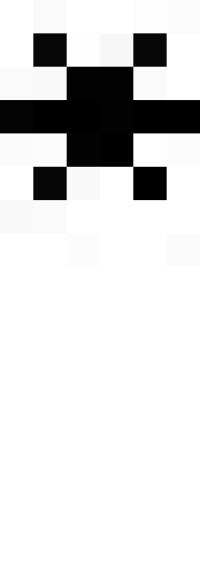 為問題(VMP)的理想點。選取權係數λi>0(i=1,2,…,m),並作偏差(函數)
為問題(VMP)的理想點。選取權係數λi>0(i=1,2,…,m),並作偏差(函數)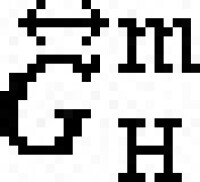 ,最後求解數學規劃問題
,最後求解數學規劃問題
多目標規劃
多目標規劃
多目標規劃
多目標規劃
多目標規劃
。 (2)
問題(2)的最優解是問題(VMP)的有效解。理想點法的基本思想是在某種意義下使向量目標函數與所考慮問題的理想點的偏差為極小,來求出多目標規劃問題的有效解。在上述偏差中,p的不同取值代表了不同意義的偏差。當取p=2,λi=1(i=1,2,…,m),則偏差就為距離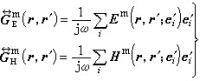 。這種情形,理想點法也叫做最短距離法。
。這種情形,理想點法也叫做最短距離法。
多目標規劃
2. 分層求解法 對於問題(VMP),假若目標函數 的各個分目標可以按其在問題中的重要程度排出先後次序,並設這個次序為:ƒ1(x),ƒ2(x),…,ƒm(x)。先對第一個目標進行極小化: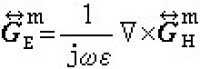 ,設得到的最優解為x。然後,按下述格式依次分層對各目標進行極小化:
,設得到的最優解為x。然後,按下述格式依次分層對各目標進行極小化:
多目標規劃
(3)
式中。設k=m時得到問題(3)的最優解x,則在每一的條件下,x是多目標規劃(VMP)的有效解。在實用中,為了保證每一,常把上述Xk中的等式約束作適當的寬容,即給出一組所謂寬容量 δi(i=1,2,…,m-1),並以代替 (3)中的Xk。在δi>0的條件下,由k代替Xk所得到的x是多目標規劃(VMP)的弱有效解。
3.其它方法
對多目標的線性規劃除以上方法外還可以適當修正單純形法來求解;還有一種稱為層次分析法,是由美國運籌學家沙旦於70年代提出的,這是一種定性與定量相結合的多目標決策與分析方法,對於目標結構複雜且缺乏必要的數據的情況更為實用。
多目標最優化思想,最早是在1896年由法國經濟學家V.帕雷托提出來的。他從政治經濟學的角度考慮把本質上是不可比較的許多目標化成單個目標的最優化問題,從而涉及了多目標規劃問題和多目標的概念。1947年,J.馮·諾伊曼和O.莫根施特恩從對策論的角度提出了有多個決策者在彼此有矛盾的情況下的多目標問題。1951年,T.C.庫普曼斯從生產和分配的活動中提出多目標最優化問題,引入有效解的概念,並得到一些基本結果。同年,H.W.庫恩和A.W.塔克爾從研究數學規劃的角度提出向量極值問題,引入庫恩-塔克爾有效解概念,並研究了它的必要和充分條件。1963年,L.A.扎德從控制論方面提出多指標最優化問題,也給出了一些基本結果。1968年,A.M.日夫里翁為了排除變態的有效解,引進了真有效解概念,並得到了有關的結果。自70年代以來,多目標規劃的研究越來越受到人們的重視。至今關於多目標最優解尚無一種完全令人滿意的定義,所以在理論上多目標規劃仍處於發展階段。
參考書目
A.M.Geoffrion, Proper Efficiency and the Theory of Vector Maximization,Jaurnal of MatheMatical Anal ysis and Applications,22,1968.
H.P.Benson, Existence of Efficient Solutions for Vector Maximization Problems,Jaur.,Opti.Theory Appl.26,4,1978.
C.L.Paid Hwang and A. S. M. Masnd,Multiple Objective Decision Making-method and Application(Lecture Notes in Economics and MatheMatical Systems), Springer Verlag, Berlin, 1979.