多目標線性規劃
多目標線性規劃
多目標最優化思想,最早是在1896年由法國經濟學家V.帕雷托提出來的。他從政治經濟學的角度考慮把本質上是不可比較的許多目標化成單個目標的最優化問題,從而涉及了多目標規劃問題和多目標的概念。1947年,J.馮·諾伊曼和O.莫根施特恩從對策論的角度提出了有多個決策者在彼此有矛盾的情況下的多目標問題。1951年,T.C.庫普曼斯從生產和分配的活動中提出多目標最優化問題,引入有效解的概念,並得到一些基本結果。同年,H.W.庫恩和 A.W.塔克爾從研究數學規劃的角度提出向量極值問題,引入庫恩-塔克爾有效解概念,並研究了它的必要和充分條件。1963年,L.A.扎德從控制論方面 提出多指標最優化問題,也給出了一些基本結果。1968年,A.M.日夫里翁為了排除變態的有效解,引進了真有效解概念,並得到了有關的結果。自70年代以來,多目標規劃的研究越來越受到人們的重視,多目標規劃仍處於發展階段。
線性規劃是運籌學中研究較早、發展較快、應用廣泛、方法較成熟的一個重要分支,它是輔助人們進行科學管理的一種數學方法。在經濟管理、交通運輸、工農業生產等經濟活動中,提高經濟效果是人們不可缺少的要求,而提高經濟效果一般通過兩種途徑:一是技術方面的改進,例如改善生產工藝,使用新設備和新型原材料。二是生產組織與計劃的改進,即合理安排人力物力資源。線性規劃所研究的是:在一定條件下,合理安排人力物力等資源,使經濟效果達到最好。一般地,求線性目標函數在線性約束條件下的最大值或最小值的問題,統稱為線性規劃問題。滿足線性約束條件的解叫做可行解,由所有可行解組成的集合叫做可行域。決策變數、約束條件、目標函數是線性規劃的三要素。
多目標規劃是數學規劃的一個分支。研究多於一個的目標函數在給定區域上的最優化。又稱多目標最優化。通常記為 MOP。多目標規劃的概念是 1961年由美國數學家查爾斯和庫柏首先提出的。
求解多目標規劃的方法大體上有以下幾種:一種是化多為少的方法,即把多目標化為比較容易求解的單目標或雙目標,如主要目標法、線性加權法、理想點法等;另一種叫分層序列法,即把目標按其重要性給出一個序列,每次都在前一目標最優解集內求下一個目標最優解,直到求出共同的最優解。對多目標的線性規劃除以上方法外還可以適當修正單純形法來求解;還有一種稱為層次分析法,是由美國運籌學家沙旦於70年代提出的,這是一種定性與定量相結合的多目標決策與分析方法,對於目標結構複雜且缺乏必要的數據的情況更為實用。
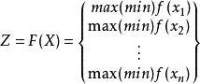
多目標線性規劃
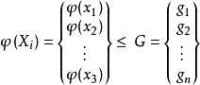
多目標線性規劃
式中X為決策變數向量,如果將上面兩個式子進一步縮寫, , 。其中:是k維函數向量 K是目標函數的個數;G 是m維常數向量;m是約束方程的個數。
對於線性多目標規劃問題,上述式子可以進一步用矩陣表示:
式中X為n維決策變數向量;A為矩陣,即目標函數係數矩陣;B為矩陣,即約束方程係數矩陣;b為m維的向量,約束向量。
多目標線性規劃是多目標最優化理論的重要組成部分,由於多個目標之間的矛盾性和不可公度性,要求使所有目標均達到最優解是不可能的,因此多目標規劃問題往往只是求其有效解(非劣解)。目前求解多目標線性規劃問題有效解的方法,有理想點法、線性加權和法、最大最小法、目標規劃法,模糊數學解法等。為了求得多目標規劃問題的非劣解,常常需要將多目標規劃問題轉化為單目標規劃問題去處理。實現這種轉化,有如下幾種建模方法。
1、效用最優化模型
2、罰款模型
3、約束模型
4、目標達到法
5、目標規劃模型
效用最優化模型(線性加權法)
思想:規劃問題的各個目標函數可以通過一定的方式進行求和運算。這種方法將一系列的目標函數與效用函數建立相關關係,各目標之間通過效用函數協調,使多目標規劃問題轉化為傳統的單目標規劃問題。
罰款模型(理想點法)
思想: 規劃決策者對每一個目標函數都能提出所期望的值(或稱滿意值);通過比較實際值與期望值之間的偏差來選擇問題的解。
約束模型(極大極小法)
理論依據:若規劃問題的某一目標可以給出一個可供選擇的範圍,則該目標就可以作為約束條件而被排除出目標組,進入約束條件組中。假如,除第一個目標外,其餘目標都可以提出一個可供選擇的範圍,則該多目標規劃問題就可以轉化為單目標規劃問題。
目標達到法
首先將多目標規劃模型化為標準形式,在求解之前,先設計與目標函數相應的一組目標值理想化的期望目標與每一個目標對應的權重係數,再設鬆弛因子,對多目標規劃問題進行轉化。
目標規劃模型(目標規劃法)
需要預先確定各個目標的期望值,同時給每一個目標賦予一個優先因子和權係數,假定有K個目標,L個優先順序( ),再通過建立目標規劃模型進行求解。
例1.解圖1所示的多目標線性規劃問題。
解普通線性規劃問題1: 和約束條件,得最優解為 ,, ,最優值為2,此時。
同理,解普通線性規劃問題2:和約束條件,得最優解為 , ,,最優值為20,此時。
同時考慮兩個目標,合理的方案是使 , ,可取伸縮指標分別為, 。如果認為目標 更重要,可單獨縮小;如果認為目標 更重要,可單獨縮小。
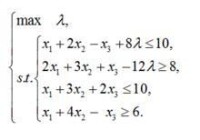
圖2
此時 ,。得最優解為 , , ,。