黃金數

黃金分割數是無理數，前面的10位為：

0.618033988

設一條線段AB的長度為a，C點在靠近B點的黃金分割點上且AC為b

AC/AB=BC/AC

b^2=a×(a-b)

b^2=a^2-ab

a^2-ab+(1/4)b^2=(5/4)×b^2

(a-b/2)^2=(5/4)b^2

a-b/2=（√5/2）×b

a-b/2=(√5)b/2

a=b/2+(√5)b/2

a=b(√5+1）/2

a/b=(√5+1）/2

據傳，這是公元前六世紀古希臘數學家畢達哥拉斯的徒弟希伯斯所發現，後來古希臘哲學家柏拉圖將此稱為黃金分割。這其實是一個數字的比例關係，即把一條線分為兩部分，此時長段與短段之比恰恰等於整條線與長段之比，其數值比為1.618：1或1：0.618，也就是說長段的平方等於全長與短段的乘積。0.618，以嚴格的比例性、藝術性、和諧性，蘊藏著豐富的美學價值。為什麼人們對這樣的比例，會本能地感到美的存在？其實這與人類的演化和人體正常發育密切相關。據研究，從猿到人的進化過程中，骨骼方面以頭骨和腿骨變化最大，軀體外形由於近似黃金而矩形變化最小，人體結構中有許多比例關係接近0.618，從而使人體美在幾十萬年的歷史積澱中固定下來。人類最熟悉自己，勢必將人體美作為最高的審美標準，由物及人，由人及物，推而廣之，凡是與人體相似的物體就喜歡它，就覺得美。於是黃金分割律作為一種重要形式美法則，成為世代相傳的審美經典規律，至今不衰！在研究黃金分割與人體關係時，發現了人體結構中有14個“黃金點”（物體短段與長段之比值為 0.618），12個“黃金矩形”（寬與長比值為 0.618的長方形）和2個“黃金指數”（兩物體間的比例關係為 0.618）。

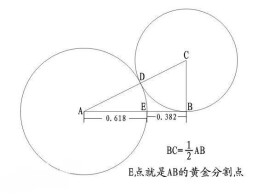
1．設已知線段為AB，過點B作BC⊥AB，且BC=AB÷2；

2．連結AC；

3．以C為圓心，CB為半徑作弧，交AC於D；

4．以A為圓心，AD為半徑作弧，交AB於P，則點P就是AB的黃金分割點。

事實上，在一個黃金矩形中，以一個頂點為圓心，矩形的較短邊為半徑作一個四分之一圓，交較長邊與一點，過這個點，作一條直線垂直於較長邊，這時，生成的新矩形（不是那個正方形）仍然是一個黃金矩形，這個操作可以無限重複，產生無數個黃金矩形。

所謂黃金三角形是一個等腰三角形，其腰與底的長度比為黃金比值；對應的還有：黃金矩形等。

分類

黃金三角形分兩種：

一種是等腰三角形，兩個底角為72°，頂角為36°；這種三角形既美觀又標準。這樣的三角形的底與一腰之長之比為黃金比：(√5-1)/2.

另一種也是等腰三角形，兩個底角為36°，頂角為108°；這種三角形一腰與底邊之長之比為黃金比：(√5-1)/2.

黃金三角形是一個等腰三角形，它的頂角為36°，每個底角為72°.它的腰與它的底成黃金比．當底角被平分時，角平分線分對邊也成黃金比，並形成兩個較小的等腰三角形．這兩三角形之一相似於原三角形，而另一三角形可用於產生螺旋形曲線．

黃金三角形的一個幾何特徵是：它是唯一一種能夠由5個與其全等的三角形生成其相似三角形的三角形。

把五個黃金三角形稱為“小三角形”，拼成的相似黃金三角形稱為“大三角形”。則命題可以理解為：五個小三角形能夠不重疊又不超出地充滿大三角形。要滿足這種填充，必要條件之一是大三角形的每條邊都可以由若干條小三角形的邊相加而成。

根據定義，第一種黃金三角形是腰與底的比值為(√5+1)/2的等腰三角形，頂角為36°，底角為72°。

設小三角形的底為a，則腰為b=(√5+1)a/2，因為大三角形的面積為小三角形的5倍。則大三角形的邊長

為小三角形對應邊長的√5倍，即大三角形的底為A=√5 a，腰為B=√5×(√5+1)a/2=(√5+5)a/2。

大三角形的腰B與小三角形邊的關係滿足：

B=2a+b

而大三角形的底A與小三角形邊的關係可列舉如下：

2ab

可見大三角形底邊的鄰近區域無法由小三角形不重疊又不超地來填充（圖1）。故命題錯。

另外一種黃金三角形是腰與底的比值為(√5-1)/2的等腰三角形，頂角為108°，底角為36°。

設小三角形的底為a，則腰為b=(√5-1)a/2。

同樣可以證明：

A=2b+a

2b

a

可見大三角形腰的鄰近區域無法由小三角形不重疊又不超出地填充（圖2）。故命題錯。

事實上，勾為a，股為b=2a的直角三角形可以滿足命題要求。

顯然，弦c=√a2+b2 =√5 a

大三角形的對應邊：

A=√5 a=c

B=2A=2c

C=√5×(√5a)=5a=2b+a

滿足上述必要條件。是否成立還要驗證，結果是對的（圖3）。本三角形是否唯一滿足命題還不清楚。

頂角36°的黃金三角形按任意一底角的角平分線分成兩個小等腰三角形，且其中一個等腰三角形的底角是另一個的2倍。頂角是108°的黃金三角形把頂角一個72°和一個36°的角，這條分線也把黃金三角形分成兩個小等腰三角形，且其中一個等腰三角形的底角也是另一個的2倍。

黃金矩形

---

（1）軀體輪廓：肩寬與臀寬的平均數為寬，肩峰至臀底的高度為長；

（2）面部輪廓：眼水平線的面寬為寬，髮際至頦底間距為長；

（3）鼻部輪廓：鼻翼為寬，鼻根至鼻底間距為長；

（4）唇部輪廓：靜止狀態時上下唇峰間距為寬，口角間距為長；

（5）（6）手部輪廓：手的橫徑為寬，五指併攏時取平均數為長；

（7）（8）（9）（10）（11）（12）上頜切牙、側切牙、尖牙（左右各三個）輪廓：最大的近遠中徑為寬，齒齦徑為長。

概述

---

人體中的黃金數

令人驚訝的是，人體自身也和0.618密切相關。對人體解剖很有研究的義大利畫家達·芬奇發現，人的肚臍位於身長的0.618處。科學家們還發現，當外界環境溫度為人體溫度的0.618倍時，人會感到最舒服。

（1）反映鼻口關係的鼻唇指數：鼻翼寬與口角間距之比近似黃金數；

反映眼口關係的目唇指數：口角間距與兩眼外眥間距之比近似黃金數。0.618，作為一個人體健美的標準尺度之一，是無可非議的，但不能忽視其存在著“模糊特性”，它同其它美學參數一樣，都有一個允許變化的幅度，受種族、地域、個體差異的制約。

（2）比例關係 是用數字來表示人體美，並根據一定的基準進行比較。用同一人體的某一部位作為基準，來判定它與人體的比例關係的方法被稱為同身方法。分為三組：係數法，常指頭高身長指數，如畫人體有坐五、立七，即身高在坐位時為頭高的五倍、立位時為7或7.5倍；百分數法，將身長視為100%，身體各部位在其中的比例；兩分法：即把人體分成大小兩部分，大的部分從腳到臍，小的部分為臍到頭頂。標準的面型，其長寬比例協調，符合三停五眼（見右圖）。三停是指臉型的長度，從頭部髮際到下頦的距離分為三等分，即從髮際到眉、眉到鼻尖、鼻尖到下頦各分為一等分，各稱一停共三停；五眼是指臉型的寬度，雙耳間正面投影的長度為五隻眼裂的長度，除眼裂外、內此間距為一眼裂長度、兩側外眥角到耳部各有一眼裂長度，其是五眼長度稱五眼。

（3）角度關係 從不同的角度觀察，所反映的人體形態也各不相同。Belt和Campen等人提出的側角學說，就是通過角度來體現人體形體美的。其中Campen的學說是以鼻下點與耳孔點的直線連線為基準，來測量側面觀察時額頭的傾斜角度的方法，這樣可以把複雜的立體感的頭部，用簡單的輪廓線進行描述－被稱為側面定性分析方法。用連接鼻尖點和頦下點的直線來觀察唇的突出度，評價面下部的美醜。鼻尖、下唇紅前緣、頦下點在同一條直線上，稱為Ricketts美學平面，是一種美的標誌。

黃金點

（1）肚臍：頭頂－足底之分割點；

（2）咽喉：頭頂－肚臍之分割點；

（3）膝關節：肚臍－足底之分割點；

（4）肘關節：肩關節－中指尖之分割點；

（5）乳頭：軀幹乳頭縱軸上這分割點；

（6）眉間點：髮際－頦底間距上1/3與中下2/3之分割點；

（7）鼻下點：髮際－頦底間距下1/3與上中2/3之分割點；

（8）唇珠點：鼻底－頦底間距上1/3與中下2/3之分割點；

（9）頦唇溝正路點：鼻底－頦底間距下1/3與上中2/3之分割點；

（10）左口角點：口裂水平線左1/3與右2/3之分割點；

（11）右口角點：口裂水平線右1/3與左2/3之分割點。面部黃金分割律 面部三庭五眼

（12）左肩關節：左手中指尖-右肩關節之分割點

（13）右肩關節：右手中指尖-左肩關節之分割點

植物中的黃金數

研究發現植物中也蘊涵著黃金數。

植物葉子，千姿百態，生機盎然，給大自然帶來了美麗的綠色世界。儘管葉子形狀隨種而異，但它在莖上的排列順序(稱為葉序)，卻是極有規律的。

你從植物莖的頂端向下看，經細心觀察，發現上下層中相鄰的兩片葉子之間約成137.5°角。如果每層葉子只畫一片來代表，第一層和第二層的相鄰兩葉之間的角度差約是137.5°，以後二到三層，三到四層，四到五層……兩葉之間都成這個角度數。植物學家經過計算表明：這個角度對葉子的採光、通風都是最佳的。葉子的排布，多麼精巧！

葉子間的137.5°角中，藏有什麼“密碼”呢？我們知道，一周是 360°，

360°-137.5°=222.5°

137．5°：222.5°≈0.618。

瞧，這就是“密碼”！葉子的精巧而神奇的排布中，竟然隱藏著0.618。

有些植物的花瓣及主幹上枝條的生長，也是符合這個規律的。

美學中的黃金數

19世紀中葉，德國心理學家費希納曾經做過一次別出心裁的試驗。他召開一次“矩形展覽會”，會上展出了他精心製作的各種矩形，並要求參觀者投票選擇各自認為最美的矩形。結果以下四種矩形入選：

矩形 長×寬 寬與長之比

1．8×5 5:8=0.625

2．13×8 8:13=0.615

3．21×13 13:21=0.619

4．34×21 21:34=0.618

有趣的是，所得的四個矩形的長與寬，它們的比都接近於0.618。

在音樂中，樂曲的高潮一般也在全曲的0.618的位置。

應用

---

由於這樣得出的0.618有許多極為寶貴的性質，因此，人們珍惜地稱它為黃金數，稱點C為黃金分割點，稱這種分割為黃金分割。

黃金數0.618，如今已越來越多地被人們所認識，並被人們所利用。

▲古希臘帕台農神廟由於高和寬的比是0.618，成了舉世聞名的完美建築。建築師們發現，按這樣的比例來設計殿堂，殿堂更加雄偉、壯麗；去設計別墅，別墅將更加舒適、美麗。連一扇門窗若設計為黃金矩形都會顯得更加協調和令人賞心悅目。

▲高雅的藝術殿堂里，自然也留下了黃金數的足跡。畫家們發現，按0.618∶1來設計腿長與身高的比例，畫出的人體身材最優美，而現今的女性，腰身以下的長度平均只佔身高的0.58，因此古希臘維納斯女塑像及太陽神阿波羅的形象都通過故意延長雙腿，使之與身高的比值為0.618，從而創造藝術美。難怪許多姑娘都願意穿上高跟鞋，而芭蕾舞演員則在翩翩起舞時，不時地踮起腳尖。

▲音樂家發現，二胡演奏中，千金分弦的比符合0.618∶1時，奏出來的音調最和諧、最悅耳。

▲只要留心，到處都可發現黃金數這位美的“使者”的足跡。運用於科學實驗和工農業生產的優選法中的0.618法，還能給我們帶來巨大的經濟效益呢！黃金數0.618，真是一件造福人類的絢麗瑰寶！

▲希臘古城雅典有一座用大理石砌成的神廟，神廟大殿中央的女神像是用象牙和黃金雕成的。女神的體態輕柔優美，引人入勝。經專家研究發現，她的身體從腳跟到肚臍間的距離與整個身高的比值，恰好是0.618。不僅雅典娜女神身材如此美好，其他許多希臘女神的身體比例也是如此。人們所熟悉的米洛斯維納斯，太陽神阿波羅的形象，海姑娘阿曼等一些名垂千古的雕像，都可以找到0.618的比值。

▲1483年左右，達芬奇畫的一副未完成的油畫，包圍著聖傑羅姆軀體的黑線，就是一個黃金分割的矩形，當時達芬奇似乎有意利用這一黃金分割的比值。《檢閱》是法國印象派畫家舍勒特的一副油畫，它的畫杠結構比例也正是0.618的比值。英國畫家斐拉克曼在名著《希臘的神話和傳說》一書中，工繪有96幅美人圖。每一幅畫上的美人都嫵媚無比婀娜多姿。如果仔細量一下她們的比例也都與雅典娜相似。

▲中國最古老的古琴，處處透著黃金分割的神奇，琴背兩池，左龍右鳳。控制琴弦發音的樞紐有三：軫，鳧掌，鳳嗉。琴有五弦，音有八度，琴節為徽。“以琴長全體三分損一，又三分益一，而轉相增減”，全弦共有十三徽。把這些排列到一起，二池，三紐，五弦，八音，十三徽。多麼奇妙的排列，恰是費波那奇數，而兩個相鄰斐波那契數列比率則越來越接近黃金分割率，是有意還是巧合？看來，中國古人對黃金分割的領悟與運用，與西方確有異曲同工之妙。

▲早在公元前五世紀，希臘建築家就知道0.618的比值是協調，平衡的結構。古埃及的金字塔，形似方錐，大小各異。但這些金字塔底面的邊長與高之比都接近於0.618。古時候的一些神廟，在建築時高和寬也是按黃金數的比來建立，他們認為這樣的長方形看來是較美觀。黃金律是建築藝術必須遵循的規律。在建築造型上，人們在高塔的黃金分割點處建樓閣或設計平台，便能使平直單調的塔身變得豐富多彩。

▲如果市場上有的電視屏幕主要有兩種，一種是寬：長為3∶4的，另一種是9∶16的。這兩個比值都很接近0.618，也就是因為黃金矩形是最美的。

▲黃金數還運用於化學製藥中。如合成藥物，不知道它在0~100℃之間的哪一個溫度製得合成率最高，藥效最好。很顯然，一個個溫度去試是不實際的。如果運用黃金數就簡單多了。