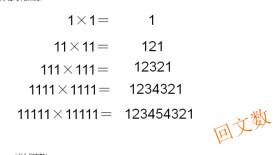迴文數

迴文數是指一個像16461這樣“對稱”的數，即：將這個數的數字按相反的順序重新排列后，所得到的數和原來的數一樣。這裡，“迴文”是指像“媽媽愛我，我愛媽媽”這樣的，正讀反讀都相同的單詞或句子。

迴文數在休閑數學領域備受關注。一個典型的問題就是，尋找那些具有某種特性，並且符合迴文特徵的數。例如：

迴文素數：2, 3, 5, 7, 11, 101, 131, 151,… A002385迴文完全平方數：0, 1, 4, 9, 121, 484, 676, 10201, 12321,… A002779

Buckminster Fuller（Buckminster Fuller）在其著作《協同學》（Synergetics）中把迴文數也叫做沙拉扎數（Scheherazade Numbers），沙拉扎是《一千零一夜》中那位講故事的王妃、即宰相的女兒的名字。

直觀地，在任意的基下都存在著無窮多個迴文數。可以這樣說明：在任意的基下，一個象101, 1001, 10001,… （即由一個1後接n個0再後接一個1）這樣的數可組成一個無窮多項的序列，其各項全部都是迴文數，因此這個基下的迴文數有無窮多個（其中包括但不限於該序列中的無窮多個項）。

10基數下，所有單個數字{0、1、2、3、4、5、6、7、8、9}都是迴文數。

兩位數的迴文數有9個：

{11, 22, 33, 44, 55, 66, 77, 88, 99}.

三位數中有90個迴文數：

{101, 111, 121, 131, 141,151, 161, 171, 181, 191, ..., 909, 919, 929, 939, 949, 959, 969, 979, 989, 999}

四位數中也有90個迴文數：

{1001, 1111, 1221, 1331, 1441, 1551, 1661, 1771, 1881, 1991, ..., 9009, 9119, 9229, 9339, 9449, 9559, 9669, 9779, 9889, 9999},

因此總共有199個小於104的迴文數。小於105的迴文數有1099個，對其它的10的整數冪10n來說，分別有：1998, 10998, 19998, 109998, 199998, 1099998, ... （OEIS中的數列A070199）個迴文數。

也可在十進位以外的其它數系中考慮迴文數。例如，在二進位中的迴文數有：

0, 1, 11, 101, 111, 1001, 1111, 10001, 10101, 11011, 11111, 100001,…

以上這些數在十進位中即：0, 1, 3, 5, 7, 9, 15, 17, 21, 27, 31, 33,…（OEIS中的數列A006995）。梅森素數構成了二進位迴文素數的一個子集。

通常在一個基數下的迴文數在另一個基數下就不再是迴文數。例如：。（下標的數字錶示的是基數，即n16表示以十六進位寫出的n）。然而，有些數字在幾個基數中都是迴文數（稱為“協迴文的”，copalindromic），例如10510在五個不同的基數下都是迴文數：；十進位數1991在十六進位中為7C7，也是迴文的。

在以18為基時，7的一些冪是迴文的：

對任意數n，在所有的基數b下都是迴文的（因為這時n是一個單位數）；在基為時同樣也是迴文數（因為這時n就成了）。如果對於，某數在基b下都是非迴文數，則稱其是一個嚴格非迴文數（Strictly non-palindromic number）。例如6在二進位是110，三進位是20，四進位是12，都不是迴文數，因此它是嚴格非迴文數。這樣的數其中一個特質是6以上的數都是質數。首幾項：1, 2, 3, 4, 6, 11, 19, 47, 53, 79, 103, ... (OEIS:A016038)

在自然數中，最小的迴文數是0，其次是

1,2,3,4,5,6,7,8,9,11,22,33,44,55,66,77,88,99,101,111,121,131,141,151,161,171,181,191,202,212,222,232,242,252,262,272,282,292,303,313,323,333,343,353,363,373,383,393,404,414,424,434,444,454,464,474,484,494,505,515,525,535,545,555,565,575,585,595,606,616,626,636,646,656,666,676,686,696,707,717,727,737,747,757,767,777,787,797,808,818,828,838,848,858,868,878,888,898,909,919,929,939,949,959,969,979,989,999.

定義：一個迴文數，它同時還是某一個數的平方，這樣的數字叫做平方回數。例如：121。

100以上至1000以內的平方回數只有3個，分別是：121、484、676。

其中，121是11的平方。

484是22的平方，同時還是121的4倍。

676是26的平方，同時還是169的4倍。

任意某一個數通過以下方式相加也可得到

如：還有 ，，

不過很多數還沒有發現此類特徵（比如196,下面會講到）

另外個別平方數是迴文數

。。。。

依次類推

上面這些算式，等號左邊是兩個(或三個)因數相乘，右邊是它們的乘積。如果把每個算式中的“×”和“=”去掉，那麼，它們都變成迴文數，所以，我們不妨把這些算式叫做“迴文算式”。還有一些迴文算式，等號兩邊各有兩個因數。請看：

不知你是否注意到，如果分別把上面的迴文算式等號兩邊的因數交換位置，得到的仍是一個迴文算式，比如：分別把“1”等號兩邊的因數交換位置，得到算式是：

這仍是一個迴文算式。

還有更奇妙的迴文算式，請看：

（積是2772）

（積是48384）

這種迴文算式，連乘積都是迴文數。

四位的迴文數有一個特點，就是它決不會是一個質數。設它為abba，那它等於，。能被11整除。

六位的也一樣，也能被11整除

還有，人們藉助電子計算機發現，在完全平方數、完全立方數中的迴文數，其比例要比一般自然數中迴文數所佔的比例大得多。例如，，,，……都是迴文數。

人們迄今未能找到五次方，以及更高次冪的迴文數。於是數學家們猜想：不存在(;n、k均是自然數)形式的迴文數。

在電子計算器的實踐中，還發現了一樁趣事：任何一個自然數與它的倒序數相加，所得的和再與和的倒序數相加，……如此反覆進行下去，經過有限次步驟后，最後必定能得到一個迴文數。

這也僅僅是個猜想，因為有些數並不“馴服”。比如說196這個數，按照上述變換規則重複了數十萬次，仍未得到迴文數。但是人們既不能肯定運算下去永遠得不到迴文數，也不知道需要再運算多少步才能最終得到迴文數。

for '這裡從100開始 後面可以隨便填，我這裡填99999 表示所有3位數到五位數之間的迴文數

if StrReverse(i)=i then print i '用StrReverse函數 判斷倒序后的數和原來數是否相同，如果相同者表示此數為迴文數

next

上而提到的196這個數，是第一個可能的“利克瑞爾數”，因而它受到了最多的關注。由於還不可能證明一個數永遠不能形成“迴文數”，所以“196和其他那些(看起來)不能形成迴文數的數是利克瑞爾數”這一命題僅是猜想而非已獲證明。能證明的僅是那些反例，即如果一個數最終能形成“迴文數”，則它不是“利克瑞爾數”。

在電子計算機尚未問世的1938年，美國數學家萊默(D. Lehmer,1905-1991)計算到了第73步，得到了一個沒有形成“迴文數”的35位的和數。至今挑戰此題的數學愛好者從沒有間斷過，並隨著計算機科技的發展，不斷有發燒友編寫不同的程序對此題發起挑戰。據筆者最新調查，領軍人W.V.Landingham到2006年2月已經計算到了699萬步，得到了一個2.89億位以上的和數，之間的結果仍未出現“迴文數”。

另外介紹一個關於達到“迴文數”需要計算步數的世界記錄。它是一個19位數字1,186,060,307,891,929,990,算出“迴文數，，需要了261步。它是由Jason Doucette的演演算法及程序於2005年11月30日發現的。下表列舉的是各位數字中，到達“迴文數”花費步數最多的代表性數字。

隨意找一個十進位的數，把它倒過來成另一個數，再把這兩個數相加，得一個和數，這是第一步;然後把這個和數倒過來，與原來的和數相加，又得到一個新的和數，這是第二步。照此方法，一步步接續往下算，直到出現一個“迴文數”為n。例如:,，兩步就得出了一個“迴文數”。如果接著算下去，還會得到更多的“迴文數”。這個過程稱為“196演演算法”。

11 is Plalindrome number

123 is not Plalindrome number

17251 is not Plalindrome number

2882 is Plalindrome number

用visual basic6.0

for '這裡從100開始 後面可以隨便填，我這裡填99999 表示所有3位數到五位數之間的迴文數

if StrReverse(i)=i then print i '用StrReverse函數 判斷倒序后的數和原來數是否相同，如果相同者表示此數為迴文數

next

另外一種實現方法（c++）更簡便

#include

using namespace std;

bool symm(long m)

{

long temp = m,n=0;

while (temp)

{

n = n*10+temp%10;

temp = temp/10;

}

return (m == n);

}

int main(int argc, _TCHAR* argv[])

{

long m;

cout<<"請輸入一個整數：";

cin>>m;

cout<<"輸入了"<

return 0;

}

python源程序

1 2	#coding:--utf-8--　#-*-coding:cp936-*- classHws:　def__init__(self):　self.result=[]　defhWs(self):　forainrange(1,10000):　b=str(a)　foriinrange(0,len(b)/2+1):　ifb[i]==b[len(b)-i-1]:　self.result.append(a)　printself.result　hws=Hws()　hws.hWs()

求最長迴文數長度的manacher演演算法（O(n)）

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

#include #include #include #include #include #include #include #include #include #defineINF99999999 usingnamespacestd;   constintMAX=110000+10; chars[MAX*2]; intp[MAX*2];   intmain(){ while(scanf("%s",s)!=EOF){ intlen=strlen(s),id=0,maxlen=0; for(inti=len;i>=0;--i){//插入'#' s[i+i+2]=s[i]; s[i+i+1]='#'; }//插入了len+1個'#',最終的s長度是1~len+len+1即2*len+1,首尾s[0]和s[2*len+2]要插入不同的字元 s[0]='*';//s[0]='*',s[len+len+2]='\0',防止在while時p[i]越界 for(inti=2;i<2*len+1;++i){ if(p[id]+id>i)p[i]=min(p[2*id-i],p[id]+id-i); elsep[i]=1; while(s[i-p[i]]==s[i+p[i]])++p[i]; if(id+p[id] if(maxlen } cout< } return0; }