同倫群
同倫群
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。
同倫群(homotopy groups)基本群的高維推廣。基本群是從單位閉區間I到拓撲空間X的閉路的同倫等價類和其運算得到的。
基本群亦稱一維同倫群。對一個拓撲空間聯繫一個群的代數結構。
同倫群
同倫群
同倫群
是 的邊界,即:
同倫群
同倫群
同倫群
設X為拓撲空間,x∈X,用M(X,x)表示全體連續映射α:( , )→(X,x)所成的集合,α和α′相對於I的同倫關係αα′是M(X,x)上的一個等價關係,它把M(X,x)的元素分成一些同倫等價類,用π(X,x)表示這些等價類所成的集合。定義映射α*β:(I,I)→(X,x),使得:
同倫群
同倫群
同倫群
同倫群
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。
設G為一個非空集合,a、b、c為它的任意元素。如果對G所定義的一種代數運算“·”(稱為“乘法”,運算結果稱為“乘積”)滿足:
(1)封閉性,a·b∈G;
(2)結合律,即(a·b)c = a·(b·c);
(3)對G中任意元素a、b,在G中存在惟一的元素x,y,使得a·x= b,y·a=b,則稱G對於所定義的運算“·”構成一個群。例如,所有不等於零的實數,關於通常的乘法構成一個群;時針轉動(關於模12加法),構成一個群。
滿足交換律的群,稱為交換群。
群是數學最重要的概念之一,已滲透到現代數學的所有分支及其他學科中。凡是涉及對稱,就存在群。例如,可以用研究圖形在變換群下保持不變的性質,來定義各種幾何學,即利用變換群對幾何學進行分類。可以說,不了解群,就不可能理解現代數學。
基本群亦稱一維同倫群。對一個拓撲空間聯繫一個群的代數結構。在拓撲空間X中對於以同一點x為基點的兩條閉道路α和β可引入乘法*:
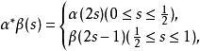
同倫群
[α]°[β]=[α*β],
這種定義是有意義的,並且以x為基點的全體閉路同倫類在引入這種乘法后構成一群,稱為X的以x為基點的基本群,記為π(X,x).基本群可以不是交換群。對於道路連通空間X,其基本群與基點的選取無關,記為π(X).對於兩個拓撲空間X與Y之間的連續映射f:(X,p)→(Y,q),它與X內以p為基點的閉路α的複合映射f°α是Y內以q為基點的閉路,並且兩條同倫的閉路與f的複合得出兩條同倫的閉路,因此,按照f([α])=[f°α]定義映射:
f: π(X,p)→π(Y,q),
於是f為同態,稱為f誘導的同態。由此得出基本群是拓撲不變數,進而基本群也是同倫型不變數。
計算基本群常常是將所討論的空間“歸結”或“分解”為更簡單的空間以算出其基本群,這些常見的方法有:
1.利用基本群的同倫型不變性.
同倫群
3.利用覆疊空間理論.
4.利用范卡彭定理:若K是連通的復形,K,K,K都是K的連通的子復形,使得
同倫群
