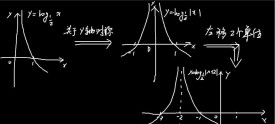
對數變換

如果a(a>0，且a≠1)的b次冪等於N，即ab=N，那麼數b叫做以a為底N的對數，記作：logan=b,其中a叫做對數的底數，N叫做真數.

由定義知：

①負數和零沒有對數;

②a>0且a≠1,N>0;

③loga1=0,logaa=1,alogaN=N,logaab=b.

特別地，以10為底的對數叫常用對數，記作log10N,簡記為lgN；以無理數e(e=2.71828…)為底的對數叫做自然對數，記作logeN，簡記為lnN.

對數式與指數式的互化式子名稱abN指數式ab=N(底數)(指數)(冪值)對數式logaN=b(底數)(對數)(真數)

如果a>0,a≠1,M>0,N>0,那麼

(1)loga(MN)=logaM+logaN.

(2)logaMN=logaM-logaN.

(3)logaMn=nlogaM(n∈R).

問：①公式中為什麼要加條件a>0,a≠1，M>0,N>0?

②logaan=?(n∈R)

③對數式與指數式的比較.(學生填表)

式子ab=NlogaN=b名稱a—冪的底數

b—N—a—對數的底數

b—N—運算性質

am·an=am+n

am÷an=(am)n=(a>0且a≠1,n∈R)logaMN=logaM+logaN

logaMN=logaMn=(n∈R)

(a>0,a≠1,M>0,N>0)

對數定義中，為什麼要規定a＞0,，且a≠1?

理由如下：

①若a＜0，則N的某些值不存在，例如log-28

②若a=0，則N≠0時b不存在；N=0時b不惟一，可以為任何正數

③若a=1時，則N≠1時b不存在；N=1時b也不惟一，可以為任何正數

為了避免上述各種情況，所以規定對數式的底是一個不等於1的正數

1.(1)將下列指數式寫成對數式：

①54=625；②2-6=164；③3x=27；④13m=5.73

（2）將下列對數式寫成指數式：

①log1216=-4；②log2128=7；

③log327=x；④lg0.01=-2；

⑤ln10=2.303；⑥lgπ=k.

解析由對數定義：ab=NlogaN=b.

解答

(1)①log5625=4.

②log2164=-6.

③log327=x

.④log135.73=m.

解題方法

指數式與對數式的互化，必須並且只需緊緊抓住對數的定義：ab=NlogaN=b.(2)①12-4=16.②27=128.③3x=27.

④10-2=0.01.⑤e2.303=10.⑥10k=π.

2.根據下列條件分別求x的值：

(1)log8x=-23；(2)log2(log5x)=0；

(3)logx27=31+log32；(4)logx(2+3)=-1.

解析(1)對數式化指數式，得：x=8-23=?

(2)log5x=20=1.x=?

(3)31+log32=3×3log32=?27=x?

(4)2+3=x-1=1x.x=?

解答(1)x=8-23=(23)-23=2-2=14.

(2)log5x=20=1，x=51=5.

(3)logx27=3×3log32=3×2=6，

∴x6=27=33=(3)6,故x=3.

(4)2+3=x-1=1x,∴x=12+3=2-3.

①轉化的思想是一個重要的數學思想，對數式與指數式有著密切的關係，在解決有關問題時，經常進行著兩種形式的相互轉化.

②熟練應用公式：loga1=0,logaa=1,alogaM=M,logaan=n.3

已知logax=4,logay=5，求A=〔x·3x-1y2〕12的值.

解析思路一，已知對數式的值，要求指數式的值，可將對數式轉化為指數式，再利用指數式的運算求值；思路二，對指數式的兩邊取同底的對數，再利用對數式的運算求值

解答解法一∵logax=4,logay=5,

∴x=a4,y=a5,

∴A=x512y-13=(a4)512(a5)-13=a53·a-53=a0=1.

解法二對所求指數式兩邊取以a為底的對數得

logaA=loga(x512y-13)

=512logax-13logay=512×4-13×5=0,

∴A=1.

有時對數運算比指數運算來得方便，因此以指數形式出現的式子，可利用取對數的方法，把指數運算轉化為對數運算.

4設x,y均為正數，且x·y1+LGX=1(x≠110),求lg(xy)的取值範圍.

解析一個等式中含兩個變數x、y，對每一個確定的正數x由等式都有惟一的正數y與之對應，故y是x的函數，從而lg(xy)也是x的函數。因此求lg(xy)的取值範圍實際上是一個求函數值域的問題，怎樣才能建立這種函數關係呢？能否對已知的等式兩邊也取對數?

解答∵x>0,y>0,x·y1+lgx=1,

兩邊取對數得：lgx+(1+lgx)lgy=0.

即lgy=-lgx1+lgx(x≠110,lgx≠-1).

令lgx=t,則lgy=-t1+t(t≠-1).

∴lg(xy)=lgx+lgy=t-t1+t=T21+t.

對一個等式兩邊取對數是解決含有指數式和對數式問題的常用的有效方法；而變數替換可把較複雜問題轉化為較簡單的問題。設S=t21+t,得關於t的方程t2-St-S=0有實數解.

∴Δ=S2+4S≥0，解得S≤-4或S≥0,

故lg(xy)的取值範圍是(-∞,-4〕∪〔0,+∞).

5求值：

(1)lg25+lg2·lg50+(lg2)2；

(2)2log32-log3329+log38-52log53；

(3)設lga+lgb=2lg(a-2b)，求log2a-log2b的值;

(4)求7lg20·12lg0.7的值.

解析(1)25=52,50=5×10.都化成lg2與lg5的關係式.

(2)轉化為log32的關係式.

(3)所求log2a-log2b=log2ab由已知等式給出了a,b之間的關係，能否從中求出ab的值呢?

(4)7lg20·12lg0.7是兩個指數冪的乘積，且指數含常用對數，

設x=7lg20·12lg0.7能否先求出lgx，再求x?

解答(1)原式=lg52+lg2·lg(10×5)+(lg2)2

=2lg5+lg2·(1+lg5)+(lg2)2

=lg5·(2+lg2)+lg2+(lg2)2

=lg102·(2+lg2)+lg2+(lg2)2

=(1-lg2)(2+lg2)+lg2+(lg2)2

=2-lg2-(lg2)2+lg2+(lg2)2=2.

(2)原式=2log32-(log325-log332)+log323-5log59

=2log32-5log32+2+3log32-9

=-7.

(3)由已知lgab=lg(a-2b)2(a-2b>0),

∴ab=(a-2b)2,即a2-5ab+4b2=0.

∴ab=1或ab=4，這裡a>0,b>0.

若ab=1，則a-2b0,a≠1,c>0,c≠1,N>0)；

(2)logab·logbc=logac；

(3)logab=1logba(b>0,b≠1)；

(4)loganbm=mnlogab.

解析(1)設logaN=b得ab=N,兩邊取以c為底的對數求出b就可能得證.

(2)中logbc能否也換成以a為底的對數.

(3)應用(1)將logab換成以b為底的對數.

(4)應用(1)將loganbm換成以a為底的對數.

解答(1)設logaN=b，則ab=N,兩邊取以c為底的對數得：b·logca=logcN,

∴b=logcNlogca.∴logaN=logcNlogca.

(2)由(1)logbc=logaclogab.

所以logab·logbc=logab·logaclogab=logac.

(3)由(1)logab=logbblogba=1logba.

(1)中logaN=logcNlogca叫做對數換底公式，(2)(3)(4)是(1)的推論，它們在對數運算和含對數的等式證明中經常應用。對於對數的換底公式，既要善於正用，也要善於逆用.(4)由(1)loganbm=logabmlogaan=mlogabnlogaa=mnlogab.

7.已知log67=a,3b=4,求log127.

解析依題意a,b是常數，求log127就是要用a,b表示log127，又3b=4即log34=b，能否將log127轉化為以6為底的對數，進而轉化為以3為底呢?

解答已知log67=a,log34=b,

∴log127=log67log612=a1+log62.

又log62=log32log36=log321+log32,

由log34=b,得2log32=b.

∴log32=b2,∴log62=b21+b2=b2+b.

∴log127=a1+b2+b=a(2+b)2+2b.

利用已知條件求對數的值，一般運用換底公式和對數運演演算法則，把對數用已知條件表示出來，這是常用的方法技巧

8.已知x,y,z∈R+，且3x=4y=6z.

(1)求滿足2x=py的p值；

(2)求與p最接近的整數值；

(3)求證：12y=1z-1x.

解析已知條件中給出了指數冪的連等式，能否引進中間量m，再用m分別表示x,y,z?又想，對於指數式能否用對數的方法去解答?

解答（1）解法一3x=4ylog33x=log34yx=ylog342x=2ylog34=ylog316,

∴p=log316.

解法二設3x=4y=m,取對數得：

x·lg3=lgm，ylg4=lgm,

∴x=lgmlg3,y=lgmlg4,2x=2lgmlg3,py=plgmlg4.

由2y=py,得2lgmlg3=plgmlg4,

∴p=2lg4lg3=lg42lg3=log316.

(2)∵2=log393-p.

∴與p最接近的整數是3.

①提倡一題多解。不同的思路，不同的方法，應用了不同的知識或者是相同知識的靈活運用，既發散了思維，又提高了分析問題和解決問題的能力，何樂而不為呢?

②(2)中涉及比較兩個對數的大小。這是同底的兩個對數比大小。因為底3>1，所以真數大的對數就大，問題轉化為比較兩個真數的大小，這裡超前應用了對數函數的單調性，以鼓勵學生超前學習，自覺學習的學習積極性.(3)解法一令3x=4y=6z=m,由於x，y，z∈R+，

∴k>1，則x=lgmlg3,y=lgmlg4,z=lgmlg6,

所以1z-1x=lg6lgm-lg3lgm=lg6-lg3lgm=lg2lgm，12y=12·lg4lgm=lg2lgm，

故12y=1z-1x.

解法二3x=4y=6z=m，

則有3=m1x①,4=m1y②，6=m1z③，

③÷①，得m1z-1x=63=2=m12y.

∴1z-1x=12y.

9.已知正數a,b滿足a2+b2=7ab.求證：logma+b3=12(logma+logmb)(m>0且m≠1).

解析已知a>0,b>0,a2+b2=7ab.求證式中真數都只含a,b的一次式，想：能否將真數中的一次式也轉化為二次，進而應用a2+b2=7ab?

解答logma+b3=logm(a+b3)212=

①將a+b3向二次轉化以利於應用a2+b2=7ab是技巧之一.

②應用a2+b2=7ab將真數的和式轉化為ab的乘積式，以便於應用對數運算性質是技巧之二.12logma+b32=12logma2+b2+2ab9.

∵a2+b2=7ab,

∴logma+b3=12logm7ab+2ab9=12logmab=12(logma+logmb),

即logma+b3=12(logma+logmb).

1.數學興趣小組專門研究了科學記數法與常用對數間的關係。設真數N=a×10n.其中N>0,1≤a0,lgN的首數和尾數與a×10n有什麼聯繫？

有效數字相同的不同正數其常用對數的什麼相同？什麼不同？

2.若lgx的首數比lg1x的首數大9，lgx的尾數比lg1x的尾數小03804，且lg0.2034=1.3083,求lgx,x,lg1x的值.

解析①lg0.2034=13083,即lg0.2034=1+0.3083，1是對數的首數，0.3083是對數的尾數，是正的純小數；②若設lgx=n+lga，則lg1x也可表出.

解答設lgx=n+lga,依題意lg1x=(n-9)+(lga+0.3804).

又lg1x=-lgx=-(n+lga),

∴(n-9)+(lga+03804)=-n-lga，其中n-9是首數，lga+03804是尾數，-n-lga=-(n+1)+(1-lga),-(n+1)是首數1-lga是尾數，所以：

n-9=-(n+1)

lga+0.3804=1-lgan=4,

lga=0.3083.

∴lgx=4+0.3083=4.3083,

∵lg0.2034=1.3083,∴x=2.034×104.

∴lg1x=-(4+0.3083)=5.6917.

把lgx的首數和尾數，lg1x的首數和尾數都看成未知數，根據題目的等量關係列方程。再由同一對數的首數等於首數，尾數等於尾數，求出未知數的值，是解決這類問題的常用方法.3

計算：

(1)log2-3(2+3)+log6(2+3+2-3);

(2)2lg(lga100)2+lg(lga).

解析(1)中.2+3與2-3有何關係?2+3+2-3雙重根號，如何化簡?

(2)中分母已無法化簡，分子能化簡嗎?

解題方法

認真審題、理解題意、抓住特點、找出明確的解題思路和方法，不要被表面的繁、難所嚇倒。解答(1)原式=log2-3(2-3）-1+12log6(2+3+2-3)2

=-1+12log6(4+22+3·2-3)

=-1+12log66

=-12.

(2)原式=2lg(100lga)2+lg(lga)=2〔lg100+lg(lga)〕2+lg(lga)=2〔2+lg(lga)〕2+lg(lga)=2.

4

已知log2x=log3y=log5z55.

∴550,b>0,M≠1),且logMb=x，則logMa的值為()

A若log63=0.6731，log6x=-0.3269,則x為()

A若log5〔log3(log2x)〕=0，則x=.

9.8log87·log76·log65=.

10如果方程lg2x+(lg2+lg3)lgx+lg2·lg3=0的兩根為x1、x2,那麼x1·x2的值為.

11生態學指出：生物系統中，每輸入一個營養級的能量，大約只有10%的能量流到下一個營養級.H1→H2→H3→H4→H5→H6這條生物鏈中(Hn表示第n個營養級，n=1，2，3，4，5，6).已知對H1輸入了106千焦的能量，問第幾個營養級能獲得100千焦的能量?

12已知x，y，z∈R+且3x=4y=6z，比較3x，4y，6z的大小.

13已知a,b均為不等於1的正數，且axby=aybx=1，求證x2=y2.

14已知2a·5b=2c·5d=10，證明(a-1)(d-1)=(b-1)(c-1).

15設集合M=｛x|lg〔ax2-2(a+1)x-1〕>0｝，若M≠，M｛x|x0且x+1≠1;真數x+1>0.

6.A點撥：對ab=M取以M為底的對數.

7.C點撥：注意0.6731+0.3269=1,log61x=0.3269，

所以log63+log61x=log63x=1.∴3x=6,x=12.

8.x=8點撥：由外向內.log3(log2x)=1,log2x=3,x=23.

9.5點撥：log87·log76·log65=log85,8log85=5.

10.16點撥：關於lgx的一元二次方程的兩根是lgx1,lgx2.

由lgx1=-lg2,lgx2=-lg3，得x1=12,x2=13.

11.設第n個營養級能獲得100千焦的能量，

依題意:106·10100n-1=100,

化簡得:107-n=102,利用同底冪相等，得7-n=2,

或者兩邊取常用對數也得7-n=2.

∴n=5,即第5個營養級能獲能量100千焦.

12設3x=4y=6z=k,因為x，y，z∈R+，

所以k>1.取以k為底的對數，得：

x=1logk3,y=1logk4,z=1logk6.

∴3x=3logk3=113logk3=1logk33,

同理得：4y=1logk44,6z=1logk66.

而33=1281,44=1264,66=1236,

∴logk33>logk44>logk66.

又k>1,33>44>66>1,

∴logk33>logk44>logk66>0,∴3x0),則

ax2-2(a+1)x-1=10t(t>0).

∴10t>1,ax2-2(a+1)x-1>1,∴ax2-2(a+1)x-2>0.

①當a=0時，解集｛x|x0時,M=｛x|xx2｝,顯然不是｛x|x0，

x1+x2=2(a+1)a0.

解得3-2<0，綜上所求，A的取值範圍是：3-2

16.N=3.840×1011,lgN=11.5843.

17.設經過x年，成本降為原來的40%.則

(1-10%)x=40%,兩邊取常用對數，得：

x·lg(1-10%)=lg40%，

即x=lg0.4lg0.9=lg4-1lg9-1=2lg2-12lg3-1=10.

所以經過10年成本降低為原來的40%.

18.f(x)=log1.104x〔或f(x)=lgxlg1.104〕.

點撥：設原來一個季度產品為a，則a(1+10.4%)y=xa,∴y=log1.104x.