量子電動力學
量子場論中的分支之一
量子電動力學(Quantum Electrodynamics,英文簡寫為QED)是量子場論中最成熟的一個分支。它研究的對象是電磁相互作用的量子性質(即光子的發射和吸收)、帶電粒子的產生和湮沒、帶電粒子間的散射、帶電粒子與光子間的散射等等。它概括了原子物理、分子物理、固體物理、核物理和粒子物理各個領域中的電磁相互作用的基本原理。
量創久,...狄、..海森伯和W,泡利於1929年相繼提出了輻射的量子理論,奠定了量子電動力學的理論基礎。在量子力學範圍內,可以把帶電粒子與電磁場相互作用當作微擾,來處理光的吸收和受激發射問題,但卻不能處理光的自發射問題。因為如果把電磁場作為經典場看待,在發射光子以前根本不存在輻射場。原子中處於激發態的電子是量子力學中的定態,沒有輻射場作為微擾,它就不會發生躍遷。自發射是確定存在的事實,為了解釋這種現象並定量地給出它的發生幾率,在量子力學中只能用變通的辦法來處理。一個辦法是利用對應原理,把原子中處於激發態的電子看成是許多諧振子的總和,把產生輻射的振蕩電流認定與量子力學的某些躍遷矩陣元相對應,用以計算自發射的躍遷幾率。從這個處理辦法可以得到M.普朗克的輻射公式,以此反過來說明對應原理的處理是可行的。另外一種辦法是利用A.愛因斯坦關於自發射幾率和吸收幾率間的關係。雖然這些辦法所得的結果可以和實驗結果符合,但在理論上究竟是與量子力學體系相矛盾的──量子力學的定態壽命為無限大。
驗提挑。,狄拉克相對論波動方程對描述電子行為是十分成功的:它能預指出電子自旋為1/2,磁矩(稱為玻爾磁子),所給出的氫原子能級和實驗也符合得較好。由於實驗技術的迅速發展,更精確的測量給出氫原子的2P1/2和2S1/2態能量稍有差別,而狄拉克方程給出這兩個狀態能量相同。這個差別稱為蘭姆移位。另外,電子磁矩也略偏離於一個玻爾磁子。在此以前曾考慮過,電子是要和電磁輻射場的真空漲落相互作用的。但計算這種相互作用能遇到了發散困難,因此被擱置起來。在確切的實驗結果面前,就非解決不可了。蘭姆移位發現后一年,H.A.貝特就作了一個估算。他考慮處於2S1/2和2P1/2態的電子和真空漲落的相互作用能雖然都是無限大,但經過一些近似處理它們的差可得出有限值,而且和實驗定性符合。於是如何從無限大中分出有意義的有限部分就成為一系列新的計算的共同指導思想,雖然這些嘗試都還比較成功,但它們都有一個共同的問題:從無限大分出有意義的有限結果的過程都很繁瑣而且不很可靠。因此需要找出明確、簡潔而且在理論上有根據的辦法,它的結果還要和實驗符合。
論系..費曼、..施溫、朝永振一郎、F.J.戴森等人在1948~1949年建立的。他們用“重正化”的概念把發散量確切而不含混地歸入電荷與質量的重新定義之中,從而使高階近似的理論結果都不再包含發散。發散量的處理充分利用了相對論協變性和規範不變性。新理論表述之所以能夠作到確切地處理髮散量,是因為從一開始就把理論表述嚴格地建立在相對論協變形式及規範不變要求的基礎之上。
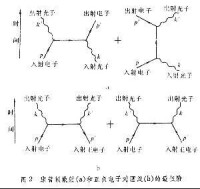
量子電動力學
