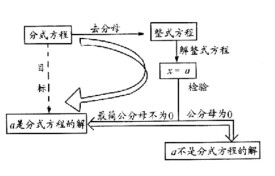
增根

對於分母的值為零時，這個分數無意義，所以不允許分母為0，即本身就隱含著分母不為零的條件。當把分式方程轉化為整式方程以後，這種限制取消了，換言之，方程中未知數的值範圍擴大了，如果轉化后的整式方程的根恰好是原方程未知數的允許值之外的值，那麼就會出現增根。

解：去分母，，

∴。

又因為，

∴方程無解

∴方程無意義，是增根。

設方程是由方程變形得來的，如果這兩個方程的根完全相同（包括重數），那麼稱這兩個方程等價。如果是方程的根但不是的根，稱是方程的增根；如果是方程的根但不是的根，稱是方程的失根。

在兩非函數方程（如圓錐曲線）聯立求解的過程中，增根的出現主要表現在定義域的變化上。

例如：若已知橢圓，O為原點坐標，A為橢圓右頂點，若橢圓上存在一點P，使，求橢圓的圓心率的範圍。

解：橢圓上存在一點P，使，即是以OA為直徑畫圓，要求與橢圓有除了以外的另外一個解。所以聯立橢圓和圓的方程：

因為有兩個根，所以

而正解卻是

由（*）得

∴

∴

然而問題出在，無論怎麼取，只要，好像永遠都大於0。

於是我們取

假設

即可得橢圓···①

與圓···②

聯立即可得···(*)

有十字相乘

顯然此時是增根

將帶入①式

將帶入②式

將帶入(*)式

可知這裡的確是產生了一個增根，而且在解題過程中不能通過任何方式排除，這說明多個非函數方程聯立求解時，方程本身無法限制x的取值。一般來說，直線與圓錐曲線的聯立並沒有出現過算出兩個解，還需要帶回去驗根的情況，大概是因為圓錐曲線不是函數，而直線是函數的原因。

注意：

1.不是任何的兩個非函數方程聯立都會產生增根。例如圓不是函數，但求兩個圓的交點，不會產生增根。

2.增根的產生和定義域有關係，但沒有絕對的關係。不能說聯立方程時，將x定義域擴大或縮小就必然會引起增根。如上述例題中，①式定義域(-2,2)②式定義域(0,2)大多數人是在②式中，用x表示y，寫成，再帶入①式，產生了增根。但是如果我們在①式中用x表示y，寫成，再帶入②式，我們依然會得到增根。

下面列出兩種必然會出現增根的一般式：

橢圓與拋物線增根

橢圓(和拋物線聯立方程式得：

由韋達定理得且

可知，若，則，出現原因是忽略了中的隱含定義域。聯立方程式求解誤認為（另外我們還知道）。

雙曲線與拋物線增根

雙曲線和拋物線聯立方程式得

由韋達定理得且

可知，若，則，出現原因是忽略了中的隱含定義域。聯立方程式求解誤認為（另外我們還知道）。

解：兩邊平方得

得

得或（增根）

出現增根的原因是由於兩邊平方忽略了上式的且根號內的值大於等於0。

由於同樣的粗心大意，錯誤還會在無理不等式中體現。

解分式方程時出現增根或失根，往往是由於違反了方程的同解原理或對方程變形時粗心大意造成的。

如果不遵從同解原理，即使解整式方程也可能出現增根．例如將方程的兩邊都乘x，變形成，方程兩邊所乘的最簡公分母，看其是否為0，是0即為增根。

還可以把x代入最簡公分母也可。

增根的產生，歸根結底都是因為思維的不全面產生的。解題時要保證步步變形的等價性，這種等價性要通過等式和不等式去約束出來，特別是不等式，容易被忽略。如果不得已必須用不等價變形來解題，那麼最後千萬別忘記通過檢驗來去掉增根，這種檢驗也要注意全面性。

許多人解方程時，得到了增根，比如說能量是負值，一般的人都會將這個忽視掉，但這些值是挺令人尋味的。著名的物理學家狄拉克利用相對論、量子力學尋找粒子的能量時，他發現某個粒子的能量和其動量緊密相關，即（p為動量，m為粒子的質量），解得,你肯定想保留正根，因為你知道能量不會是負值，但數學家們告訴狄拉克，你不能忽略負值，因為數學告訴我有兩個根，你不能隨便丟掉。

後來事實證明，第二個根，也就是為負的那個根，正是理論的關鍵：世界上既有粒子，也有反粒子。負能量就是用來解釋什麼是反粒子的。